Eccentric dipole: Formulas of Hurwitz (1960)
Geomagnetic field is usually described by combination of a geocentric dipole field and higher order nondipole fields. As this is mathematical convenience, it is also possible to describe the field by a single eccentric dipole. For accurate description of the geomagnetic field, it is useful to determine the Gauss coefficients raised by dipole offset for not only low degree terms but also those of high degrees. Hurwitz (1960) presented formulas to calculate them for any high orders. Hurwitz's paper is very concise, making it difficult to understand the theory for those who are not very good at mathematics. The following explanation is based on Sanoo (2000).
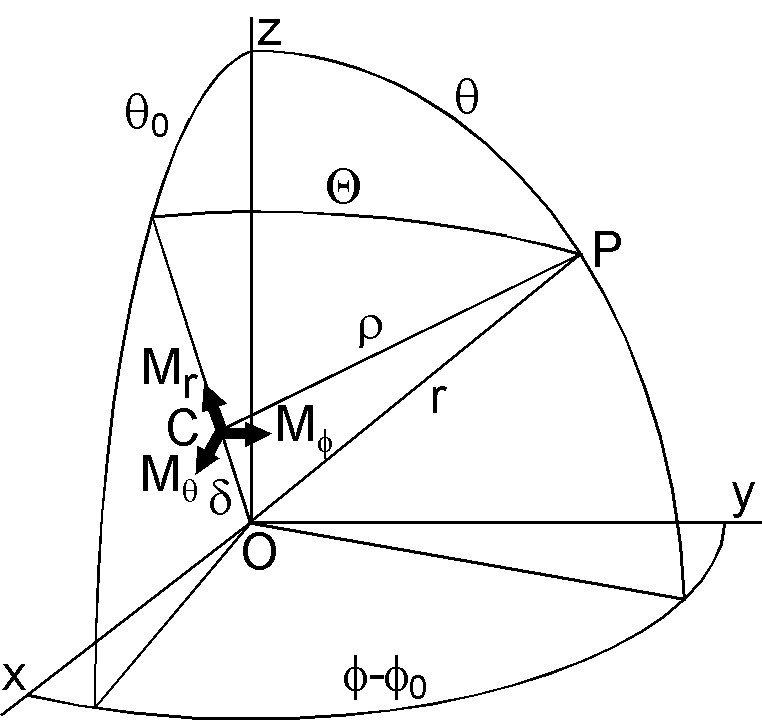
Suppose there is a dipole \({\bf M}=(M_x,M_y,M_z)\) at the earth's center O. Now, this dipole is displaced to a point C \((x_c,y_c,z_c)\) while its orientation is unchanged. We introduce a vector \(\boldsymbol{\delta}=(x_c,y_c,z_c)\) for the displacement \(\overrightarrow{\mathsf{OC}}\), which is denoted in spherical coordinates as \((\delta,\theta_0,\phi_0)\). We also introduce an observation point P \((r,\theta,\phi,)\), a vector \(\boldsymbol{\rho}\) for \(\overrightarrow{\mathsf{CP}}\), and \(\Theta\) for an angle \(\angle\mathsf{COP}\).
The three components of the eccentric dipole in orthogonal coordinates, \((M_x,M_y,M_z)\), are unchanged wherever it is placed, but those in spherical coordinates, \((M_r,M_\theta,M_\phi)\), are dependent on \(\boldsymbol{\delta}\). They are related through a rotation matrix of coordinates axes as shown below; \begin{equation} \left(\begin{array}{c} M_\theta \\ M_\phi \\ M_r \end{array}\right) = \left(\begin{array}{ccc} \cos\phi_0\cos\theta_0 & \sin\phi_0\cos\theta_0 & -\sin\theta_0 \\ \label{eq01} -\sin\phi_0 & \cos\phi_0 & 0 \\ \cos\phi_0\sin\theta_0 & \sin\phi_0\sin\theta_0 & \cos\theta_0 \end{array}\right) \left(\begin{array}{c} M_x \\ M_y \\ M_z \end{array}\right) \end{equation}
Now the potential \(W\) at P is given by sum of three potentials, \begin{equation} W = W_r + W_\theta + W_\phi, \label{eq02} \end{equation} where \(W_r\), \(W_\theta\), and \(W_\phi\) are those caused by \({\bf M_r}\), \({\bf M}_\boldsymbol{\theta}\), and \({\bf M}_\boldsymbol{\phi}\), respectively. Potential \(W_r\) is expressed as, \[ W_r = \frac{\mu_0}{4\pi}\frac{{\bf M_r}\cdot\boldsymbol{\rho}}{\rho^3} = \frac{\mu_0}{4\pi}\frac{{\bf M_r}\cdot({\bf r} - \boldsymbol{\delta})}{\rho^3} = \frac{\mu_0}{4\pi}\frac{M_r r\cos\Theta -M_r\delta}{\rho^3}. \] Using the next relation for \(\cos\Theta\), \begin{equation} \cos\Theta = \cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0), \label{eq03} \end{equation} \(W_r\) becomes, \begin{equation} W_r = \frac{\mu_0}{4\pi}\frac{M_r r\left(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0) - \frac{\delta}{r}\right)}{\rho^3}. \label{eq04} \end{equation} For \(W_\theta\), denoting the angle between \({\bf M}_\boldsymbol{\theta}\) and \({\bf r}\) as \(\Theta'\), \(\cos\Theta'\) is obtained by replacing \(\theta_0\) by \(\theta_0+\pi/2\) in \eqref{eq03}. Hence, \(W_\theta\) becomes, \begin{equation} W_\theta = \frac{\mu_0}{4\pi}\frac{M_\theta r\left(-\cos\theta\sin\theta_0 + \sin\theta\cos\theta_0\cos(\phi-\phi_0)\right)}{\rho^3}. \label{eq05} \end{equation} Similarly, \(W_\phi\) is given by, \begin{equation} W_\phi = \frac{\mu_0}{4\pi}\frac{M_\phi r\sin\theta\sin(\phi-\phi_0)}{\rho^3}. \label{eq06} \end{equation}
We introduce two distance variables normalized by \(r\), \begin{equation} \xi = \frac{\rho}{r}, \qquad h = \frac{\delta}{r}. \label{eq07} \end{equation} Then it is easy to show that the potentials are given by the following equations. \begin{eqnarray} W_r & = & \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\partial}{\partial h}\left(\frac{1}{\xi}\right), \label{eq08} \\ W_\theta & = & \frac{\mu_0}{4\pi}\frac{M_\theta}{r^2}\frac{1}{h}\frac{\partial}{\partial\theta_0}\left(\frac{1}{\xi}\right), \label{eq09} \\ W_\phi & = & \frac{\mu_0}{4\pi}\frac{M_\phi}{r^2}\frac{1}{h\sin\theta_0}\frac{\partial}{\partial\phi_0}\left(\frac{1}{\xi}\right). \label{eq10} \end{eqnarray} To ascertain \eqref{eq08}, using the definitions of \eqref{eq07}, \(\xi\) is given by, \begin{eqnarray*} \xi & = & \rho/r = \left.\sqrt{r^2 - 2r\delta\cos\Theta + \delta^2}\right/r, \\ & = & \sqrt{1 - 2h(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0)) + h^2}. \end{eqnarray*} Partially differentiating \(1/\xi\) by \(h\), \begin{eqnarray*} \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\partial}{\partial h}\left(\frac{1}{\xi}\right) & = & -\frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{1}{\xi^2}\frac{\partial \xi}{\partial h} \\ & = &\frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0) - h}{\xi^3} \\ & = & \frac{\mu_0}{4\pi}\frac{M_r r\left(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0) - \frac{\delta}{r}\right)}{\rho^3}, \end{eqnarray*} which is the equation \eqref{eq04}. Similarly, equivalence of \eqref{eq09} to \eqref{eq05}, and \eqref{eq10} to \eqref{eq06} is ascertained.
Lastly, we use two equations of Legendre polynomials; generating function, \[ \frac{1}{\xi} = \frac{1}{\sqrt{1 - 2\cos\Theta h + h^2}} = \sum_{n=0}^\infty P_n(\cos\Theta)h^n, \] and addition theorem, \begin{eqnarray*} P_n(\cos\Theta) & = & P_n(\cos\theta\cos\theta_0 + \sin\theta\sin\theta_0\cos(\phi-\phi_0)), \\ & = & \sum_{m=0}^n P_n^m(\cos\theta)P_n^m(\cos\theta_0)\cos m(\phi-\phi_0). \end{eqnarray*} Substituting these equations to \eqref{eq08}, \begin{eqnarray*} W_r & = & \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\frac{\partial}{\partial h}\sum_{n=0}^\infty\sum_{m=0}^n P_n^m(\cos\theta)P_n^m(\cos\theta_0)\cos m(\phi-\phi_0) h^n, \\ & = & \frac{\mu_0}{4\pi}\frac{M_r}{r^2}\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{\delta}{r}\right)^{n-1}n P_n^m(\cos\theta_0) \\ & & \times(\cos m\phi_0 \cos m\phi + \sin m\phi_0 \sin m\phi)P_n^m(\cos\theta), \\ & = & a\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\frac{\mu_0 M_r}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}n P_n^m(\cos\theta_0) \\ & & \times(\cos m\phi_0 \cos m\phi + \sin m\phi_0 \sin m\phi)P_n^m(\cos\theta). \end{eqnarray*} Hence, the Gauss coefficients for \(W_r\) are given by, \begin{equation} {g_r}_n^m = \frac{\mu_0 M_r}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}n P_n^m(\cos\theta_0)\cos m\phi_0, \quad {h_r}_n^m = {g_r}_n^m \tan m\phi_0. \label{eq11} \end{equation} Similarly, \(W_\theta\) of \eqref{eq09} becomes, \begin{eqnarray*} W_\theta & = & a\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\frac{\mu_0 M_\theta}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{d P_n^m(\cos\theta_0)}{d\theta_0} \\ & & \times(\cos m\phi_0 \cos m\phi + \sin m\phi_0 \sin m\phi)P_n^m(\cos\theta), \end{eqnarray*} and the Gauss coefficients for \(W_\theta\) are given by, \begin{equation} {g_\theta}_n^m = \frac{\mu_0 M_\theta}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{d P_n^m(\cos\theta_0)}{d\theta_0}\cos m\phi_0, \quad {h_\theta}_n^m = {g_\theta}_n^m \tan m\phi_0. \label{eq12} \end{equation} \(W_\phi\) of \eqref{eq10} now becomes, \begin{eqnarray*} W_\phi & = & a\sum_{n=0}^\infty\sum_{m=0}^n\left(\frac{a}{r}\right)^{n+1}\frac{\mu_0 M_\phi}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{m}{\sin\theta_0} P_n^m(\cos\theta_0) \\ & & \times(-\sin m\phi_0 \cos m\phi + \cos m\phi_0 \sin m\phi)P_n^m(\cos\theta), \end{eqnarray*} and the Gauss coefficients for \(W_\phi\) are given by, \begin{eqnarray} {g_\phi}_n^m & = & -\frac{\mu_0 M_\phi}{4\pi a^3}\left(\frac{\delta}{a}\right)^{n-1}\frac{m}{\sin\theta_0} P_n^m(\cos\theta_0)\sin m\phi_0, \label{eq13} \\ {h_\phi}_n^m & = & -{g_\phi}_n^m \cot m\phi_0. \nonumber \end{eqnarray}
In summary, the following is the procedure to calculate the Gauss coefficients caused by an eccentric dipole \({\bf M}=(M_x,M_y,M_z)\) placed at C \((x_c,y_c,z_c)\), or \((\delta,\theta_0,\phi_0)\). First transfer \({\bf M}\) to \((M_\theta,M_\phi,M_r)\) using \eqref{eq01} and then calculate the Gauss coefficients for \(W_r\), \(W_\theta\), and \(W_\phi\) by using \eqref{eq11}, \eqref{eq12}, and \eqref{eq13}. Lastly the Gauss coefficients are given by, \[ g_n^m = {g_r}_n^m + {g_\theta}_n^m + {g_\phi}_n^m, \quad h_n^m = {h_r}_n^m + {h_\theta}_n^m + {h_\phi}_n^m. \]
References:
- Hurwitz, L., Eccentric dipoles and spherical harmonic analysis, J. Geophys. Res., 65, 2555-2556, 1960.
- Sanoo, Y., Personal communication, Asahi University, 2000.