(舞台設定)
ψ1(x),ψ2(x):ψ1(x),ψ2(x)は (連続でなくてもよいが)[a,b]上リーマン積分可能な有界関数を表すとする。
また、[a,b]上ψ1(x)≦ψ2(x) が成り立つとする。
A : Aは、R2上の点集合{ (x ,y ) | a≦x≦b, ψ1(x)≦y≦ψ2(x) }
つまり、a≦x≦bの範囲で、ψ1(x)、ψ2(x)に挟まれた範囲
を表すとする。
f(x,y) : ここでは、関数 f (x,y)として、Aの上で定義された有界関数のみを考える。
(本題)
f (x ,y ) がA上リーマン積分可能、
xを固定してyの関数となった f (x ,y )が、
xを[a,b]上のどんな値に固定しても 、[ψ1(x), ψ2(x)]上y方向に可積分、
すなわち、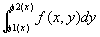 が存在する
が存在する
ならば、
xの[a,b]上の固定位置と、y方向の積分値とを対応付けた関数
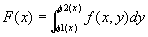
は、[a,b]上可積分となって、
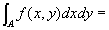
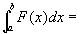
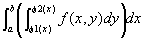
(証明) 杉浦『解析入門I』IV章定理9.8-3(p.271.)
仮定: f (x ,y )がA上リーマン積分可能 …(仮定1)
xを固定してyの関数となった f (x ,y )が、
xを[a,b]上のどんな値に固定しても 、[ψ1(x), ψ2(x)]上y方向に可積分、
すなわち、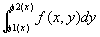 が存在する …(仮定2)
が存在する …(仮定2)
設定:Aを含む閉矩形K={ (x ,y ) | a≦x≦b, c≦y≦d } (c≦ψ1(x)≦ψ2≦d)をひとつとる。
つまり、閉矩形K⊃A (設定1)
(たとえば、下図緑部のように、閉矩形Kをとる)

A上では f (x ,y ) の値をとり、それ以外ではゼロをとる、閉矩形K上の関数f * (x ,y )をつくる。
つまり、f * (x ,y )= f (x ,y ) χA(x ,y ) …(設定2)
本題:
(step1) (仮定1) f (x ,y ) がA上リーマン積分可能とは、定義より、
f * (x ,y )が閉矩形K上リーマン積分可能
となることだった。
(step2) xを固定してyの関数となった f * (x ,y )について考える。
・xを固定してyの関数となったf * (x ,y )は、
xを[a,b]上のどんな値に固定しても 、[ c,ψ1(x)]上リーマン積分可能。
なぜなら、(設定2)より、 c ≦y<ψ1(x)のとき常にf * (x ,y )=0
y=ψ1(x)のときf * (x ,y )= f (x ,y ) だから、
[ c,ψ1(x)]上f * (x ,y )は、y=ψ1(x)の一点を除いて、連続。
よって、定理(閉区間上有限個数の点を除いて連続ならば可積分)より、
f * (x ,y )は [ c,ψ1(x)]上可積分
・xを固定してyの関数となったf * (x ,y )は、
xを[a,b]上のどんな値に固定しても 、[ψ2(x), d ]上でも、リーマン積分可能。
なぜなら、(設定2)より、ψ2(x) <y≦dのとき常にf * (x ,y )=0
y=ψ2(x)のときf * (x ,y )= f (x ,y ) だから、
[ψ2(x), d ]上f * (x ,y )は、y=ψ2(x)の一点を除いて、連続。
よって、定理(閉区間上有限個数の点を除いて連続ならば可積分)より、
f * (x ,y )は [ψ2(x), d ]上リーマン積分可能
・xを固定してyの関数となったf * (x ,y )は、
xを[a,b]上のどんな値に固定しても 、[ψ1(x),ψ2(x) ]上、リーマン積分可能。
なぜなら、ψ1(x)≦y≦ψ2(x)のときf * (x ,y )= f (x ,y ) ∵(設定2)
よって、(仮定2)より、ψ1(x)≦y≦ψ2(x)でf * (x ,y )はリーマン積分可能。
以上3点から、積分の区間加法性が成立し、
xを固定してyの関数となったf * (x ,y )は、
xを[a,b]上のどんな値に固定しても 、
[c,d]上y方向にリーマン積分可能で、…(step2-結論1)
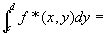
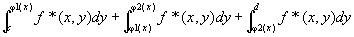
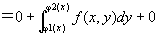
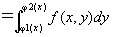 …(step2-結論2)
…(step2-結論2)
(step3) step1での結論と(step2-結論1)から、矩形上の重積分の累次積分への還元可能条件が満たされるので、
xの[a,b]上の固定位置と、y方向の積分値とを対応付けた関数
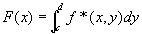
は、[a,b]上可積分となって、
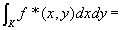
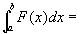
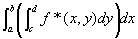
(step4)一般の有界集合上の二重積分の定義を用いてstep3の結論を書きかえると、
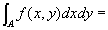
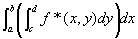
(step5) step4の結論を、(step2-結論2)を用いて書きかえると、
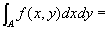
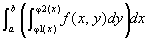
定理:連続曲線で囲まれた集合上での、連続関数の重積分は、累次積分に還元可能
[吹田新保『理工系の微分積分学』196-7;高木『解析概論』8章93節(p.336.);
笠原『微分積分学』7.2節[4]定理7. 20系2(p.264.);黒田『微分積分』10章2節(354-5);
杉浦ほか『解析演習』IV章1.8系(1)(p.274.); Lang, Undergraduate Analysis,Example(486-487.)
和達『微分積分』140-4;。]
(舞台設定)
ψ1(x),ψ2(x):ψ1(x),ψ2(x)は [a,b]上の連続関数を表すとする。
また、[a,b]上ψ1(x)≦ψ2(x) が成り立つとする。
A : Aは、R2上の点集合{ (x ,y ) | a≦x≦b, ψ1(x)≦y≦ψ2(x) }
つまり、a≦x≦bの範囲で、二つの連続曲線ψ1(x)、ψ2(x)に挟まれた範囲
を表すとする。
例1:

例2:

f (x ,y ) : ここでは、関数 f (x ,y )として、Aの上で定義された有界関数のみを考える。
(本題)
〇1 以上の設定下で、Aは面積確定。Aの境界は、面積ゼロ。
以上の設定に付け加えて、 f (x ,y )がA上連続ならば、
〇2 F(x)=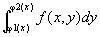
は、[a,b]上の連続関数。 [吹田新保『理工系の微分積分学』196]
〇3 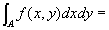
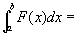
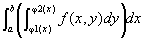 (重積分の累次積分への帰着)
(重積分の累次積分への帰着)
〇4 [吹田新保『理工系の微分積分学』196-7;和達『微分積分』142;。]
積分範囲A={ (x ,y ) | a≦x≦b, ψ1(x)≦y≦ψ2(x) }を、
[c,d]上の連続関数φ1(y)、φ2(y)を用いて、
A={ (x ,y ) | c≦y≦d,φ1(y)≦x≦φ2(y) }
とも表せるならば、
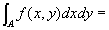
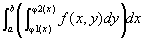
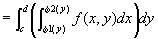 (累次積分の順序変更)
(累次積分の順序変更)
(証明)
〇1 杉浦『解析入門I』IV章定理9.8-1,2(p.271.)を見よ。
まずAの境界の面積がゼロであることを示し、定理を使って、Aの面積確定を導出。
〇2 吹田新保『理工系の微分積分学』196を見よ。
〇3 [高木『解析概論』8章93節(p.336.);]
仮定: f (x ,y ) がA上連続 …(1)
設定:Aを含む閉矩形K={ (x ,y ) | a≦x≦b, c≦y≦d } (c≦ψ1(x)≦ψ2≦d)をひとつとる。
つまり、閉矩形K⊃A …(2)
(たとえば、下図緑部のように、閉矩形Kをとる)

A上では f (x ,y )の値をとり、それ以外ではゼロをとる、閉矩形K上の関数f * (x ,y )をつくる。
つまり、f * (x ,y )= f (x ,y ) χA(x ,y ) …(3)
本題:
(step1) (1)と(3)より、
f * (x ,y ) の不連続点は、Aの境界に限られ、
Aの境界以外の全ての点では、f * (x ,y )は連続。
(step2) 〇1より、Aは面積確定で、Aの境界は面積ゼロ。
だから、閉矩形K上のf * (x ,y )の不連続点の集合は面積ゼロとなり、
定理より、f * (x ,y )は閉矩形K上リーマン積分可能となる。
(step3) xを固定してyの関数となった f * (x ,y )について考える。
(3)より、
ψ2(x) <y≦dのときf * (x ,y )=0,
ψ1(x)≦y≦ψ2(x)のときf * (x ,y )= f (x ,y )
c ≦y<ψ1(x)のときf * (x ,y )=0
定理より、2変数について連続ならば、そこで各変数についても連続となるので、
step1より、xを固定してyの関数となった f * (x ,y ) の不連続点は、Aの境界に限られ、
Aの境界以外の全ての点では、f * (x ,y )は連続。
xを固定してyの関数となった f * (x ,y ) にとっては、xを[a,b]上のどんな値に固定しても 、
Aの境界=不連続点は、ψ1(x),ψ2(x)の2点にすぎない。
よって、定理より、xを固定してyの関数となったf * (x ,y )は、
xを[a,b]上のどんな値に固定しても 、[c,d]上y方向に可積分。
(step4) step2,3の結果から、矩形上の重積分の累次積分への還元可能条件が満たされるので、
xの[a,b]上の固定位置と、y方向の積分値とを対応付けた関数
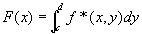
は、[a,b]上可積分となって、
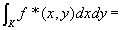
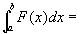
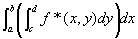
(step5)一般の有界集合上の二重積分の定義を用いてstep4の結論を書きかえると、
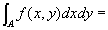
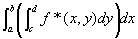
(step6) 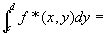
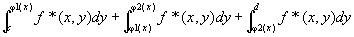 ∵区間加法性
∵区間加法性
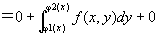
∵ y<ψ1(x)のときf * (x ,y )=0、
ψ1(x)≦y≦ψ2(x)のときf * (x ,y )= f (x ,y )
y>ψ2 (x)のときf * (x ,y )=0
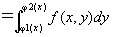
となることを用いて、step5の結論を書きかえると、
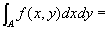
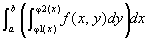
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、202項積分法(pp.520-525)→リーマン積分、
杉浦光夫『解析入門I』東京大学出版会、1980年、IV章§9(pp.270-275.) n変数関数全般について。
杉浦光夫ほか『解析演習』東京大学出版会、1989年、IV章1.7-1.8(pp.273-275.)証明ナシ。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年、pp.196-7.
高木貞治『解析概論:改訂第3版』岩波書店、1983年、8章93節(p.336.)
笠原皓司『微分積分学』サイエンス社、1974年、7.2節[4]定理7.19 -20(pp.262-4.)。
黒田成俊『21世紀の数学1:微分積分』共立出版、2002年、第10章2節(p. 354.)。
Lang,Serge.Undergraduate Analysis(Undergraduate
Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg
Tokyo,1983,Chapter 19. Multiple Integrals. (pp.468-482.)。
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp. 140-4;
小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、87-89. アイデアだけ。厳密な議論なし。



