順序と順序集合の定義
[トピック一覧:順序・順序集合の定義]
・順序の公理(順序・順序集合)、全順序・全順序集合、狭義順序、部分順序集合
・順序同型写像・順序同型
※順序集合関連ページ:順序集合のの諸概念(最大最小・極大極小・上界下界・上限sup下限inf)、
双対順序・双対順序集合・双対概念・自己双対的・双対命題・双対原理
整列順序・整列順序集合、整列定理・ツォルンの補題
→
参考文献・総目次
順序の公理:
(半)順序(semi/ partial)order・順序関係order relation、(半)順序集合(semi/ partially) ordered set
[斎藤『数学の基礎:集合・数・位相』1章§3順序1.3.1(p.21); 松坂『集合・位相入門』第3章§1-A;B(p.87);
『岩波数学辞典(第三版)』項目168.順序 (pp.440-1).神谷・浦井『経済学のための数学入門』2.1.1節定義2.1.1(p.57).]
(設定)
X: 集合
x,y : Xの元
R(x,y):X上の2項関係
(本題)
X上の2項関係R(x,y)が
1.反射律reflexive law: 任意のx ∈Xについて、R(x, x )
2.反対称律antisymmetric law: 任意のx ,y ∈Xについて、R(x,y) かつR(y, x) ならば、x=y
※むしろ、この対偶
「任意のx ,y ∈Xについて、
x≠yならば、
R(x,y)と R(y, x)のいずれかであって、両方は同時に成り立たない。」
のほうが、「反対称律」という名称になじむ。
3.推移律transitive law: 任意のx, y,z ∈Xについて、P (x, y)かつP (y,z) ならば、P (x,z)である。
を満たすとき、
X上の2項関係R(x,y)を、X上の(半)順序関係・(半)順序(ブルバキ的には順序「構造」)といい、
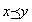
と表す。
順序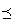 が定義された集合Xを、台集合・台とよび、
が定義された集合Xを、台集合・台とよび、
台集合Xと順序の組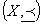 を、(半)順序集合と呼ぶが、省略して、「順序集合X」などということもある。
を、(半)順序集合と呼ぶが、省略して、「順序集合X」などということもある。
※このように、順序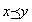 は定義されるので、順序が定義されたところでは必ず、以下が成り立つ。
は定義されるので、順序が定義されたところでは必ず、以下が成り立つ。
1.反射律: 任意のx ∈Xについて、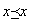
2.反対称律: 任意のx ,y ∈Xについて、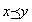 かつ
かつ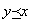 ならば、x=y
ならば、x=y
※むしろ、この対偶
「任意のx ,y ∈Xについて、
x≠yならば、
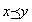 か
か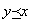 のいずれかであって、両方は同時に成り立たない。」
のいずれかであって、両方は同時に成り立たない。」
のほうが、「反対称律」という名称になじむ。
3.推移律transitive law: 任意のx, y,z ∈Xについて、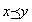 かつ
かつ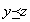 ならば、
ならば、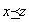 である。
である。
※狭義順序<は、上記の順序≦から、派生的に定義される。→狭義順序<
※順序集合の例:
・自然数上の大小関係"≦"は、順序の3条件を満たす、したがって、自然数と"≦"の組は順序集合。
・実数上の大小関係"≦"は、順序の3条件を満たす、したがって、実数と"≦"の組はは順序集合。
・集合Xのべき集合上P(X)上で、集合Xの部分集合間の包含関係"⊂"は順序の3条件を満たし、
したがって、P(X)と"⊂"の組は順序集合。
[斎藤『数学の基礎:集合・数・位相』第1章§3順序1.3.2-2(p.21); 松坂『集合・位相入門』第3章§1-A(p.88);]
※
下位類型:全順序・全順序集合、整列順序・整列集合
→
[トピック一覧:順序・順序集合の定義]
→
総目次
定義:
全順序total order、線形順序linear order、全順序集合totally ordered set,linearly ordered set
[斎藤『数学の基礎:集合・数・位相』第1章§3順序1.3.1(p.21);松坂『集合・位相入門』第3章§1-A;B(pp.87-9);
『岩波数学辞典(第三版)』項目168.順序 (pp.440-1).神谷・浦井『経済学のための数学入門』2.1.1節定義2.1.1(p.57).]
(設定)
X: 集合
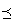 :X上の順序関係
:X上の順序関係
 :順序集合
:順序集合
(本題)
Xの任意の元x,yについて、
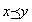 または
または 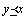 の少なくともいずれか一方が成立するとき、
の少なくともいずれか一方が成立するとき、
X上の順序関係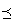 をとくに、全順序・線形順序とよび、
をとくに、全順序・線形順序とよび、
順序集合 を、全順序集合・線形順序集合とよぶ。
を、全順序集合・線形順序集合とよぶ。
※全順序集合の例:
・自然数上の大小関係"≦"は、全順序の定義を満たす、したがって、自然数と"≦"の組は全順序集合。
・実数上の大小関係"≦"は、全順序の定義を満たす、したがって、実数と"≦"の組は全順序集合。
※上位類型:順序・順序集合
※下位類型:順序環・順序体
→
[トピック一覧:順序・順序集合の定義]
→
総目次
定義:
狭義順序
[斎藤『数学の基礎:集合・数・位相』第1章§3順序1.3.1(p.22);]
(設定)
X: 集合
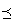 :X上の順序関係
:X上の順序関係
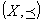 :順序集合
:順序集合
(本題)
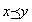 かつx≠yを、x<yとかくと、
かつx≠yを、x<yとかくと、
以下が満たされる。
1. 任意のx∈Xにたいして、 x< xではない
2. 任意のx,y∈Xにたいして、x < y かつ y < xということはない。
3. 任意のx,y,z∈Xにたいして、x < y かつ y < zならば、x < z
この関係"<"を狭義順序という。
→
[トピック一覧:順序・順序集合の定義]
→
総目次
定義:
部分順序集合
[松坂『集合・位相入門』第3章§1-B(p.89);]
(設定)
X: 集合
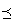 :X上の順序関係
:X上の順序関係
 :順序集合
:順序集合
A : Xの部分集合。ただし空集合ではないとする。つまり、A⊂XかつA≠φ
(本題)
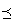 は、X上の順序関係だから、定義より、
は、X上の順序関係だから、定義より、
Xの任意の元について、反射律・反対称律・推移律が満たされている。
したがって、Xの部分集合Aの任意の元についても、反射律・反対称律・推移律が満たされるから、
Aの任意の元a,bに対して、
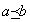 ⇔
⇔ 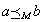
として、M上の順序関係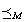 を定義できる。
を定義できる。
このようにしてつくった順序集合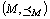 を、順序集合
を、順序集合 の部分順序集合という。
の部分順序集合という。
また、通常、M上の順序関係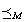 を単に
を単に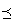 と書く。
と書く。
→
[トピック一覧:順序・順序集合の定義]
→
総目次
定義:
順序同型写像order isomorphism、順序同型 order isomorphic
[斎藤『数学の基礎:集合・数・位相』第1章§3順序1.3.1(p.22); ; 松坂『集合・位相入門』第3章§1-D(p.94);
『岩波数学辞典(第三版)』項目168.順序E (p.441).]
(設定)
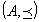 : 順序集合
: 順序集合
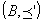 : 順序集合
: 順序集合
f:AからBへの全単射(双射)
(本題)
・fがAからBへの順序同型写像であるとは、
任意のx,y∈Aに対して、
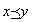 ならば、
ならば、 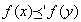
かつ
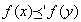 ならば、
ならば、 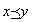
が成り立つことをいう。
・AからBへの順序同型写像が存在するとき、AとBは順序同型であるといい、
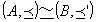
などと表す。
※
関連概念:代数としての同型、順序環・順序体における同型
→
[トピック一覧:順序・順序集合の定義]
→
総目次
(
reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目156A.実数の公理系 (pp. 417-418), 168.順序 (pp.440-441).
[集合論についてのテキスト]
斎藤正彦『数学の基礎:集合・数・位相』東大出版会、2002年。第1章§3順序(pp.21-33)。
松坂和夫『集合・位相入門』岩波書店、1968年、第3章§1順序集合(pp.87-96)
ブルバキ『数学原論・集合論・要約』東京図書、1968年、§6順序集合(pp.36-43)。
[解析学についてのテキスト]
高木貞二『解析概論改訂第三版』岩波書店、1983年、pp.1-5.
杉浦光夫『解析入門I』岩波書店、1980年、pp.1-9.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ−ルタ−・ルディン『現代解析学』共立出版、1971年、第1章。
Колмогоров и Фомин, Элементы Теории Функций и Функционального Анализа =コルモゴロフ・フォミーン(山崎三郎訳)『函数解析の基礎第2版』岩波書店、1971年。第1章§4全順序集合、超限数。
[数理経済学についてのテキスト]
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.56-64