双対順序・双対原理
[トピック一覧：双対順序・双対原理]
・双対順序･双対順序集合、双対概念、自己双対的、双対命題、双対原理　
※順序集合関連ページ：順序と順序集合の定義　
　　　　　　　　　　　順序集合上の諸概念(最大最小･極大極小･上界下界・上限sup下限inf)、
　　　　　　　　　　　整列順序・整列順序集合、整列定理･ツォルンの補題　　

→参考文献・総目次

定義：双対順序、双対順序集合　　
[松坂『集合･位相入門』第3章§１-E(p.96);『岩波数学辞典（第三版）』項目168.順序Ａ (p.440)..]
（設定）
X:　集合
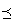：X上の順序関係
：順序集合
（本題）
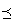・の双対順序とは、
　　　　集合Xの任意の元x,yについて、　 ⇔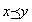 　
　として定義されたX上の2項関係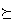のこと。
・の双対順序集合とは、
　集合Xと、「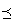の 双対順序 」である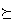との組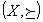のことをいう。

定義：双対概念　
[松坂『集合･位相入門』第3章§１-E(p.96);『岩波数学辞典（第三版）』項目168.順序Ａ (p.440)..]
双対概念とは、双対順序を考えるときに互いに入れ替わる概念のこと。
（例）
最大元と最小元は、互いの双対概念。
上限と下限は、互いの双対概念。

→[トピック一覧：双対順序・双対原理]
→総目次

定義：自己双対的な概念　
[松坂『集合･位相入門』第3章§１-E(p.96);『岩波数学辞典（第三版）』項目168.順序Ａ (p.440)..]
自己双対的な概念とは、その双対概念と論理的に同等な概念のこと。

→[トピック一覧：双対順序・双対原理]
→総目次

定義：双対命題　
[松坂『集合･位相入門』第3章§１-E(p.96);『岩波数学辞典（第三版）』項目168.順序Ａ (p.440)..]
・命題Pの双対命題とは、
　　命題Pのなかに現れる順序に関する概念を、それぞれその双対概念で置き換えてえられる命題のこと。
・順序集合において命題Pが成り立つならば、
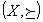　　の双対順序集合において、命題Pの双対命題が成り立つ。

→[トピック一覧：双対順序・双対原理]
→総目次

定理：双対原理duality principle　　
[松坂『集合･位相入門』第3章§１-E(p.96);『岩波数学辞典（第三版）』項目168.順序Ａ (p.440)..]
順序にかかわる条件Cを満たす限りで任意の順序集合において命題Pが成り立つならば、
条件Cの双対命題を満たす限りで任意の双対順序集合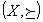において、
命題Pの双対命題が成り立つ。

→[トピック一覧：双対順序・双対原理]
→総目次

（reference）
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目156Ａ.実数の公理系 (pp. 417-418), 168.順序 (pp.440-441).
[集合論についてのテキスト]
斎藤正彦『数学の基礎：集合・数・位相』東大出版会、2002年。第1章§３順序(pp.21-33)。
松坂和夫『集合・位相入門』岩波書店、1968年、第3章§１順序集合(pp.87-96)
ブルバキ『数学原論・集合論・要約』東京図書、1968年、§6順序集合(pp.36-43)。
[解析学についてのテキスト]
高木貞二『解析概論改訂第三版』岩波書店、1983年、pp.1-5.
杉浦光夫『解析入門I』岩波書店、1980年、pp.1-9.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ−ルタ−・ルディン『現代解析学』共立出版、1971年、第1章。
[数理経済学についてのテキスト]
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.56-64

→[トピック一覧：双対順序・双対原理]
→総目次