整列順序
well-order・整列順序集合・整列集合
[トピック一覧：整列順序・整列集合]
・定義：極小条件、極大条件、整列順序･整列集合、切片、逆整列集合
・定理：超限帰納法
※順序集合関連ページ：順序と順序集合の定義
順序集合の諸概念(最大最小･極大極小･上界下界・上限sup下限inf)、
双対順序･双対順序集合･双対概念･自己双対的･双対命題･双対原理
→
参考文献・総目次
定義：
極小条件minimal condition
[『岩波数学辞典（第三版）』項目168.順序C (p.441).]
（設定）
: 順序集合
（本題）
Xが極小条件minimal conditionを満足するとは、
空集合を除く、Xのあらゆる部分集合が最小元をもつことをいう。
※極小条件の双対概念：極大条件
定義：
極大条件maximal conditon
[『岩波数学辞典（第三版）』項目168.順序C (p.441).]
（設定）
: 順序集合
（本題）
Xが極大条件maximal conditionを満足するとは、
空集合を除く、Xのあらゆる部分集合が最大元をもつことをいう。
※極大条件の双対概念：極小条件
定義：
整列順序well-order・整列順序集合・整列集合well-ordered set
[斎藤『数学の基礎：集合・数・位相』第1章§３順序1.3.19(p.30); ; 松坂『集合・位相入門』第3章§2-A(p.98);
『岩波数学辞典（第三版）』項目168.順序C (p.441).]
（設定）
: 順序集合
（本題）
順序集合が整列順序集合・整列集合であるとは、
Xが極小条件を満足すること
つまり、空集合を除く、Xのあらゆる部分集合が最小元をもつこと
をいう。
順序集合が整列順序集合・整列集合であときの順序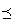
を整列順序と呼ぶ。
順序集合が整列順序集合・整列集合であることを、
「Xは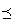によって整列されている」ともいう。
※整列集合の双対概念：逆整列集合
※整列集合の具体例：自然数
※上位概念：順序・順序集合
→
[トピック一覧：整列順序・整列集合]
→
総目次
定義：
切片 segment, Abschnitt
[松坂『集合・位相入門』第3章§2-B(p.99);『岩波数学辞典（第三版）』項目168.順序B (p.440).]
（設定）
: 整列集合
（本題）
「Xのa∈Xによる切片」とは、
{x|x∈X かつ x<a}
のこと。
→
[トピック一覧：整列順序・整列集合]
→
総目次
定義：
逆整列集合inversely well-ordered set
[『岩波数学辞典（第三版）』項目168.順序C (p.441).]
（設定）
: 順序集合
（本題）
順序集合が逆整列集合であるとは、
Xが極大条件を満足すること
つまり、空集合を除く、Xのあらゆる部分集合が最大元をもつこと
をいう。
※逆整列集合のの双対概念：整列集合
→
[トピック一覧：整列順序・整列集合]
→
総目次
定理：
超限帰納法transfinite induction
[松坂『集合・位相入門』第3章§2-B定理2(p.100);『岩波数学辞典（第三版）』項目168.順序C (p.441).]
（設定）
: 整列集合
（本題）
整列集合の元に関する命題Pについて、次の条件が示されるならば、
命題Pは整列集合のすべての元について成り立つ。
条件： aを X の任意の元とする。
x<aを満たす限りで任意のx∈X について、命題Pが成り立つならば、
命題Pはa∈Xについても成り立つ
→
[トピック一覧：整列順序・整列集合]
→
総目次
（
reference）
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目156Ａ.実数の公理系 (pp. 417-418), 168.順序 (pp.440-441).
[集合論についてのテキスト]
斎藤正彦『数学の基礎：集合・数・位相』東大出版会、2002年。第1章§３順序(pp.21-33)。
松坂和夫『集合・位相入門』岩波書店、1968年、第3章§１順序集合(pp.87-96)
ブルバキ『数学原論・集合論・要約』東京図書、1968年、§6順序集合(pp.36-43)。
[解析学についてのテキスト]
高木貞二『解析概論改訂第三版』岩波書店、1983年、pp.1-5.
杉浦光夫『解析入門I』岩波書店、1980年、pp.1-9.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ−ルタ−・ルディン『現代解析学』共立出版、1971年、第1章。
[数理経済学についてのテキスト]
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.56-64
→
[トピック一覧：整列順序・整列集合]
→
総目次