[トピック一覧：順序のついた代数系]
　定義：順序環、順序体　　
　定理：順序体の自己稠密性　　
※代数系関連ページ―代数系の諸概念：代数系、同型　　
※代数系関連ページ−ほかの代数系：半群、群、環、体
※関連ページ：順序･順序集合

→代数系目次・総目次・参照文献

定義：順序環　
　[斉藤『数学の基礎：集合・数・位相』2章§1定義2.1.1 (p.38);『岩波数学辞典』項目121構造C代数系(p.327);]
（設定）
X:　集合
x+y：X上の加法　
xy ：X上の乗法　
X:　　加法x+y, 乗法xyという二つの二項演算を、集合X に定めてつくった代数系。
　　※代数系を、もとの集合X 自体とは別の記号で表したほうが正確なのだろうが、慣例に従う。　　
（定義）
順序環とは、
　加法x+y, 乗法xyという二つの二項演算を、集合X に定めてつくった様々な代数系Xのなかでも特に、
　次の4条件を満たす代数系Xのことをいう。
　条件A. Xが環であること。
　条件B. X上に全順序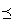が定義されており、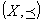が全順序集合であること。
　　　なお、ここから、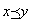かつx≠yを、狭義順序x<yと定義する。　　
　条件C. X上に定められた加法と狭義順序が以下を満たすこと。
　　　( ∀x, y, z ∈X ) ( x < y ⇒ x + z < y+ z )　　　
　条件D. X上に定められた乗法と狭義順序が以下を満たすこと。
　　　( ∀x, y, z ∈X ) ( x < y かつ 0 < z ⇒ xz < yz , zx < zy )　　
※ 代数系Xが条件A-Cを満たすならば、条件Dと次の条件D'は同値であるから、
　　条件Dを、条件D'に置換えてもよい。
　　条件D'. X上に定められた乗法と狭義順序が以下を満たすこと。
　　　　( ∀x, y∈X ) ( 0< x かつ 0 < y ⇒ 0< xy )　
　　証明→斉藤『数学の基礎：集合・数・位相』2章§1問題4 (p.39);略解(p.249);　　
　　　
（例）　　
　整数の集合。　　　　　　
　　　　　　　

→[トピック一覧：順序のついた代数系]
→代数系目次・総目次　

定義：順序体　ordered field　　
　[斉藤『数学の基礎：集合・数・位相』2章§1定義2.1.1 (p.38);『岩波数学辞典』項目229体N(p.645);]
（設定）
X:　集合
x+y：X上の加法　
xy ：X上の乗法　
X:　　加法x+y, 乗法xyという二つの二項演算を、集合X に定めてつくった代数系。
　　※代数系を、もとの集合X 自体とは別の記号で表したほうが正確なのだろうが、慣例に従う。　　
（定義）
順序体とは、
　加法x+y, 乗法xyという二つの二項演算を、集合X に定めてつくった様々な代数系Xのなかでも特に、
　次の4条件を満たす代数系Xのことをいう。
　条件A. Xが体であること。
　条件B. X上に全順序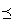が定義されており、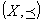が全順序集合であること。
　　　なお、ここから、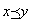かつx≠yを、狭義順序x<yと定義する。　　
　条件C. X上に定められた加法と狭義順序が以下を満たすこと。
　　　( ∀x, y, z ∈X ) ( x < y ⇒ x + z < y+ z )　　　
　条件D. X上に定められた乗法と狭義順序が以下を満たすこと。
　　　( ∀x, y, z ∈X ) ( x < y かつ 0 < z ⇒ xz < yz )　　　
※ 代数系Xが条件A-Cを満たすならば、条件Dと次の条件D'は同値であるから、
　　条件Dを、条件D'に置換えてもよい。
　　条件D'. X上に定められた乗法と狭義順序が以下を満たすこと。
　　　　( ∀x, y∈X ) ( 0< x かつ 0 < y ⇒ 0< xy )　
　　証明→斉藤『数学の基礎：集合・数・位相』2章§1問題4 (p.39);略解(p.249);　　
※条件C-Dから、順序体の自己稠密性が導出される。　　
（例）　　
　有理数の集合。　　　　　　
　実数体。　　　　　　

→[トピック一覧：順序のついた代数系]
→代数系目次・総目次　

定理：順序体の自己稠密性
　[斉藤『数学の基礎：集合・数・位相』2章§5定義2.5.1 (p.52);赤『実数論講義』§2.7(pp.54-5);]
順序体は、自己稠密である。
すなわち、
　順序体Kの任意の元x,yにたいして、x<z<yを満たすKの元zが存在する。
　すなわち、(∃z∈K) (∀x,y∈K) ( x<z<y )
（証明）
順序体の条件C,Dから。
詳しくは、赤『実数論講義』§2.7(pp.54-5)。
　

定義：順序同型写像　　　　
（設定）
X ,Y:　順序環もしくは順序体　　
（定義）
XからYへの順序同型写像とは、
　　1. XからYへの代数系としての同型写像
　　かつ　　　
　　2. XからYへの順序集合としての順序同型写像　
　である全単射(双射) f ：X→Yのことをいう。

→[トピック一覧：順序のついた代数系]
→代数系目次・総目次　

日本数学会編集『岩波数学辞典(第3版)』 岩波書店、1985年、項目121構造A構造2)算法;C代数系(p.327);項目56環 (pp. 153-6), 項目104群(p.281);項目229.体 (p.643).
斉藤正彦『数学の基礎：集合・数・位相』東大出版会、2002年。第2章自然数から実数体の定義まで§1代数系(pp.35-39)
本部均『新しい数学へのアプローチ5:新しい代数』共立出版、1969年、2章2.1節半群A.二項演算。
酒井文雄『共立講座21世紀の数学8：環と体の理論』共立出版、1997年、1.2節いろいろな代数系(p.3)。
志賀浩二『群論への30講』朝倉書店、1989年、第3講群の定義、pp.16-18。

神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、p. 57.
杉浦光夫『解析入門I』東京大学出版会、1980年、pp.1-2.

→[トピック一覧：順序のついた代数系]
→代数系目次・総目次