2変数関数の具体例−2変数一次関数：トピック一覧　　

　・定義：2変数一次関数/平面の方程式/法線ベクトル　
　・性質：2変数一次関数のグラフ　

　※2変数関数に関する諸概念の定義：2変数関数の定義/2変数2次関数/2変数関数の極限/連続性/偏微分/全微分/矩形上の積分/点集合上の積分/　　
　→総目次

定義：2変数1次関数

定義

・「2変数関数z=f (x,y)が1次関数である」とは、
　定数a,b,cを用いて、2変数関数z=f (x,y)を、
　　　z=f (x,y) = ax+by+c
　と表せることをいう。　

[文献]
・高橋『微分と積分2』§3.1例3.1 (p.63) ;
・小林『Mathematicaによる微積分』11.1(p.98);

※

t≠0ならば、
　「定数r,s,t,uに対し、rx+sy+t z=u が成り立つ」は、
　「zをx,yの1次関数として表せる」と同値。
　　　　なぜなら、rx+sy+t z=u を移項すると、z=−(r/t) x−(s/t) y+ u/tだから、
　　　　　　　「定数r,s,t,uに対し、rx+sy+t z=u を満たす点(x,y,z)の集合」は、
　　　　　　　　定数−(r/t), −(s/t), u/t を用いて、
　　　　　　　　zとx,yの関係を、
　　　　　　　　z=−(r/t) x−(s/t) y+ u/tと表せることを意味するから。　　　　
t=0ならば、
　「定数r,s,t,uに対し、rx+sy+t z=u が成り立つ」っても、
　「zをx,yの1次関数として表せ」ない。

類概念

1変数一次関数/ n変数一次関数　

→[トピック一覧：2変数一次関数]
→総目次

平面の方程式、法線ベクトル

設定

幾何ベクトルの空間を公理的に設定しておくべきだけども、
省略。
平面上の幾何ベクトルの説明→岡田『経済学・経営学のための数学』2.1(p.56-7)
空間上の幾何ベクトルの説明→佐武付録、斉藤付録

[文献]
・高橋『微分と積分2』§3.1例3.1 (p.63) ;
・小林『Mathematicaによる微積分』11.1(p.98);
・小形『多変数の微分積分』p.61:法線ベクトル
・『高等学校代数幾何』2章3.空間の座標とベクトルの成分(pp.52-3);5直線平面の方程式(p.63);
・斉藤『線形代数入門』1章§2-3(pp.11-3):

[yahoo]

平面

・x-y-z空間(R³)内のどの平面も、
　うまく定数r,s, t,uを調節すると、
　一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合　
　　　　{(x, y, z ) | rx+sy+t z=u }　
　として表せる。

・「平面Sの方程式はrx+sy+t z=uである」とは、
　平面Sを、　
　一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合　
　として表せるということ、
　　つまり、S = {(x, y, z ) | rx+sy+t z=u }　であること
　をいう。　

・「方程式rx+sy+t z=uが表す平面」とは、
　一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合　
　　{(x, y, z ) | rx+sy+t z=u }　
　として表せる平面のことを指す。

法線
ベクトル

・x-y-z空間(R³)内の平面S= {(x, y, z ) | rx+sy+t z=u }の法線ベクトルとは、
　　一次方程式rx+sy+t z=uにおけるx,y,zの係数を並べた
　　実3次元数ベクトル(r, s, t)　のことを言う。
・平面Sの法線ベクトルは、
　平面Sの向き(平面Sに対して垂直方向のベクトル)を意味している。

・x-y-z空間(R³)上の点(x₀,y₀,z₀)を通り、(r, s, t)を法線ベクトルとする平面は、
　一次方程式r(x- x₀)+s(y- y₀)+t (z- z₀)=０を満たす(x, y, z )をすべて集めた集合　
　　　　　　　{(x, y, z ) | r(x- x₀)+s(y- y₀)+t (z- z₀)=０}　
　として表せる。[『高等学校代数幾何』2章5 (p.63);]

例

x+y+ z=10が表す平面。
定義に戻って書き下すと、　　
　　定数r=1,s=1, t=1,u=10に対して、一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合
　　　　　　　{(x, y, z ) | rx+sy+t z=u }　
　　すなわち、x+y+ z=10を満たす(x, y, z )をすべて集めた集合　
　　　　

[Mathematicaでの左図の表示方法]

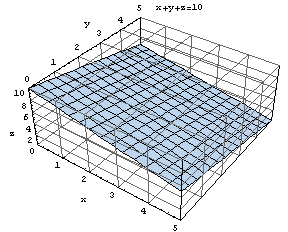
Show[Plot3D[10 - x - y, {x, 0, 5}, {y, 0, 5}], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{0, 5}, {0, 5}, {0, 10}}, ViewPoint -> {1.568, -2.186, 1.986}, AxesEdge -> {{-1, -1}, {-1, 1}, {-1, -1}}, FaceGrids -> All, PlotLabel -> "x+y+z=10"]

[z軸に平行な平面の例]

例

x=2が表す平面。
定義に戻って書き下すと、　　
　　定数r=1,s=0, t=0,u=2に対して、一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合
　　　　　　　{(x, y, z ) | rx+sy+t z=u }　
　　すなわち、x=2を満たす(x, y, z )をすべて集めた集合　


　　　

[Mathematicaでの左図の表示方法]
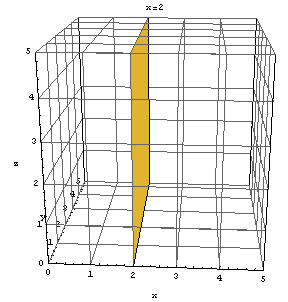
Show[Graphics3D[Cuboid[{2, -10, -10}, {2, 10, 10}]], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{0, 5}, {0, 5}, {0, 5}}, ViewPoint -> {0.190, -3.173, 1.039}, AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, FaceGrids -> All, PlotLabel -> "x=2"]

例

y =2が表す平面。
定義に戻って書き下すと、　　
　　定数r=0,s=1, t=0,u=2に対して、一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合　
　　　　　　　{(x, y, z ) | rx+sy+t z=u }　
　　すなわち、y=2を満たす(x, y, z )をすべて集めた集合
　　　

[Mathematicaでの左図の表示方法]
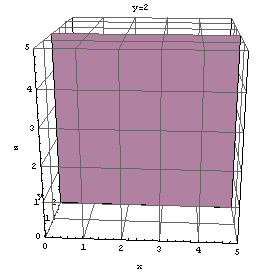
Show[Graphics3D[Cuboid[{-5, 2, -5}, {5, 2, 5}]], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{0, 5}, {0, 5}, {0, 5}}, ViewPoint -> {0.190, -3.173, 1.039}, AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, FaceGrids -> All, PlotLabel -> "y=2"]

例

x+y=1が表す平面。
定義に戻って書き下すと、　　
　　定数r=1,s=1, t=0,u=1に対して、一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合　
　　　　　　　{(x, y, z ) | rx+sy+t z=u }　
　　すなわち、x+y=1を満たす(x, y, z )をすべて集めた集合
　　　

[Mathematicaでの左図の表示方法]
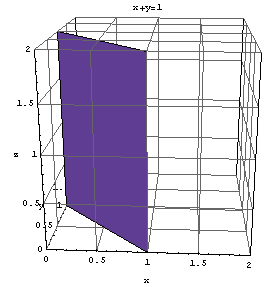
Show[Graphics3D[Polygon[{{0, 1, 0}, {1, 0, 0}, {1, 0, 5}, {0, 1, 5}}]], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{0, 2}, {0, 2}, {0, 2}}, ViewPoint -> {0.190, -3.173, 1.039}, AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, FaceGrids -> All, PlotLabel -> "x+y=1"]

例

x−y=０が表す平面。
定義に戻って書き下すと、　　
　　定数r=1,s=−1, t=0,u=0に対して、一次方程式rx+sy+t z=uを満たす(x, y, z )をすべて集めた集合　
　　　　　　　{(x, y, z ) | rx+sy+t z=u }　
　　すなわち、x−y=０を満たす(x, y, z )をすべて集めた集合
　　　

[Mathematicaでの左図の表示方法]
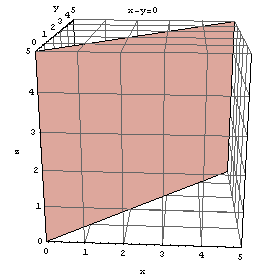
Show[Graphics3D[Polygon[{{0, 0, 0}, {5, 5, 0}, {5, 5, 5}, {0, 0, 5}}]], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{0, 5}, {0, 5}, {0, 5}}, ViewPoint -> {0.190, -3.173, 1.039}, AxesEdge -> {{-1, -1}, Automatic, {-1, -1}}, FaceGrids -> All, PlotLabel -> "x-y=0"]

→[トピック一覧：2変数一次関数]
→総目次

2変数1次関数のグラフ

グラフ

1.　2変数1次関数z=f (x,y) = ax+by+cのグラフは、
　　x-y-z空間(R³)内の平面になる。

　※なぜ？
　・グラフの定義により、
　　2変数1次関数z=f (x,y) = ax+by+cのグラフとは、
　　　z= ax+by+cを満たす(x, y, z ) を全て集めた集合 { (x, y, z ) | z=ax+by+c }
　　のこと。
　・z= ax+by+cは、ax+by−z=−cと同じだから、
　　　z= ax+by+cを満たす(x, y, z ) を全て集めた集合 { (x, y, z ) | z=ax+by+c }
　　は、
　　　ax+by−z=−cを満たす(x, y, z ) を全て集めた集合 { (x, y, z ) | ax+by−z=−c }
　　と同じ。
　・ax+by−z=−cを満たす(x, y, z ) を全て集めた集合 { (x, y, z ) | ax+by−z=−c }とは、
　　一次方程式ax+by−z=−cが表す平面、(a, b,−1)を法線ベクトルとする平面
　　に他ならない。　
　・以上から、z= ax+by+cのグラフとは、
　　(a, b,−1)を法線ベクトルとする平面であることがわかる。　　　　

2.　2変数1次関数z= a (x−x₀ )+ b (y−y₀ ) + z₀　のグラフは、
　　x-y-z空間(R³)上の点(x₀,y₀,z₀)を通り、
　　x軸方向への傾きがa、y軸方向への傾きがbの平面、　　
　　x-y-z空間(R³)上の点(x₀,y₀,z₀)を通り、(a, b,−1)を法線ベクトルとする平面となる。

[文献]
・高橋『微分と積分2』§3.1例3.1 (p.63) ;
・小林『Mathematicaによる微積分』11.1(p.98);
・小形『多変数の微分積分』p.61:法線ベクトル
・『高等学校代数幾何』2章5直線平面の方程式(p.63);
・斉藤『線形代数入門』1章§2-3(pp.11-3):

注意

2変数1次関数z=f (x,y) = ax+by+cのグラフは、どれも、x-y-z空間(R³)内の平面になる。
しかし、
x-y-z空間(R³)内のあらゆる平面を、
2変数1次関数z=f (x,y) = ax+by+cのグラフとして表せるというわけではない。

z軸に平行な平面、
詳しく言えば、
　　法線ベクトルの第三成分が0となる平面、
　　すなわち、平面の方程式rx+sy+t z=uにおけるzの係数tが0となる平面
　　　　たとえば、x=c, y=c, x+y= c, x-y= cなどが表す平面　
は、
2変数1次関数z=f (x,y) = ax+by+cのグラフとして表せない。

[例]　平面{(x, y, z ) | x =2 }＝{(x, y, z ) | 1x+０y+０z=2 }　

[例]　平面{(x, y, z ) | y =2 }＝{(x, y, z ) | ０x+1y+０z=2 }　

[例]　平面{(x, y, z ) | x+y=０}＝{(x, y, z ) | 1x+1y+０z=０ }

[例]　平面{(x, y, z ) | x−y=０}＝{(x, y, z ) | 1x−1y+０z=０ }　

なぜ、この種の平面を、2変数1次関数z=f (x,y)として表せないのか。
そもそも、2変数関数z=f (x,y)とは、「2個の実数の組(x,y)の集合からRへの写像」として定義されたが、これはすなわち、各(x,y)ごとに、対応する実数zを一個ずつ定めたものであった。
ところが、上にあげた平面では、各(x,y)に対して、実数zが一個ずつ対応していない。これらの平面では、各(x,y)に対して、無数個の実数zが対応してしまっている。
たとえば、平面{(x, y, z ) | x−y=０}においては、(x,y)が(1,1)のとき、zは０でも1でも100でもとり得るのであって、zが一個の値に決まるというようにはなっていない。
だから、各(x,y)ごとに対応する実数zを一個ずつ定める2変数関数z=f (x,y)という形式では、この種の平面を表すことはできないのである。　
　　　[杉浦『解析入門』�U§1例12(p.86)参照]

類概念

1変数一次関数のグラフ　

→[トピック一覧：2変数一次関数]
→総目次