2変数関数の具体例−2次関数：トピック一覧

　・定義：回転放物面/楕円放物面/双曲放物面/放物筒
※2変数関数に関する諸概念の定義：2変数関数の定義/2変数一次関数/2変数関数の極限/連続性/偏微分/全微分/矩形上の積分/点集合上の積分　　
→総目次

定義：回転放物面

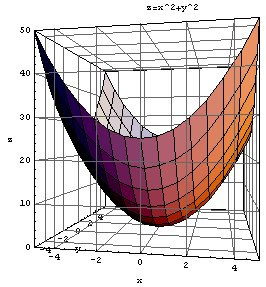
　2変数関数z=f(x,y)=x2+y2のグラフ
　　すなわち、z=f(x,y)=x2+y2を満たす(x, y, z) を全て集めた集合{ (x,y, z) | z＝x2+y2 }
　は、
　以下のようになる。
　このグラフを、回転放物面と呼ぶ。

　 回転放物面ｚ=x^2+y^2
　【文献】
  　　・高橋『微分と積分2』§3.1例3.2 (p.64)

→トピック一覧：2変数２次関数　
→総目次

定義：楕円放物面　

　2変数関数z=f(x,y)=ax2+by2 ( a＞b＞０)のグラフ
　　すなわち、z=ax2+by2を満たす(x,y,z) を全て集めた集合 { (x,y,z) | z=ax2+by2 }は、
　以下のようになる。
　このグラフを、楕円放物面と呼ぶ。

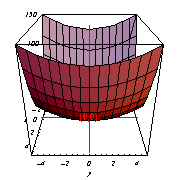
　　[例：2変数関数z=5x2+y2 のグラフ]

　 z=5x2+ y2

楕円放物面z=5x^2+y^2のグラフ


　
　【文献】
  　　・高橋『微分と積分2』§3.1例3.3 (p.65)

→トピック一覧：2変数２次関数　
→総目次

定義：双曲放物面　

・2変数関数z=f (x,y) = ax2−by2 ( a,b＞０)のグラフ
　すなわち、
　　　z= ax2−by2を満たす(x, y, z) を全て集めた集合 { (x, y, z) | z= ax2−by2 }
は、以下のようになる。
このグラフを、双曲放物面と呼ぶ。

　[z=5x2−5y2のグラフ]
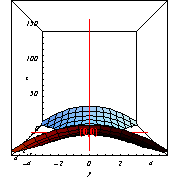
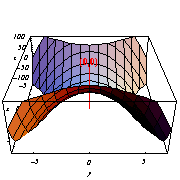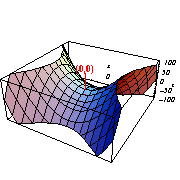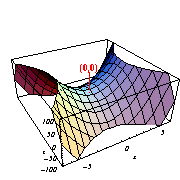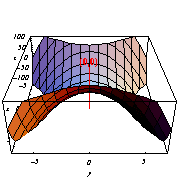
　　　　双曲放物面(z=5x^2-5y^2)のグラフ
　[z=x2- y2のグラフ]
　

双曲放物面z=x^2-y^2のグラフ




【文献】
　・高橋『微分と積分2』§3.1例3.4 (pp.65-6)
→トピック一覧：2変数２次関数　
→総目次

定義：放物筒　 　

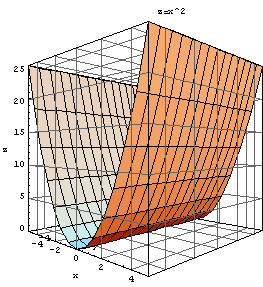
・2変数関数z=f(x,y)=ax2 ( a＞０)のグラフ
　　　すなわち、z=ax2を満たす(x, y, z) を全て集めた集合 { (x, y, z) | z=ax2}
　は、
　以下のようになる。
　 放物筒z=x^2のグラフ
　このグラフを、放物筒と呼ぶ。

【文献】
　・高橋『微分と積分2』§3.1例3.5 (pp.66-7)

→トピック一覧：2変数２次関数　
→総目次

定義：2次同次関数　、2次形式

・「2変数x,yについての二次形式」「x,yの2次同次関数」とは、
　 2変数x,yについての多項式で、2次の項ばかりからなるもの　
　　すなわち、
　　Q (x,y) = ax2+2 bxy + c y2　　　(a,b,cは定数)
　のことをいう。

※詳細→2変数2次形式　

【文献】
　・高橋『微分と積分2』§3.1定理3.6 (p.67)

定理：2次同次関数の標準形　


【文献】
　・高橋『微分と積分2』§3.1定理3.6 (p.67)

定理：2次関数の2次同次関数への帰着　

・同次でない2次関数は、平行移動すれば、同次関数に変形できる。
　でも、すべての2次関数かどうかはわからない…・

【文献】
　・高橋『微分と積分2』§3.1問5 (p.68)

→トピック一覧：2変数２次関数　
→総目次