主な関数のマクローリン展開とその証明

1.ex ＝１＋ x ＋ x2/２! ＋…＋ xn/n! ＋…　（ | x | ＜∞）
　　※なぜ？→証明　
2.log(1+ x)= x－x2/２ ＋ x3/３－…＋(－１)n－1xn/n＋…（ | x | ＜1 ）
　　※なぜ？→証明　
3.( 1+ x )a =1　＋　 ax+　＋　a(a-1)x2/2! 　＋…
　　　　　　　　　　　…＋　 a(a-1)…(a-n+1)xn/n!　＋…
　　　　　　　　　　　　　　（ | x | ＜1、a∈R）　
4.　1／(1－ x ) = 1+ x + x2  +…+ xn  +…　
5.　1／(1－ x )2 = 1 + 2 x +3 x2 +…+( n+1 ) xn +…　　
→マクローリン展開に戻る
→総目次

指数関数のマクローリン展開の証明

　　　[高木『解析概論』p.66.小平『解析入門I』 p.136,吹田新保『理工系の微分積分学』p48,高木押切『解析Ｉ・微分』p18]

【問題の定式化】

　　　　テーラーの定理：
 　　　　「f(x)を区間Iでn回微分可能な関数とする。a∈Iを定点、x∈Iを任意の点とするとき、　
　　　　　　以下の式を満たす点cがxとaの間に存在する。　
　　　　　　　　　f(x)=f(a)+f ' (a) (x－a) /(1! )＋f '' (a) (x－a)2/(2! )＋…＋f (n-1) (a) (x－a)n-1/(n-1)!＋Rn　
　　　　　　　　　　Rn= f (n) (c) (x－a)n /(n! )　　」　
　　　　ここで、f(x)=ex とすると、指数関数の微分　(ex) ' = ex 、指数関数の高次微分(dn/ dxn) ex = ex　だから、　
　　　　「　ex= ea + ea (x－a) /(1! )＋ea (x－a)2/(2! )＋…＋ea (x－a)n-1/(n-1)!＋Rn　
　　　　　　　　　　Rn= ec (x－a)n /(n! )　　
　　　　　　を満たす点cがxとaの間に存在する。」
　　　　となる。　
　　　　さらに、a=０ とすると、　　
　　　　「　ex =１＋ x ＋ x2/２! ＋…＋ xn―1/(n－1)!＋ Rn　,　
　　　　　　　　Rn= ec xn /(n! )　　　　　
　　　　　　　を満たす点cがxと０の間に存在する。すなわち０＜c＜xまたはx＜c＜０ 。　」
　　　　したがって、ex のマクローリン展開を証明するには、
　　　　　０＜ c ＜ x またはx ＜ c ＜０として、…①
　　　　　　Rn= ec xn /(n! )　
　　　　　　という数列がn→∞としたときに０に収束することを示せばよい。　

【証明】　 <

　　　| Rn |＝ | ec xn /(n! ) |= ( ec/(n! ) ) | xn |　　　∵絶対値の性質　, n>0 , e>0　
　　　　　　　　∵c<0なら直ちにc<|x| , c>0でも①より c<|x|　
　　　　　　　　
　　　　だから、　　
　　　　　　　
　　　　この最右辺→０ ( n→∞ )　　
　　　　　　　なぜなら、一般に、任意の定数aに対して、　
　　　　　　　　　　　(証明はココ！)　
　　　　　　　　これを適用して、　　
　　　　いわゆる「はさみうちの原理」より、
　　　　　　|Rn|→０ ( n→∞ )　
　　　　したがって、Rn→０ ( n→∞ )　

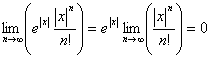
→マクローリン展開に戻る
→総目次

 log ( 1+ x )のマクローリン展開の証明　

　　　　　[吹田新保『理工系の微分積分学』p48→コーシーの剰余項を使う；高木・押切『解析Ｉ・微分』p18]　
　
【問題の定式化】


　　　　テーラーの定理：
 　　　　「f(x)を区間Iでn回微分可能な関数とする。a∈Iを定点、x∈Iを任意の点とするとき、　
　　　　　　以下の式を満たす点cがxとaの間に存在する。　
　　　　　　　　　f(x)=f(a)+f ' (a) (x－a) /(1! )＋f '' (a) (x－a)2/(2! )＋…＋f (n-1) (a) (x－a)n-1/(n-1)!＋Rn　
　　　　　　　　　　Rn= f (n) (c) (x－a)n /(n! )　　」　

　　　　ここで、f(x) = log ( 1+ x ) とすると、
　　　　　対数関数の微分 から　　{ log ( 1+ x ) }'=1/ ( 1+ x )、
　　　　　対数関数の高次微分　 (dn/ dxn) log ( 1+ x ) = (－１) n－１ (n－１) !／( 1+ x )n　　
　　　　　　　　　　　つまり、 (d2/ dx2) log ( 1+ x ) = －1／( 1+ x )2　
　　　　　　　　　　　　　　　 (d3/ dx3) log ( 1+ x ) = ＋2／( 1+ x )3　
　　　　　　　　　　　　　　　 (d4/ dx4) log ( 1+ x ) = －3!／( 1+ x ) 4　
　　　　　　　　　　　　　　　 (d5/ dx5) log ( 1+ x ) = ＋4!／( 1+ x ) 5　
　　　　　　　　　　　　　　　　　（…てな具合に、つづく…）
　　　　だから、この場合、テーラーの定理は、　
　　　　「　　
　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　
　　　　　　　　　　　　　を満たす点cがxとaの間に存在する。」　
　　　　となる。　
　　　　さらに、a=０ とすると、
　　　　「　log ( 1+ x ) = log１＋ x － x2/２! ＋２!x3/３! － ３!x４/４! ＋４!x５/５! －…
　　　　　　　　　　　　　　　　　　　　　　　…＋(－１) n―２ (n―２)！xn－１/(n－1)! ＋ Rn
　　　　　　　　　　　=x－x2/２＋x3/３－x４/４＋x５/５－…＋(－１) n―２ xn－１/(n－1) ＋ Rn　,　
　　　　　　　　　　　　
　　　　　　　を満たす点cがxと０の間に存在する。すなわち0＜ c ＜xまたはx＜ c ＜0 。　」
　　　　したがって、| x |＜1の条件下での log ( 1+ x )のマクローリン展開を証明するには、
　　　　　0＜ c ＜x または x＜ c ＜0…①
　　　　　かつ　－1＜ x ＜ 1　…②　
　　　　　として、
　　　　　　　　
　　　　　　という数列がn→∞としたときに0に収束することを示せばよい。　

【証明】　

　　　ラグランジュ剰余項　
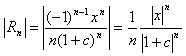　　　　　　　∵絶対値の性質、n:自然数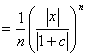　
　　　　　　　　　
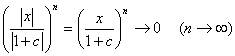
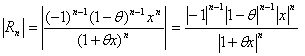　　　は、0＜x≦1ならば、収束する。
　　　　　なぜなら、　0＜ c ＜x ≦ 1なので、x ≦1＜1＋c　となって、　
　　　　　　　　　　　
　　　　　となって、|Rn|→0 ( n→∞ )。したがって、Rn→0 ( n→∞ )　
　　　ところが、－１≦x≦0のときは、これだと、微妙。　
　　　そこで、コーシーの剰余項をとる。　
　　　コーシーの剰余項は一般に、　
　　　　　　
　　　　　a=０として、　
　　　　　　　　
　　　f(x)= log ( 1+ x ) とすると、　　　　　　
　　　　対数関数の高次微分から f (n) (x)= (dn/ dxn) log ( 1+ x ) = (－１) n－１ (n－１) !／( 1+ x )n　
　　　　よって、f (n) (θx)= (dn/ dxn) log ( 1+θ x ) = (－１) n－１ (n－１) !／( 1+θx )n　
　　　なので、
　　　　　　　　
　　　　　
　　　∵絶対値の性質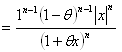　
　　　　　
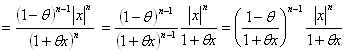
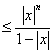　　　　　　　∵|－1|=1、　　0＜θ＜1より0＜1－θ＜1よって|1－θ|=1－θ、　
　　　　　　　　　②の－1＜xと0＜θ＜1から－1＜θxよって0＜1＋θx よって|1＋θx|＝1＋θx　
　　　　　
　　　　　∵| x |＜1(つまり－1＜x＜1)だから、(１＋xθ)は、(1－θ)と(1＋θ)の間になる。　
　　　　　　　　　　　0＜θ＜1だから、0＜(1－θ)＜(１＋xθ)＜(1＋θ)＜2　
　　　　　　　　　　　ここで0＜(1－θ)＜(１＋xθ)に注目すると、
　　　　　　　　　　　0＜(1－θ)／(１＋xθ)＜1　
　　　　　　　　　　　だから、　
　　　　　　　　　　　　　　
　　　　　∵－１＜x≦0のとき、0＜θ＜1だから、－１＜x≦θx≦0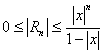　
　　　　　　　　　　　　　　　　各辺に1を足すと、0＜(1＋x) ≦(1＋θx)≦1
　　　　　　　　　　　0≦x＜１のとき、0＜θ＜1だから、－１＜－x≦0≦θx＜θ＜１
　　　　　　　　　　　　　　　　各辺に1を足すと、0＜(1－x)≦1≦(1＋θx)＜(1＋θ)＜2　
　　　　　　　　　　　つまり、－１＜x≦0で 0＜(1＋x)≦(1＋θx)、
　　　　　　　　　　　　　　　　 0≦x＜１で 0＜(1－x)≦(1＋θx)
　　　　　　　　　　　まとめると、| x |＜1で0＜( 1－| x | )≦(1＋θx)　
　　　　　　　　　　　　　　　よって、| x |＜1で　1／( 1－| x | )≧1／(1＋θx)　
　　　（ポイント）θはnが増えると変わってくるので、n→∞の極限値を求めるにあたって、どけておきたい。
　　　　　　　　　だから、こういった作業がなされている。　
　　　以上をまとめると、　
　　　　　　　
　　　この最右辺→0 ( n→∞ )　　
　　　いわゆる「はさみうちの原理」より、
　　　　　　|Rn|→0 ( n→∞ )　
　　　したがって、Rn→0 ( n→∞ )　

→マクローリン展開に戻る
→総目次
　

（reference）

『岩波数学辞典（第三版）』. 項目333　微分法[pp.983-986]
吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用　高等学校　微分・積分　新訂版』啓林館、pp.70-75;90-91;101-102.平均値定理を用いた二次の近似式まで。
矢野健太郎・田代嘉宏『社会科学者のための基礎数学　改訂版』裳華房、pp.76-77.平均値定理まで。
神谷和也・浦井憲一『経済学のための数学入門』東京大学出版会、1996年、pp.214-223(6.2.4節―6.2.6節).
高木貞治『解析概論　改訂第三版』岩波書店、1983年、pp. 47-49;61-67.
和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.54-55.pp.58-69.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.43-50.
杉浦光夫『解析入門』岩波書店、1980年、pp. 91-107. 　
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年,pp.119-126;132-138。
青本和彦『岩波講座現代数学への入門：微分と積分1』 岩波書店、1995年、pp.146-149;171-175。
高木斉・押切源一『解析Ｉ・微分』共立出版株式会社、1995年、pp.13-19。
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.55-56;61-64.
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984,pp.254-267.
Goldstein,Lay,Schneider, Calculus and Its Applications (International Editions): Eight Edition, Prentice Hall, 1999,pp.535-543;570-577.