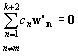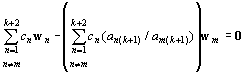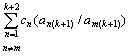一次結合が一次従属となるための十分条件（1）の証明　　
→戻る　

(舞台設定の確認)
　R：実数体(実数をすべて集めた集合）　　
　Rⁿ：実n次元数ベクトル空間　　
　+：実n次元数ベクトル空間Rⁿにおいて定義されているベクトルの加法　
　スカラーに続けてベクトルを並べて書いたもの：実n次元数ベクトル空間Rⁿにおいて定義されているスカラー乗法
　v₁, v₂, …, v_l：l個の実n次元数ベクトル。
　　　　　　　　具体的に書くと、i=1,2,…, lにたいして、v_i1, v_i2, …, v_in∈Rとして、v_i=( v_i1, v_i2, …, v_in )　　　
　　　　　　　　したがって、v₁, v₂, …, v_l ∈Ｒⁿ 。
　　　　　　　　なお、個数lが有限個であることに注意。　　
(定理の確認)
　実n次元数ベクトルv₁, v₂, …, v_lの一次結合を(l＋１)個つくる。
　これら(l＋１)個の「v₁, v₂, …, v_lの一次結合」は一次従属。
　つまり、
　　w₁＝a₁₁v₁+a₁₂v₂+…+a_1lv_l　　（a₁₁, a₁₂, …, a_1l ∈R、v₁, v₂, …, v_l ∈Ｒⁿ ）　
　　w₂＝a₂₁v₁+a₂₂v₂+…+a_2lv_l　　（a₂₁, a₂₂, …, a_2l ∈R、v₁, v₂, …, v_l ∈Ｒⁿ ）　
　　：　　
　　w_l＝a_l1v₁+a_l2v₂+…+a_llv_l　　（a_l1, a_l2, …, a_ll ∈R、v₁, v₂, …, v_l ∈Ｒⁿ ）　
　　w_(l+1)＝a_(l+1)1 v₁+a_(l+1)2v₂+…+a_(l+1)lv_l　　（a_(l+1)1, a_(l+1)2, …, a_(l+1)l ∈R、v₁, v₂, …, v_l ∈Ｒⁿ ）　
　は一次従属。　　
　　　　※「v₁, v₂, …, v_lの一次結合」も実n次元数ベクトルであることに注意。

→戻る

(証明)　[永田『理系のための線形代数の基礎』補題1.2.1(p.12);]　
任意の自然数lに対して「w₁, w₂, …, w_l, w_(l+1)は一次従属」が成り立つことを、
数学的帰納法によって示す。
つまり、
　(I) で、l=1のとき、「w₁, w₂, …, w_l, w_(l+1)は一次従属」が成り立つことを示し、
　(II) で、l=kのとき「w₁, w₂, …, w_l, w_(l+1)は一次従属」が成り立つならば、
　　　　　l=k＋1のときも、「w₁, w₂, …, w_l, w_(l+1)は一次従属」が成り立つことを示す。　

→戻る　

　
(I) l=1のとき、「w₁, w₂, …, w_l, w_(l+1)は一次従属」すなわち「w₁, w₂は一次従属」が成り立つ　　
l=1のとき、w₁＝a₁₁v₁、w₂＝a₂₁v₁　（a₁₁,a₂₁∈R、v₁∈Ｒⁿ ）　…(I-1)　
(i)「a₁₁≠０かつa₂₁≠０」であるケース　　
・実数体Rの定義により、a₁₁∈Rには、加法に関する逆元−a₁₁∈Rが存在する。　　　　
・　a₂₁w₁+(−a₁₁)w₂＝a₂₁a₁₁v₁+(−a₁₁)a₂₁v₁　　　∵(I-1)　
　　　　　　　　　＝a₁₁a₂₁v₁+(−(a₁₁a₂₁))v₁　　　∵実数の積と符号の性質　　　
　　　　　　　　　＝｛a₁₁a₂₁＋(−(a₁₁a₂₁)) ｝v₁　∵スカラーに関する分配則　
　　　　　　　　　＝０v₁　　　　　　　　　　∵実数の反数との和　　
　　　　　　　　　＝０　　　　　　　　　　　∵スカラー0倍　
上記２点より、
　w₁,w₂∈Ｒⁿに対して、スカラー−a₁₁,a₂₁∈R (−a₁₁≠０かつa₂₁≠０) が存在して、
　　　　　　　a₂₁w₁+(−a₁₁)w₂=０　　　
　を満たす。
　これは、w₁, w₂が一次従属であるということにほかならない。　
(ii)　「a₁₁≠０かつa₂₁≠０」ではないケース　　　
　　このケースでは、(I-1)より、「w₁≠０かつw₂≠０」ではない。　　　　
　　よって、定理より、w₁, w₂は一次従属。　　　　　
以上より、
l=1のとき、あらゆるケースで、　　
「w₁, w₂, …, w_l, w_(l+1)は一次従属」すなわち「w₁, w₂は一次従属」が成り立つことが示された。
→証明の先頭に戻る
(II) l=kのとき　　
　　　　「w₁, w₂, …, w_l, w_(l+1)は一次従属」すなわち「w₁, w₂, …, w_k, w_(k+1)は一次従属」が成り立つならば、
　　l=k+1でも　　
　　　　「w₁, w₂, …, w_l, w_(l+1)は一次従属」すなわち「w₁, w₂, …, w_k, w_(k+1), w_(k+2)は一次従属」が成り立つことを示す。
・仮定の分析　　
　l=kのとき、「w₁, w₂, …, w_l, w_(l+1)は一次従属」が成り立つとは、
　すなわち、「w₁, w₂, …, w_k, w_(k+1)は一次従属」が成り立つということであり、
　これは、すなわち、
　k個の「Rからつくった実n次元数ベクトル」v₁, v₂, …, v_kからつくった(k＋１)個の一次結合
　　　w₁＝a₁₁v₁+a₁₂v₂+…+a_1kv_k　　（a₁₁, a₁₂, …, a_1k ∈R、v₁, v₂, …, v_k ∈Ｒⁿ ）　
　　　w₂＝a₂₁v₁+a₂₂v₂+…+a_2kv_k　　（a₂₁, a₂₂, …, a_2k ∈R、v₁, v₂, …, v_k ∈Ｒⁿ ）　
　　　：　　
　　　w_k＝a_l1v₁+a_l2v₂+…+a_kkv_k　　（a_k1, a_k2, …, a_kk ∈R、v₁, v₂, …, v_k ∈Ｒⁿ ）　
　　　w_(k+1)＝a_(k+1)1 v₁+a_(k+1)2v₂+…+a_(k+1)kv_k　　（a_(k+1)1, a_(k+1)2, …, a_(k+1)k ∈R、v₁, v₂, …, v_k ∈Ｒⁿ ）　
　が一次従属であるということ。
・l=k+1のとき、w₁, w₂, …, w_l, w_(l+1)はw₁, w₂, …, w_k, w_(k+1), w_(k+2)であり、
　w₁, w₂, …, w_k, w_(k+1), w_(k+2)は、　　　
　(k＋１)個の「Rからつくった実n次元数ベクトル」v₁, v₂, …, v_k+1からつくった(k＋2)個の一次結合
　　　w₁＝　a₁₁v₁　+a₁₂v₂　　+…+a_1kv_k+　a_1(k+1)v_(k+1)　　（a₁₁, a₁₂, …, a_1k,a_1(k+1)∈R、v₁, v₂, …, v_k, v_k+1 ∈Ｒⁿ ）　
　　　w₂＝　a₂₁v₁　+a₂₂v₂　　+…+a_2kv_k　+a_2(k+1)v_(k+1)　　　（a₂₁, a₂₂, …, a_2k,a_2(k+1)∈R、v₁, v₂, …, v_k, v_k+1 ∈Ｒⁿ ）　
　　　：　　
　　　w_k＝　a_k1v₁　+a_k2v₂　　+…+a_kkv_k　+a_k(k+1)v_(k+1)　　　（a_k1, a_k2, …, a_kk,a_k(k+1)∈R、v₁, v₂, …, v_k, v_k+1 ∈Ｒⁿ ）　
　　　w_(k+1)＝a_(k+1)1 v₁+a_(k+1)2v₂+…+a_(k+1)kv_k+a_(k+1)(k+1)v_(k+1)　（a_(k+1)1,a_(k+1)2,…, a_(k+1)k,a_(k+1)(k+1)∈R、v₁, v₂, …, v_k , v_k+1∈Ｒⁿ ）　
　　　w_(k+2)＝a_(k+2)1 v₁+a_(k+2)2v₂+…+a_(k+2)kv_k+a_(k+2)(k+1)v_(k+1)　（a_(k+2)1,a_(k+2)2,…, a_(k+2)k,a_(k+2)(k+1)∈R、v₁, v₂, …, v_k , v_k+1∈Ｒⁿ ）　
　である。
・v_(k+1)の係数a_1(k+1) ,a_2(k+1) , … , a_k(k+1) ,a_(k+1)(k+1) , a_(k+2)(k+1) がすべてゼロである場合と、そうでない場合に分けて、　
　　w₁, w₂, …, w_k, w_(k+1), w_(k+2)が一次従属であることを示す。　　　
・v_(k+1)の係数a_1(k+1) ,a_2(k+1) , … , a_k(k+1) ,a_(k+1)(k+1) , a_(k+2)(k+1) がすべてゼロである場合、
　　スカラー0倍と零ベクトルの加法則より、　　　　　
　　　w₁＝a₁₁v₁+a₁₂v₂+…+a_1kv_k　　（a₁₁, a₁₂, …, a_1k ∈R、v₁, v₂, …, v_k, v_k+1 ∈Ｒⁿ ）　
　　　w₂＝a₂₁v₁+a₂₂v₂+…+a_2kv_k　　　（a₂₁, a₂₂, …, a_2k ∈R、v₁, v₂, …, v_k, v_k+1 ∈Ｒⁿ ）　
　　　：　　
　　　w_k＝a_k1v₁+a_k2v₂+…+a_kkv_k　　　（a_k1, a_k2, …, a_kk ∈R、v₁, v₂, …, v_k, v_k+1 ∈Ｒⁿ ）　
　　　w_(k+1)＝a_(k+1)1 v₁+a_(k+1)2v₂+…+a_(k+1)kv_k　（a_(k+1)1, a_(k+1)2, …, a_(k+1)k ∈R、v₁, v₂, …, v_k , v_k+1∈Ｒⁿ ）　
　　　w_(k+2)＝a_(k+2)1 v₁+a_(k+2)2v₂+…+a_(k+2)kv_k　（a_(k+2)1, a_(k+2)2, …, a_(k+2)k ∈R、v₁, v₂, …, v_k , v_k+1∈Ｒⁿ ）　
　である。
　すると、w₁, w₂, …, w_k, w_(k+1)は仮定と同じモノであるから、これらは仮定より、一次従属。
　ならば、一次従属なベクトルの集合に、ベクトルを加えても一次従属だから、∵　
　仮定のもとで、w₁, w₂, …, w_k, w_(k+1), w_(k+2)は一次従属である。

・「v_(k+1)の係数a_1(k+1) ,a_2(k+1) , … , a_k(k+1) ,a_(k+1)(k+1) , a_(k+2)(k+1) のすべてがゼロ」というわけではない場合　
　v_(k+1)の係数a_1(k+1) ,a_2(k+1) , … , a_k(k+1) ,a_(k+1)(k+1) , a_(k+2)(k+1) の少なくとも一つは、ゼロではない場合。
　v_(k+1)の係数a_1(k+1) ,a_2(k+1) , … , a_k(k+1) ,a_(k+1)(k+1) , a_(k+2)(k+1) のなかの、ゼロではない少なくとも一つを、
　a_m(k+1)　(ただし、 mは自然数で、1≦m≦k+2 を満たす)　とおき、
　v₁, v₂, …, v_(k+1)からつくった(k＋2)個の一次結合のうち、
　v_(k+1)の係数がa_m(k+1)≠0である、v₁, v₂, …, v_k+1の一次結合を、　　
　　w_m＝a_m1v₁+a_m2v₂+…+a_mkv_k+a_m(k+1)v_(k+1)　（a_m1, a_m2, …, a_mk,a_m(k+1)∈R、v₁, v₂, …, v_k, v_k+1∈Ｒⁿ ,1≦m≦k+2）
　とおく。
　v₁, v₂, …, v_k+1からつくった(k＋2)個の一次結合のうち、
　　w_m以外の一次結合w_n( nは自然数で、1≦n≦k+2かつn≠m)から、　　
　　　　w_n'=w_n−(a_n(k+1)/a_m(k+1))w_m　　
　　　　　　=w_n−(a_n(k+1)/a_m(k+1))（a_m1v₁+a_m2v₂+…+a_mkv_k+a_m(k+1)v_(k+1)　）
　　　　　　=w_n−（(a_m1a_n(k+1)/a_m(k+1))v₁+(a_m2a_n(k+1)/a_m(k+1))v₂+…+(a_mka_n(k+1)/a_m(k+1))v_k+a_n(k+1)v_(k+1)　）　　
　　　　　　= a_n1v₁+a_n2v₂+…+a_nkv_k+a_n(k+1)v_(k+1)
　　　　　　　　−（(a_m1a_n(k+1)/a_m(k+1))v₁+(a_m2a_n(k+1)/a_m(k+1))v₂+…+(a_mka_n(k+1)/a_m(k+1))v_k+a_n(k+1)v_(k+1)　）　　
　　　　　　= (a_n1−a_m1a_n(k+1)/a_m(k+1))v₁+(a_n2−a_m2a_n(k+1)/a_m(k+1))v₂+…+(a_nk−a_mka_n(k+1)/a_m(k+1))v_k　
　　をつくる。
すると、
　w_n'=(a_n1−a_m1a_n(k+1)/a_m(k+1))v₁+(a_n2−a_m2a_n(k+1)/a_m(k+1))v₂+…+(a_nk−a_mka_n(k+1)/a_m(k+1))v_k　
　　　　　　　　　( nは自然数で、1≦n≦k+2かつn≠m)　　
　は、(a_n1−a_m1a_n(k+1)/a_m(k+1)), (a_n2−a_m2a_n(k+1)/a_m(k+1)),…,(a_nk−a_mka_n(k+1)/a_m(k+1))∈Rだから、
　v₁, v₂, …, v_k の一次結合。　　　　
ならば、w'₁, w'₂, … , w'_k , w'_(k+1) , w'_(k+2)　から、w'_mを除いた、(k＋１)個のv₁, v₂, …, v_k の一次結合は、　
仮定より、一次従属である。　
一次従属の定義により、
　n＝mを除く、n=1,2,…, k, k+1, k+2　について、 全部は0ではないc_nが存在して、　
　　　　
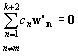
　を満たす。　
ここで、w_n'= w_n−(a_n(k+1)/a_m(k+1))w_m　を代入。
　　c_nw_n'=c_nw_n−c_n(a_n(k+1)/a_m(k+1))w_m　だから、
　　　　
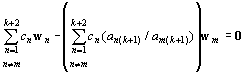
w_mの係数
　　　
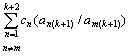
は実数体Rに属し、　　　　
また、n＝mを除く、n=1,2,…, k, k+1, k+2　にたいするc_nは少なくとも一つゼロでないものを含むから、　
これは、　
w₁, w₂, …, w_k, w_(k+1), w_(k+2)は一次従属であることを示している。　　

※mがたまたま2<m<kであったときの具体例　
｜w'₁＝w₁−(a_1(k+1)/a_m(k+1))w_m＝(a₁₁−a_m1a_1(k+1)/a_m(k+1))v₁+(a₁₂−a_m2a_1(k+1)/a_m(k+1))v₂+…+a_1kv_k　　　　　　
｜w'₂＝w₂−(a_2(k+1)/a_m(k+1))w_m＝(a₂₁−a_m1a_2(k+1)/a_m(k+1))v₁+(a₂₂−a_m2a_2(k+1)/a_m(k+1))v₂+…+(a_2k−a_mka_2(k+1)/a_m(k+1))v_k　
｜：　
｜w'_m−1＝w'_m−1−(a_(m−1)(k+1)/a_m(k+1))w_m　
｜　　　= (a_(m−1)1−a_m1a_(m−1)(k+1)/a_m(k+1))v₁+(a_(m−1)2−a_m2a_(m−1)(k+1)/a_m(k+1))v₂+…+(a_(m−1)k−a_mka_(m−1)(k+1)/a_m(k+1))v_k　　
｜w'_m＋1＝w'_m＋1−(a_(m＋1)(k+1)/a_m(k+1))w_m　
｜　　　= (a_(m＋1)1−a_m1a_(m＋1)(k+1)/a_m(k+1))v₁+(a_(m＋1)2−a_m2a_(m＋1)(k+1)/a_m(k+1))v₂+…+(a_(m＋1)k−a_mka_(m＋1)(k+1)/a_m(k+1))v_k　　
｜：　
｜w'_k＝w_k−(a_k(k+1)/a_m(k+1))w_m= (a_k1−a_m1a_k(k+1)/a_m(k+1))v₁+(a_k2−a_m2a_k(k+1)/a_m(k+1))v₂+…+(a_kk−a_mka_k(k+1)/a_m(k+1))v_k　
｜w'_(k+1)＝w_(k+1)−(a_(k+1)(k+1)/a_m(k+1))w_m　　　　
｜　　　= (a_(k+1)1−a_m1a_(k+1)(k+1)/a_m(k+1))v₁+(a_(k+1)2−a_m2a_(k+1)(k+1)/a_m(k+1))v₂+…+(a_(k+1)k−a_mka_(k+1)(k+1)/a_m(k+1))v_k　　　
｜w'_(k+2)＝w_(k+2)−(a_(k+2)(k+1)/a_m(k+1))w_m　　　　　　
｜　　　= (a_(k+2)1−a_m1a_(k+2)(k+1)/a_m(k+1))v₁+(a_(k+2)2−a_m2a_(k+2)(k+1)/a_m(k+1))v₂+…+(a_(k+2)k−a_mka_(k+2)(k+1)/a_m(k+1))v_k　

→戻る