|
戻る→[基本行列] 戻る→[行基本変形] [列基本変形] |


|
戻る→[基本行列] 戻る→[行基本変形] [列基本変形] |
(本題1)



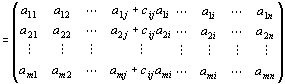 ∵行列積の定義
∵行列積の定義 

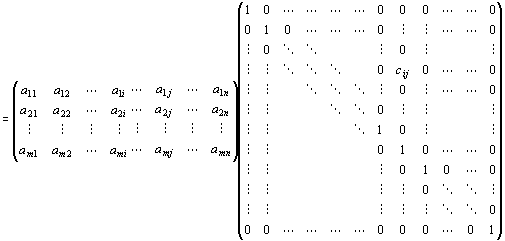
 ∵行列積の定義
∵行列積の定義
|
戻る→[基本行列] 戻る→[行基本変形] [列基本変形] |

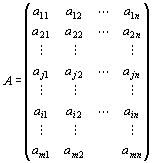

 ∵行列積の定義
∵行列積の定義 


 ∵行列積の定義
∵行列積の定義
|
戻る→[基本行列] 戻る→[行基本変形] [列基本変形] |

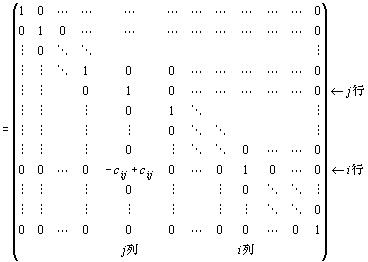 ∵行列積の定義
∵行列積の定義 
 ∵行列積の定義
∵行列積の定義 
 ∵行列積の定義
∵行列積の定義 
 ∵行列積の定義
∵行列積の定義 |
戻る→[基本行列] 戻る→[行基本変形] [列基本変形] |