分布関数（
1次元）仮定：
確率空間
確率変数 X: Ω→R1
PX: Xの確率分布 on
つまり、
Px ( (a, b] )≡P( {ω∈Ω| a＜X(ω)≦b } )= P ( {ω∈Ω|X (ω) ∈ (a, b] } )
= P ( X-1 ( (a, b] ) )
とする。
(Distribution Function)cf. 二次元の同時(結合)分布関数、多次元の同時分布関数(結合分布関数)の定義
FX(x)=PX ( (-∞,x] )= P ( {ω∈Ω| X(ω)≦x } ), x∈R1
なる
FX : R1→[0,1]
を、
X (もしくはPX) の分布関数という。
※ 略記法
{ω∈Ω| a＜X(ω)≦b}は{ a＜X≦b }
{ω∈Ω| X (ω)∈B}は{ X∈B }
などと略記される。
野田・宮岡『数理統計学の基礎』p15. 1：
P ( {ω∈Ω| a＜X(ω)≦b } )=Fx(b)−Fx (a)
（証明）
Fx (b) = P ( {ω∈Ω|X(ω)≦b} ) ∵分布関数の定義
= P ( {ω∈Ω|X(ω)≦a } ∪ {ω∈Ω| a ＜X(ω)≦ b } )
= P ( {ω∈Ω|X(ω)≦a } )＋ P ({ω∈Ω| a ＜X(ω)≦ b } ) ∵確率の有限加法性
= Fx (a)＋ P ({ω∈Ω| a ＜X(ω)≦ b } ) ∵分布関数の定義
移項して、
P ({ω∈Ω| a ＜X(ω)≦ b } )= Fx (b)−Fx (a)
2： 分布関数の性質
cf. 二次元の同時(結合)分布関数の性質、多次元の同時(結合)分布関数の性質
分布関数Fx (・)は次の性質をもつ。
(1) 0≦Fx(x)≦1, for ∀x∈R1
(2) x ＜y ⇒Fx(x)≦Fx(y)
すなわち、
Fx(x)は単調非減少関数。(3-1)
(3-2)
(4) Fx (x)は右連続関数である。
すなわち、
for ∀ x ∈ R1
(証明)
(1) Fxは確率変数Xの確率分布 PXとして定義されている。
確率分布もまた確率の公理を満たす確率であるので（∵定理）、。
0≦Fx(x)≦1
(2) x＜yを任意にとる。
x＜yより、{X≦x }⊂{X≦y }
ゆえに、
{ω∈Ω| X(ω)≦x }⊂{ω∈Ω| X(ω)≦y }よって、
確率の単調性から、P({ω∈Ω| X(ω)≦x }) ≦ P({ω∈Ω| X(ω)≦y })
確率分布の定義を用いて言い換えれば、すなわち、
P X ( (-∞, x ] ) ≦ P X ( (-∞, y ] )
分布関数の定義を用いて言い換えれば、すなわち、
Fx(x)≦Fx(y)
(3-1)
の証明
∵
解析学における「関数の収束」と「数列の収束」を関連づけた定理：「
x →x0 のとき、f(x)がAに収束する」ならば、「
x0 に収束するどんな数列 { xn }（ただし、xn ≠x0 ）に対しても、数列
{ f ( xn ) }がAに収束する」また、逆も成り立つ。
ボクのみたところ、同様に、
「
x →∞のとき、f(x)がAに収束する」ならば、「∞に発散するどんな数列{
xn }に対しても、数列 { f ( xn ) }がAに収束する」逆も成り立つ、
ともいえる。
なぜかは、こちら。＊
実数での極限を自然数での極限(可算無限)に置き換え。集合列の極限に帰着させるため。鈴木山田『数理統計学）』p25では(2)で正当化しているが、なぜそうできるのか？？
∵分布関数の定義
∵確率分布の定義
ここで、上式で極限を考えた集合{
ω∈Ω｜X(ω)≦n}をAnとおく。集合列{
An}の極限に関する性質について、考えてみよう。集合列{
An}は、An⊂ An+1 となるので、増大列。したがって、集合列{
An}には極限が存在し、
={ω∈Ω｜X(ω)＜∞}=Ω (＊)
また、
増大列であることから、確率の連続性が成り立ち。
(＊＊)
以下本題にもどって、
∵(＊＊)
=P(Ω) ∵(＊)
=1 (確率の公理P2)
→
鈴木山田『数理統計学）』p25。柳川堯『統計数学』p15。(3-2)
の証明
∵
解析学における「関数の収束」と「数列の収束」を関連づけた定理：「
x →x0 のとき、f(x)がAに収束する」ならば、「
x0 に収束するどんな数列 { xn }（ただし、xn ≠x0 ）に対しても、数列
{ f ( xn ) }がAに収束する」。また、逆も成立する。
＊実数での極限を自然数での極限
(可算無限)に置き換え。集合列の極限に帰着させるため。鈴木山田『数理統計学）』p25では(2)で正当化しているが、なぜそうできるのか？？
∵分布関数の定義
∵確率分布の定義
ここで、上式で極限を考えた集合{
ω∈Ω｜X(ω)≦−n}をAnとおく。集合列{
An}の極限に関する性質について、考えてみよう。集合列{
An}は、An⊃An+1 となるので、減少列。したがって、集合列{
An}には極限が存在し、
＝{
ω∈Ω｜−∞＜X(ω)≦−1}∩{ω∈Ω｜−∞＜X(ω)≦−2}∩……
∩{ω∈Ω｜−∞＜X(ω)≦−100}∩……
∩{ω∈Ω｜−∞＜X(ω)＜−∞}＝
φ (＊)また、
減少列であることから、確率の連続性が成り立ち。
(＊＊)
以下本題にもどって、
＝Ｐ（
φ ） (＊)＝
0 ∵定理：空事象の確率→
鈴木山田『数理統計学）』p25。(4)「Fx (x)は右連続関数である」の証明
※関連重要事項→
右極限、右連続x∈Rを任意にとる。
∵・
解析学における「関数の収束」と「数列の収束」を関連づけた定理：「
x →x0 のとき、f(x)がAに収束する」ならば、「
x0 に収束するどんな数列 { xn }（ただし、xn ≠x0 ）に対しても、数列
{ f ( xn ) }がAに収束する」。また、逆も成立する。
これを、片側
(x >x0)に制限して、証明しなおせばよい。・
Fxが単調非減少関数。
∵分布関数の定義
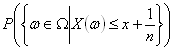∵確率分布の定義
ここで、上式で極限を考えた集合{
ω∈Ω｜X(ω)≦x+1/n } をAnとおく。集合列{
An}の極限に関する性質について、考えてみよう。集合列{
An}は、An⊃An+1 となるので、減少列。したがって、集合列{
An}には極限が存在し、
＝{
ω∈Ω｜−∞＜X(ω)≦x+1}∩{ω∈Ω｜−∞＜X(ω)≦x +1/2}∩……
∩{ω∈Ω｜−∞＜X(ω)≦ x +1/100 }∩……
∩{ω∈Ω｜−∞＜X(ω)≦x }＝
{ω∈Ω｜−∞＜X(ω) ≦x } (＊)また、
減少列であることから、確率の連続性が成り立ち。
(＊＊)
以下本題にもどって、
∵
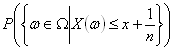
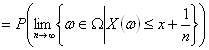＝Ｐ（
{ω∈Ω｜−∞＜X(ω) ≦x } ） ∵ （＊）=P X ( (−∞,x] ) ＝FX(x) ∵ 分布関数の定義
3：
上の確率分布と、確率分布関数は、一対一に対応する。
つまり、
確率分布
PX が与えられるとその分布関数Fx(x)が定義され、逆に、
分布関数
Fx(x)が与えられると、それを分布関数として持つ唯一つの確率分布
PX が存在する。(証明)
略
4：
ある
F:R1→R1が定理
2(1)-(4)を満たすなら、 上の確率
P( (−∞,x] )=F(x) for ∀x∈R1
(証明)
略
（
reference）文献
1.『岩波数学辞典（第三版）』項目47C(p.128).文献
2. 佐藤坦『はじめての確率論 測度から確率へ』共立出版、1994、pp.27-28.文献
3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、pp.24-26。文献
4. 柳川堯『統計数学』近代科学社、1990年,pp.14-15.文献
5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、pp.17-18 。