定義：Px,　Px　

　確率空間　、

　X:Ω→R 1とする確率変数、

　　ないし、

　X:Ω→R nとする確率ベクトル、X=(X1,X2,…,Xn)

　とする。

（ボレル集合の概念を用いない特殊的な定義）

　Px ( (a,b] )を以下のように定義する。

　Px ( (a, b] )≡P( {ω∈Ω| a＜X(ω)≦b } )= P ( {ω∈Ω|X (ω) ∈ (a, b] } )

　　　　　　　　　　 = P (　X-1 (　(a, b]　)　)

　　　　　　　　　

　※　略記法

　　　{ω∈Ω| a＜X(ω)≦b}は{ a＜X≦b }

　　　{ω∈Ω| X (ω)∈B}は{ X∈B }

　　　などと略記される。

　　　　　　　野田・宮岡『数理統計学の基礎』p15.

　

（ボレル集合の概念を用いた一般的な定義）

　∀B∈　に対して、Px ( B )≡P (　X-1 (B)　)

　∀B∈　に対して、Px ( B )≡P (　X-1 (B)　)

　　　

定理

　確率空間　、X:Ω→R1とする確率変数とすると、

　　∀B∈に対して、Px ( B )≡P (　X-1 (B)　)は(R1, )上の確率。(R1, , Px) は確率空間。

　　∀B∈に対して、Px ( B )≡P (　X-1 (B)　)は(R1, )上の確率。(R1, , Px) は確率空間。

　　　（証明）

　　　Pxが(R1, )において、確率の公理、すなわち、

　　　　　(P1)　0≦ Px (B)≦1　∀B∈

　　　　　(P2)　Px (R1)=1

　　　　　(P3)　B1,B2,…∈, Bi∩Bj=φ (i≠j) ⇒

　　　　　　　　　　　　　　　　　　　　　(完全加法性/可算加法性)

　　　を満たすことを示せばよい。

　　　(P1を満たすことの証明)

　　　　0≦Px ( B )≡P (　X-1 (B)　) ≦1　

　　　　　　∵Pは上の確率として定義されているので、以下の性質を満たす。

　　　　　　　　　　　　　　　　(P1)　0≦P (A)≦1　,∀A∈A,

　　　(P2を満たすことの証明)

　　　　Px (R1)= P (　X-1 (　(-∞, ∞)　)　)=P(Ω)=1

　　　　　　∵Pは上の確率として定義されているので、以下の性質を満たす。

　　　　　　　　　　　　　　　　(P2)　P(Ω)=1

　　　(P3を満たすことの証明)

　　　　B1,B2,…∈, Bi∩Bj=φ (i≠j)とする。

　　　　　

　　　　　　　　　　　　　　　　　　　　　∵PXの定義

　　　　　　　　　　　　　∵　unionの逆像　

　　　　　　　　　　　　　∵　上の確率Pは(P3)完全加法性を満たす。

　　　　　　　　　　　　　

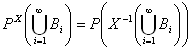
　　　　　　　　　　　　　　　　　　　　　∵PXの定義

　　　　　（野田・宮岡『数理統計学の基礎』p.16.の省略部を自力で埋めたもの）

定義：Xの確率分布

　・Pxを確率変数Xの確率分布という。

　　　　　　Px ( (a, b] )≡P( {ω∈Ω| a＜X(ω)≦b } )= P ( {ω∈Ω|X (ω) ∈ (a, b] } )

　　　　　　　　　　 = P (　X-1 (　(a, b]　)　)

　・Pxをn次元確率ベクトルXの確率分布という。

　　　　　　Px( (a1, b1]×(a2, b2]×…×(an, bn] ) ≡ P(X1,X2….,Xn) ( (a1, b1]×(a2, b2]×…×(an, bn] )　

　　　　　　≡P( {ω∈Ω| a1＜X1(ω)≦b1,…, an＜Xn(ω)≦bn } )

　　　　　　= P ( {ω∈Ω|　X1 (ω) ∈ (a1, b1],…, Xn (ω) ∈ (an, bn] } )

　　　　　　= P ( {ω∈Ω|　X1 (ω) ∈ (a1, b1],…, Xn (ω) ∈ (an, bn] } )

　　　　　　= P ( {ω∈Ω|　X (ω) ∈ (a1, b1]×(a2, b2]×…×(an, bn] } )

　　　　　　= P (　X-1 (　(a1, b1]×(a2, b2]×…×(an, bn]　)　)

　＊Pxを確率と呼んでよいかについては、こちら。　　

定義：同時分布(simultaneous distribution)、結合分布(joint distribution)

　　　n次元確率ベクトルX=(X1,X2,…,Xn)の確率分布 Px=P(X1,X2….,Xn)　　

　　　　　　　　　　　　　　を同時分布という。

　　Px( (a1, b1]×(a2, b2]×…×(an, bn] ) ≡ P(X1,X2….,Xn) ( (a1, b1]×(a2, b2]×…×(an, bn] )　

　　　　　≡P( {ω∈Ω| a1＜X1(ω)≦b1,…, an＜Xn(ω)≦bn } )

　　　　　= P ( {ω∈Ω|　X1 (ω) ∈ (a1, b1],…, Xn (ω) ∈ (an, bn] } )

　　　　　= P ( {ω∈Ω|　X1 (ω) ∈ (a1, b1],…, Xn (ω) ∈ (an, bn] } )

　　　　　= P ( {ω∈Ω|　X (ω) ∈ (a1, b1]×(a2, b2]×…×(an, bn] } )

　　　　　= P (　X-1 (　(a1, b1]×(a2, b2]×…×(an, bn]　)　)

　

定義：周辺分布(marginal distribution)

　　　n次元確率ベクトルX=(X1,X2,…,Xn)とする。

　　・X1の周辺分布とは、

　　　　∀B∈に対し、

　　　　PX1 (B)= P( X1−1(B) )=P(　{ω∈Ω|X1 (ω)∈B,　X2(ω)∈R1,　…　, Xn(ω)∈R1}　)

　　　　　　　 =　P(　{ω∈Ω|X∈B1×R1×…×R1}　)

　　　　　　　 =　Px (B1×R1×…×R1)

　　・Xiの周辺分布とは、

　　・の周辺分布『数理統計学―基礎から学ぶデータ解析―（第二版）』p.22.

　　　　

　

定理：確率変数の関数の確率分布

　Xを上の確率変数とする。

　h : R → R がBorel可測関数であれば、

　Y= h (X)は確率変数となるが、

　その確率分布P Yは

　P Y ( B )=P X [ h−1 ( B ) ], B∈

　

　　（証明）

　　　写像Y:　Ω∋ω→h [X(ω)]∈Rを考える。

　　　各B∈に対し、　Y−1 (B) = X−1 [ h−1 (B) ]

　　　P Y ( B ) = P ( Y−1 (B) ) 　　　　　　　　∵確率分布の定義

　　　　　　　= P [ X−1 { h−1 (B) } ]　　　　∵　（※）より

　　　　　　　= P X [ h−1 ( B ) ]　　　　　　　∵　確率分布の定義

　　　　　　　（野田・宮岡『数理統計学の基礎』Pp.24-25。)

　　　（別の表現？）

　　　P Y ( B ) = P ( {ω∈Ω|Y(ω)∈B} )　　　∵確率分布の定義

　　　　　　　= P ( {ω∈Ω|h( X(ω) )∈B} )　　　∵仮定よりY= h (X)

　　　　　　　= P ( {ω∈Ω|X(ω)∈h-1(B) } )　　　

　　　　　　　＝P X ( h−1 (B) )　　∵h : Borel可測関数よりh-1(B) ∈

　　　　　　　　　　　　　　　　　ゆえに、先の式は

　　　　　　　　　　　　　　　　　Xの確率分布の定義に合致する。

　

（reference）

文献1.『岩波数学辞典（第三版）』項目47C(p.128).

文献2. 佐藤坦『はじめての確率論　測度から確率へ』共立出版、1994、pp.89-99.

文献3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、pp.21-22。

文献4. 矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p.150-155.　

文献5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.16、pp.27-32 。