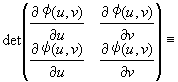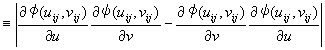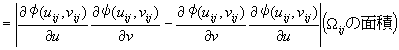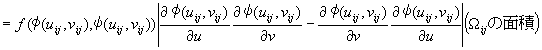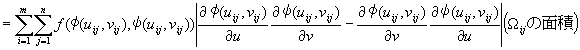2�d�ϕ��ɂ�����ϐ��ϊ������@
�@
�����ڎ��ɖ߂�B�@
�ϐ��ϊ��ɂ��ʐς̕ω�
[���w��͊T�_�x8��96��(pp.351-355); ���c�V�ہw���H�n�̔����ϕ��w�x205;���`�w���ϐ��̔����ϕ��x99-101;
�@���Y�w��͓���II�xVII�́�4(pp.106-110.);�}���w�����ϕ��w�x7.3�� (pp.266-270)�B]
�i����ݒ�j
���Fu-v���ʏ���̈��@
P(uo,vo):�@�����̈�_�B
A�F�@P���܂ރ���̖ʐϊm��ȋ��
��:�@A�̌a�B
D�Fx-y���ʏ���̈��@
x=��(u,v) ,y=��(u,v) :����D��Ɏʂ���Έ�Ή��B��, �Ղ́AC1�����B
P'(��(uo,vo) ,��(uo,vo)): ��(u,v) ,��(u,v)�ɂ���āAP(uo,vo)��x-y���ʏ��D��Ɏʂ������B
A': ��(u,v) ,��(u,v)�ɂ���āA����x-y���ʏ��D��Ɏʂ������B�ʐϊm��ɂȂ�B�@�@
�i�{��j
�ρ�0�Ƃ��āAA��_P(uo,vo)�Ɏ���������ƁA
����ɑΉ����āAA'���_P'(��(uo,vo) ,��(uo,vo))�Ɏ�������B
���̂Ƃ��AA��A'�̖ʐϔ�́A�_P(uo,vo)�ɂ��������R�r�A���̐�Βl�ɓ������Ȃ�B
�܂�A
�@�@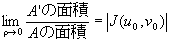
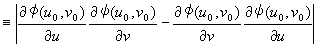
2�d�ϕ��ɂ�����ϐ��ϊ�����
[���Y�w��͓���II�xVII�́�4(pp.110-119.); ���c�V�ہw���H�n�̔����ϕ��w�x205;
�@���w��͊T�_�x8��96��(pp.355-359);���c�w�����ϕ��x10��3��(365-73.);
�@�}���w�����ϕ��w�x7.3�� (pp.266-270); ���`�w���ϐ��̔����ϕ��x95-106.]
�i����ݒ�j
���Fu-v���ʏ���̈��@
D�Fx-y���ʏ���̈��@
x=��(u,v) ,y=��(u,v):����D��Ɏʂ���Έ�Ή��B
�i�{��j
����P�F��(u,v) ,��(u,v)�������C1�����@
����Q�F���R�r�A��������[���ɂȂ�Ȃ��A���Ȃ킿�A�C�ӂ�(u,v)�����ɑ��āA
�@�@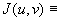
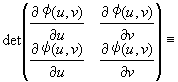
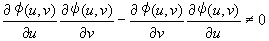
����3�F��f(x,y)��D���ϕ��@
�����藧���Ȃ���A
���_1: �@ f(��(u,v) ,��(u,v))�������ϕ��@
�ƂȂ��āA�@
���_2:�@D��̊�f���ϕ����A����̍�����f (��(u,v) ,��(u,v)) J(u,v) ���ϕ��ŕ\���āA
�@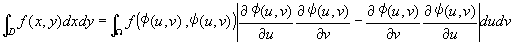
�i���������̒����I�Ȑ����j
[���c�V�ہw���H�n�̔����ϕ��w�x205; ���`�w���ϐ��̔����ϕ��x95-106;���w��͊T�_�x8��96��(pp.355-356);]
step1:
�܂��A���������d�ϕ��Ƃ͉��������̂���U��Ԃ��Ă����B
�Ƃ肠�����AD����`�Ƃ��Ęb��i�߂�
(��ʂ̗L�E�W����̐ϕ����A���ǂ́A��`��̐ϕ��ɋA�����ꂽ)�B
�@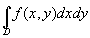 �Ƃ́A
�Ƃ́A
�@D��������������Ȃ��ׂ������Ă������Ƃ��́Af(x ,y )�����[�}���a�̋Ɍ��ł������B
�@���[�}���a�Ƃ͂��������A
�@�@D���������ɂ���Ăł�������` Dij�̖ʐςƁADij��̓_(xij, yij)�ɂ�������f (xij , yij)�̒l�̐ς��A
�@�@���ׂĂ�����`�ɂ��đ����������a�ł������B
�@������A�@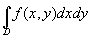 �Ƃ́A
�Ƃ́A
�@�@�@�@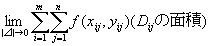
�@�ɂق��Ȃ�Ȃ��B
Step2:
�����ŁAx=��(u,v) ,y=��(u,v)��p���āA��̐ϕ��̒�`���Ax,y�̎�����Au,v�̎��ŕ\���Ă݂邱�Ƃɂ���B
1. �܂��Af (xij , yij)�́Ax=��(u,v) ,y=��(u,v)�����̂܂ܑ�����āAf (��(uij , vij) ,��(uij , vij ) )�ŕ\���Ηǂ��B
�@���̕ϐ��ϊ��́Ax,y���Au,v��p�������ŕ\���悤�ɏ��������邾��������A��f(x,y)���͕̂ς��Ȃ��B
2. ���ɁAx-y ���Dij�̖ʐςł��邪�A�����u-v��ɂ�������ij�Ƃ́A���������ʐς��������Ă���B
�@�����ł́A������������Ȃ��ׂ������Ă������Ƃ����l���Ă���̂ŁA�藝���Ȃ肽���A
�@�@
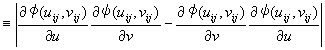
�@�܂�A|��|��0�ŁA
�@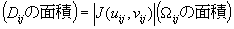
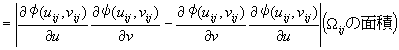
�@�ƂȂ�B
3. ����āA|��|��0�ŁA
�@�@f (xij , yij)(Dij�̖ʐ�)=�@
�@�@�@�@�@�@�@�@�@�@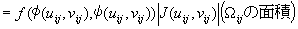
�@�@�@�@�@�@�@�@�@�@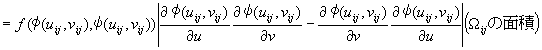
�@��̓�����S�Ă�����`�ɂ��đ����������a���Ƃ�ƁA
�@|��|��0�ŁA
�@�@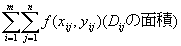
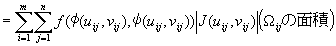
�@�@�@�@�@�@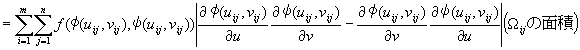
Step3:
|��|��0�Ƃ����ۂ̏㎮�̍��ӂ́A
�@�@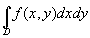
�@�̒�`�A
|��|��0�Ƃ����ۂ̉E�ӂ́A
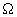 ��
��
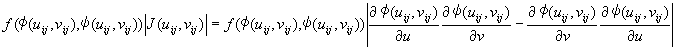
�̃��ɂ�������ʃ��[�}���a��|��|��0�Ƃ����ۂ̋Ɍ��ƂȂ邪�A
���ꂪ��������A�藝���A
�@�@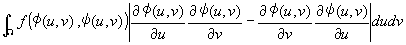 �@
�@
�ɓ������Ȃ�B�@�@
�@�@
�i�����ȏؖ��j
�@�ȉ��̃e�L�X�g�Ɍf�ڂ���Ă��邪�A���Ȃ�ʓ|�B�o�傪����B
�@�@���Y�w��͓���II�xVII�́�4(pp.110-119.);���w��͊T�_�x8��96��(pp.355-359)
�@�@�}���w�����ϕ��w�x7.3�� (pp.266-270);�����w��͓���II�x��7�́�7.3 (pp.355-388.)
�@
�����ڎ��ɖ߂�B
�ϕ��̕ϐ��ϊ��̗�1:�A�t�B��affine�ϊ�
�ϕ��̕ϐ��ϊ��̗�2:�ɍ��W�ϊ�
�����ڎ��ɖ߂�B
(reference)
�}��ᩎi�w�����ϕ��w�x�T�C�G���X�ЁA1974�N�A7.3�� (pp.266-270)�B
���c���r�w21���I�̐��w1:�����ϕ��x�����o�ŁA2002�N�A��10��3��(365-73.)�B
�����M�F�w��͓���II�x (�y����)��g���X�A2003�N�A��7�́�7.3 (pp.355-388.)�B�����ȏؖ����A���X�Ə��q�B
���Y���v�w��͓���II�x������w�o�ʼn�A1980�N�AVII�́�4(pp.106-119.)�B�����ȏؖ����A���X�Ə��q�B
���ؒ厡�w��͊T�_:������3�Łx��g���X�A1983�N�A8��96��(pp.349-359) �B
���c�E�V�ہw���H�n�̔����ϕ��w�x�w�p�}���o�ŎЁA1987�N�Ap.205�B�����ȏؖ��͏ȗ��B�ϐ��ϊ��O��̖ʐϔ䂪���R�r�A���ɂȂ邱�Ƃ𒆐S�ɒ����I�ɐ����B
���`���j�w���H�n���w�̃L�[�|�C���g7:���ϐ��̔����ϕ��x��g���X�A1996�A95-106. �����ȏؖ��͏ȗ��B�ϐ��ϊ��O��̖ʐϔ䂪���R�r�A���ɂȂ邱�Ƃ𒆐S�ɁA�C���[�W���₷�������B
�a�B�O���w���H�n�̐��w����R�[�X1:�����ϕ��x��g���X�A1988�N�App. 145-152;
Lang,Serge.Undergraduate Analysis(Undergraduate
Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg
Tokyo,1983,Chapter 19. Multiple Integrals. (pp.468-482.)�B
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@
�@