一次結合が一次従属となるための十分条件(2)一次結合の個数・一次結合を構成するベクトルの個数と、一次従属
設定
R
:実数体(実数をすべて集めた集合)Rn:実n次元数ベクトル空間
+:実n次元数ベクトル空間Rnに定められたベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:
実n次元数ベクトル空間Rnに定められたスカラー乗法
v1, v2, …, vl:l個の実n次元数ベクトル。
具体的に書くと、
v1= ( v11, v12, …, v1n ) ただし、v11 , v12 , …, v1n ∈R
v2= ( v21, v22, …, v2n ) ただし、v21 , v22 , …, v2n ∈R
: :
vl= ( vl1, vl2, …, vln ) ただし、vl1 , vl2 , …, vln ∈R
したがって、v1, v2, …, vl ∈Rn 。
なお、個数lが有限個であることに注意。
a1, a2, …, al :スカラー。a1, a2, …, al ∈R
[
文献]永田『理系のための線形代数の基礎』補題1.2.1(p.12);
佐武『線形代数学』Ⅲ§1定理1系1(p.90);
命題
1m>l ならば、m個の「v1, v2, …, vlの一次結合」は一次従属。
つまり、
w1=a11v1+a12v2+…+a1lvl (a11, a12, …, a1l ∈R、v1, v2, …, vl ∈Rn )
w2=a21v1+a22v2+…+a2lvl (a21, a22, …, a2l ∈R、v1, v2, …, vl ∈Rn )
:
wm=am1v1+am2v2+…+amlvl (am1, am2, …, aml ∈R、v1, v2, …, vl ∈Rn )
であって、
命題
2実n次元数ベクトルv1, v2, …, vlの一次結合をm個つくる。
m個の「v1, v2, …, vlの一次結合」が一次独立ならば、m≦l。
つまり、
w1=a11v1+a12v2+…+a1lvl (a11, a12, …, a1l ∈R、v1, v2, …, vl ∈Rn )
w2=a21v1+a22v2+…+a2lvl (a21, a22, …, a2l ∈R、v1, v2, …, vl ∈Rn )
:
wm=am1v1+am2v2+…+amlvl (am1, am2, …, aml ∈R、v1, v2, …, vl ∈Rn )
であって、
図解
命題
1と命題2を図解すると、次のようになる。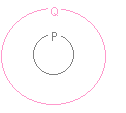
Pの内側:「v1, v2, …, vlの一次結合」w1, w2, …, wmがl個より多い(m>l )
Pの外側:「v1, v2, …, vlの一次結合」w1, w2, …, wmがl個以下(m≦l)
Qの内側:「v1, v2, …, vlの一次結合」w1, w2, …, wmが一次従属
Qの外側:「v1, v2, …, vlの一次結合」w1, w2, …, wmが一次独立
つまり、命題1・命題2が言わんとしていることは、
「v1, v2, …, vlの一次結合」w1, w2, …, wmは、
個数mと一次独立/一次従属に関して、
次の三つのケースのいずれかに分けられるということ。
[case1: 上図のPの内側]
「v1, v2, …, vlの一次結合」w1, w2, …, wmの個数mがl個より多く(m>l )、なおかつ、一次従属
[case2: 上図のPとQのあいだ]
「v1, v2, …, vlの一次結合」w1, w2, …, wmの個数mがl個以下、なおかつ、一次従属
[case3: 上図のQの外側]
「v1, v2, …, vlの一次結合」w1, w2, …, wmの個数mがl個以下、なおかつ、一次独立
この3ケースにわかれるので、
・m>l ならば、case1のみに該当して、w1, w2, …, wmは一次従属(命題1)
・w1, w2, …, wmが一次独立ならば、case3のみに該当して、m≦l (命題2)
とだけ断言できて、
m≦l のときには、一次独立/一次従属に関してなんともいえず、
一次従属のときも、個数についてなんともいえない、
ということになる。
命題
3[佐武『線形代数学』Ⅲ§1定理1系1(p.90);]
「実n次元数ベクトルv1, v2, …, vlの一次結合」をl個つくる。
l個の「v1, v2, …, vlの一次結合」が一次独立ならば、
v1, v2, …, vlも一次独立であり、
v1, v2, …, vlはそれぞれ、l個の「v1, v2, …, vlの一次結合」の一次結合として表せる。
つまり、
w1=a11v1+a12v2+…+a1lvl (a11, a12, …, a1l ∈R、v1, v2, …, vl ∈Rn )
w2=a21v1+a22v2+…+a2lvl (a21, a22, …, a2l ∈R、v1, v2, …, vl ∈Rn )
:
wl=al1v1+al2v2+…+allvl (al1, al2, …, all ∈R、v1, v2, …, vl ∈Rn )
であって、
v1, v2, …, vlも一次独立であり、
v1=b11w1+b12w2+…+b1lwl (b11, b12, …, b1l ∈R、w1, w2, …, wl ∈Rn )
v2=b21w1+b22w2+…+b2lwl (b21, b22, …, b2l ∈R、w1, w2, …, wl ∈Rn )
:
vl=bl1w1+bl2w2+…+bllwl (bl1, bl2, …, bll ∈R、w1, w2, …, wl ∈Rn )
と表せる。
命題
1の
証明
・
w1, w2, …, wl, w(l+1)は一次従属。(∵)・w1, w2, …, wl, w(l+1)が一次従属であって、m>l ならば、
w1, w2, …, wl, w(l+1),w(l+2), …, wmは一次従属。 (∵)
[
文献]永田『理系のための線形代数の基礎』補題1.2.1(p.12);
命題
2命題3
の
証明
実n次元数ベクトルの有限集合の基底の存在を、
{ w1, w2, …, wm } + {v1, v2, …, vl } に適用する。
[
文献]佐武『線形代数学』Ⅲ§1定理1系1(p.90);