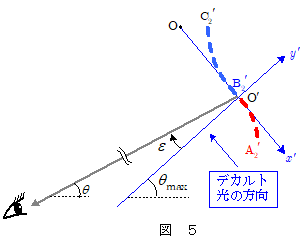
雨滴内で屈折と反射をして雨滴外に出てきた波面が図5の波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ で置き換えられ,その式が $x'$ の3次曲線として $\maru{4}$ 式のように近似できるとして,以下に話を進めます。 \[ y' = -\bun{h}{3a^2}x{}'\,{}^3 \quad\quad\cdots\cdots\maru{4} \\ \kern-1em \bigg( ただし,\ h=\bun{9}{4(n^2 - 1)}\kon{\bun{4 - n^2}{n^2 - 1}}\quad \bigg ) \]
ここで波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ から,デカルト光方向から時計回りに測った角 $\varepsilon$ の方向(太陽光の入射方向から測った散乱角 $\theta = \theta_{max} - \varepsilon$ )に射出された光波の合成波の振幅を求めていきます。観測者は雨滴より十分遠方に離れていますから,波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ から同じ角方向に出た光はすべて重なっていると考えることができます。
この場合,波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ 上の各点から発した2次波の位相差を考慮した上で,波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ 全体にわたって光波を積分していくわけですが,その積分が『エアリー(George Airy)の虹積分』と呼ばれるものになります。
結果だけを示せば,以下のようになります。(詳細は こちら )
光波の波長を $\lambda$ とし,以下の新しい2つの変数 $u$ , $z$ を用意します。 \[u =\bigg ( \bun{4h}{3a^2 \lambda} \cos \varepsilon \bigg ) ^{1/3}\times x' \quad\cdots\cdots\maru{5} \\ z = \bigg ( \bun{48 a^2}{h \lambda^2}\sin^2\varepsilon \cdot \tan\varepsilon \bigg)^{1/3} \quad\cdots\cdots\maru{6} \] これらの変数 $u$ , $z$ を用いて,角 $\varepsilon$ 方向への合成光波の振幅 $A$ は, \[A = 2k \bigg ( \bun{3a^2 \lambda }{4h \cos\varepsilon} \bigg )^{1/3} \times \int _0^\infty \cos \bun{\pi}{2}(u^3 - z \, u) du \] ここで $k$ は,全体の光の強さに係る比例定数です。よって,\[f(z) = \int _0^\infty \cos \bun{\pi}{2}(u^3 - z \, u) du \quad\cdots\cdots\maru{7} \\ M = 2k \bigg ( \bun{3a^2 \lambda }{4h \cos\varepsilon} \bigg )^{1/3} \quad\cdots\cdots\maru{8} \]とおくと,光の強度 $I$ は合成光波の振幅の2乗に比例するので,\[I \propto A^2 = M^2\,f^2(z) \quad\cdots\cdots\maru{9}\]となります。
$\maru{7} \sim \maru{9}$ 式が虹の光強度を与える式になるわけですが,具体的にどのような光強度分布になりどのような虹が見えるのか,これらの式が持つ物理的意味と虹の特徴について次の項で説明します。
解説10(波動光学による虹)
虹の話
概要
解説1(解説1:雨滴による虹散乱)
解説2(虹の色と散乱角)
\mu解説3(散乱角の詳細計算)
解説4(反射率)
解説5(虹散乱での反射率)
*** 以下,過剰虹 関連 ***
解説6(波動光学)
解説7(過剰虹成因の概要)
解説8(波面の式)
解説9(虹の光強度の式)
解説10(波動光学による虹)