これまでの議論はすべて, 音源速度 $v$ や観測者速度 $u$ が音速 $V$ より小さいという前提で論じてきた( $v < V$ , $u < V$ )。
では,これらの速度が音速を超えた場合はどうなるのだろうか?
下の図16は,本ホームページ内の『波のシミュレーション』というページにおいて,媒質中で波源を移動させたときの波の様子を示す画像です。(Javaアプレット仕様。このシミュレーションでは波の式は一切使っておらず,すべて媒質中の各点に力学的な振動を与えたとして,力学的な数値解析によりシミュレートしたものになっています。)
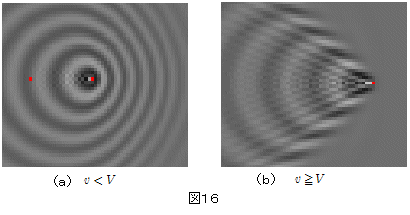
上図の(a)は $v < V$ の場合である。波源(右側の赤い小さな点)前方での波長が狭く,後方での波長が広くなっており,ドップラー効果が起きていることを示している。
(b)は $v \ge V$ の場合であり,濃淡の濃い部分が波源を頂点とした三角形の2辺を成すように広がっている。この濃淡の濃い部分は,媒質の密度変化が極めて大きくなっていることを示す。水面上を進む船の舳先(へさき)にもこのような波ができていることがあるが,このとき 船の速さ>水面を伝わる波の速さ となっているためである。
もしこの波が音波であるとすれば,この部分の空気圧は急激に変化していることになる。これが空気中を伝って地上に下りてくれば,爆風のような急激な圧力変動が起こり,窓ガラスが割れたりするようなことも起こる。これが衝撃波である。
このように $v < V$ であれば衝撃波は発生しないが, $V$ を超えようとするとき,音波の場合であれば音速を超えようとするとき(マッハ1以上),衝撃波(ソニックブーム)が発生する。雷鳴や隕石落下時の大音響(空気の大振動)なども,音源がマッハ1以上の速さで空気中を移動することによって発生する衝撃波である。
衝撃波とは読んで字の如く「波」であり,空気中を伝わる波は圧力変化(つまり音波)であるから,直接目で確かめることはできない。
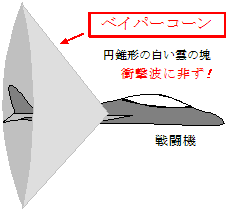
ネット上には「衝撃波」と称して,下図のような,円錐形の白い雲の塊を高速のジェット機が突き破っているような動画や画像があるが,これは「ベイパ-コーン」と呼ばれる「雲」であって,音速以下でも発生し得る。高速で運動する機体の前面では空気が極度に圧縮され,その直後に今度は空気の急膨張が起こる。この膨張は断熱膨張であり,温度が急低下する。このときこの空気が適当量の水蒸気を含んでいると,気温低下に伴う水蒸気の凝縮が起き,雲を発生するのである。機体の速度が大きいほど空気の圧縮は大きいのでベイパ-コーンは出来やすくなることは確かであるが,音速を超える超えないということとは,直接には関係のない話である。
衝撃波は波であり,これを目で直接確認することはできないが,空気の密度変動に伴う光の屈折率変化として間接的に(視覚的に)捉えた貴重な映像がある。アメリカのアトラスロケット打ち上げ時の映像で,ロケットがマッハを超えたと思われる時点で,突然上空に浮かんでいた雲が波打ち始め,これが同心円状に広がっていく様子が映っている。感動的ですので,是非ご覧ください。
アトラスロケットのソニックブーム
$v > V$ の場合として,図17のような衝撃波ができているときを考えよう。
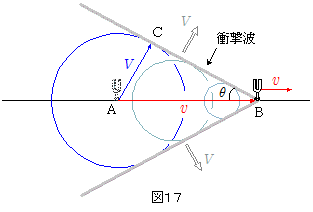
点Aで音源から出された音波は,風がなければ,単位時間後には点Aを中心として半径 $V$ の円形(球面)状に広がっている。一方この間に音源は点Aの前方,距離 $v$ の点Bに達している。 $v > V$ であるから,Bの位置は半径 $V$ の円の外にある。音源がAからBに移動する間音波を出し続けているので,これらの円形(球面)波の共通接面のところに衝撃波ができている。よって衝撃波が音源の進行方向となす角 $\theta$ は,次式を満たす。これより角 $\theta$ が分かれば,音源速度 $v$ を知ることができる。\[\sin\theta = \bun{V}{v} \]