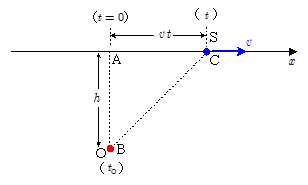
上図のように, $x$ 軸上を振動数 $f$ の音波を発する音源が速度 $v$ で運動しており, $x$ 軸と距離 $h$ 離れた位置Bに観測者Oが静止している。このとき観測者が観測する音波はどのように変化するか,音波の振動の式を時刻の関数として求めてみよう。
音源が図の点Aを通過したときを時刻 $0$ とし,音源からは点Aに達する以前から音波が出し続けられていたものとする。音源から発せられる音波の振動は,時刻 $t$ の関数として,\[y_\mathrm{S}=A\sin(2 \pi f\, t) \cdots\cdots\maru{1} \]と表されるとする。
いま時刻 $t$ に音源Sは点Cを通過し,この位置で出された音波が時刻 $t_\mathrm{O}$ に観測者Oに届いたものとする。このとき $t_\mathrm{O}$ と $t$ の関係は,音波の伝播時間を考慮して,\[t_\mathrm{O} = t + \bun{\overline{\mathrm{BC}}}{V} \\ \quad = t + \bun{\kon{h^2+(v\,t)^2}}{V} \\ \therefore V^2(t_\mathrm{O}-t)^2 = h^2+(v\,t)^2 \\ \therefore (V^2-v^2)t^2 - 2V^2\,t_\mathrm{O} \cdot t +V^2\,t_\mathrm{O}{}^2 - h^2 = 0 \\ \therefore t=\bun{V^2}{V^2-v^2}t_\mathrm{O} - \bun{\kon{(V^2-v^2)h^2 + (V\, v\, t_\mathrm{O})^2}}{V^2-v^2} \cdots\cdots\maru{2} \\ \quad (ただし,t_\mathrm{O}>t )\] 観測者が時刻 $t_\mathrm{O}$ に聴く音は音源を時刻 $t$ に出た音であるから, $\maru{2}$ 式の $t$ を $\maru{1}$ 式に代入したものが,時刻 $t_\mathrm{O}$ に観測者が聴く音波・・・ということになる。\[ \kern-2em y_\mathrm{O} = A\sin2\pi f t \quad\quad\quad\cdots\cdots\cdots\cdots\cdots\maru{3}\\ =A\sin 2\pi f\bigg(\bun{V^2}{V^2-v^2}t_\mathrm{O} - \bun{\kon{(V^2-v^2)h^2 + (V \, v \, t_\mathrm{O})^2}}{V^2-v^2} \bigg) \cdots\cdots\maru{4} \] 本シミュレーションは,上記 $\maru{4}$ で表される振動をMathematicaという数学ソフトを使ってsoundソースを作成し,これを再生できるようにしたものである。この場合近似などの前提条件等は一切仮定しておらず,したがって観測者が時刻 $t_\mathrm{O}$ に観測するであろう振動を正しく表していることになる。
$v=0$ ,すなわち音源が点Aで静止したまま振動音を発しているとき,観測者が観測する振動音は,上式に$v=0$ を代入して,\[y_\mathrm{O} = A\sin2\pi f \bigg( t_\mathrm{O} - \bun{h}{V}\bigg) \\ \quad = A\sin2\pi \bigg(f t_\mathrm{O}-\bun{h}{V/f}\bigg) \cdots\cdots\maru{5} \]となる。このとき音源も観測者も静止しているのだからドップラー効果は起きておらず,振動数 $f$ の振動音が観測されることになる。第2項 $\bun{h}{V/f}$ は,点Aと観測点Bが距離 $h$ だけ離れていることに起因する項である。
音源が点Aで静止している( $v=0$ )とき点Bの観測者Oが聴く音波は $\maru{5}$ で与えられ,音源が運動している( $v\ne 0$ )とき観測者が聴く音波は式 $\maru{3}$ (すなわち $\maru{4}$ 式)で与えられる。
ところで正弦振動の場合,sin の中身で時間とともに変化する位相部分, $\maru{5}$ 式の場合なら $2\pi ft_\mathrm{O}$ , $\maru{3}$ 式の場合なら $2\pi f\,t$ が $2\pi$ 増加するごとに1回振動するわけであるから, $ ft_\mathrm{O}$ もしくは $ f\,t$ の値が1秒間に $n$ だけ増加すれば音波は $n$ 回振動することとなり,振動数 $n$ の音波として観測されることになる。したがってもし, $ f\,t$ の増加の仕方が $ ft_\mathrm{O}$ の増加の仕方の2倍なら, $\maru{3}(=\maru{4})$ 式で表される音波の振動数は $\maru{5}$ 式で表される音波の振動数 $f$ の2倍ということになるだろう。
以上より分かるように,振動数は位相の時間変化のスピード,したがって$ 2\pi f\,t$ および $2 \pi f\,t_\mathrm{O}$ が時間変化する速度で決まることになる。
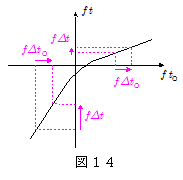
$f\,t$ と $f\,t_\mathrm{O}$ 関係は,およそ図14のグラフのようになる。
上で述べたように,振動数を比較するには,$f\,t$ と $f\,t_\mathrm{O}$ の「変化の速さ」を比較していけばよい。ここで原音の振動数 $f$ は定数として扱ってよいことを考えると,振動数の比較には, $t_\mathrm{O}$ の「変化の速さ」に対して $t$ の「変化の速さ」が何倍になっているかを知ればよいことになる。すなわち $t_\mathrm{O}$ の増分 $\varDelta t_\mathrm{O}$ に対する $t$ の増分 $\varDelta t$ の割合, $\varDelta t/\varDelta t_\mathrm{O}$ が分かればよいことになる。この値は $\maru{2}$ 式で表される $t$ を $t_\mathrm{O}$ で微分することによって得られる。\[\kern-2em \dif{t}{t_\mathrm{O}}= \bun{1}{V^2-v^2}\bigg\{V^2 - \bun{V^2\,v^2\,t_\mathrm{O}}{\kon{(V^2-v^2)h^2+(V\,v\,t_\mathrm{O})^2}} \bigg\} \]
音源が静止している( $v=0$ )ときの音波の式は $\maru{5}$ 式で表され,このとき観測される振動数は $f$ であるから, $\maru{3}$ 式もしくは $\maru{4}$ 式で表される音波の振動数を $F$ とすると,\[\kern-2em \bun{F}{f} = \bun{\maru{3}の位相変化速度}{\maru{5}の位相変化速度} = \bun{2\pi f\cdot\varDelta t}{2\pi f\cdot\varDelta t_\mathrm{O}} \Rightarrow \dif{t}{t_\mathrm{O}} \\
\kern-2em \therefore F = \bun{\mathrm{d}t}{\mathrm{d}t_\mathrm{O}} \times f \\ \kern-1em \color{red}{= \bun{1}{V^2-v^2}\bigg\{V^2 - \bun{V^2\,v^2\,t_\mathrm{O}}{\kon{(V^2-v^2)h^2+(V\,v\,t_\mathrm{O})^2}} \bigg\} \times f } \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \cdots\cdots\maru{6} \]
上式が,観測時刻 $t_\mathrm{O}$ と観測振動数 $F$ の関係を示す厳密解である。 その関係は,図15のグラフのようになる。
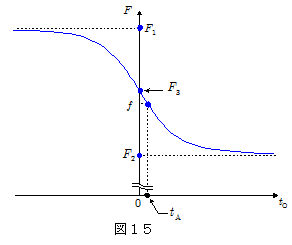
◎ $F_1$ ,$F_2$ はそれぞれ$\maru{6}$ 式に $t_\mathrm{O}=-\infty$ ,$t_\mathrm{O}=+\infty$ を代入したときの振動数で,$F_1$ は音源が十分遠方から点Aに向かって近づいてくる場合の,$F_2$ は音源が点Aから十分遠方に遠ざかった場合の振動数にあたる。
◎ $F_3$ は時刻 $t_\mathrm{O}=0$ ,すなわち音源がちょうど点Aを通過する瞬間に観測点Bで観測される振動数で, $\maru{6}$ 式に $t_\mathrm{O}=0$ を代入すればよい。
◎ 音源が点Aを通過時に出した音波は,伝播時間を考慮すれば,観測点Bには時刻 $t_\mathrm{A}=h/V$ に届く。 $\maru{6}$ 式の $t_\mathrm{O}$ にこの時刻を代入すると, $F = f$ となり,点A通過時に出された音波が観測点Bに届いたときドップラー効果が起きていないことを示す。これは,点A通過時において,音源速度の視線成分が $0$ になっていることの裏付け,とも言える。
以上をまとめると,\[ \left \{ \begin{array}{rl}
& \kern-1em F_1=\bun{V}{V-v}f \\
& \kern-1em F_2=\bun{V}{V+v}f \\
& \kern-1em F_3=\bun{V^2}{V^2-v^2}f \\
& \kern-1em t_\mathrm{A}=\bun{h}{V}
\end{array} \right . \]となる。とくに,時刻 $t_\mathrm{O}=0$ に聴く振動数 $F_3$ は,A・B間の距離 $h$ に無関係な値となり ,\[F_3=\bun{V^2}{V^2-v^2}f \\ \quad = \bun{1}{2}\bigg(\bun{V}{V-v}f+\bun{V}{V+v}f\bigg) \\ \quad = \bun{F_1+F_2}{2} \quad(←F_1 とF_2 の中間値) \]となっている点に注目したい。
◎ 衝 撃 波 に続く。