(1) 波源が動く効果
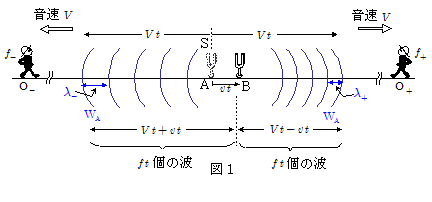
図1において,図の右向きに速さ $v$ で運動している音源Sがある。この音源からは振動数 $f$ の音波が常時発せられているとする。音速を $V$ とし, $V>v$ の関係があるとする。また,風はないとする。
この音源が,図の点Aを通過した時刻を時刻 $0$ とし,時刻 $t$ に点Bを達したとする。この間にこの音源から発せられた音波の数は前方,後方ともにそれぞれ $f t$ 個ずつであり,時刻 $t=0$ に点Aで発せられた音波は点Aからはかって距離 $Vt$ の前方および後方の位置 $\mathrm{W_A}$ にまで広がっている。一方この間にこの音源は図の右方に距離 $v \,t$ 進んでいるので,音源の前方(図の右方)では距離 $Vt-v\,t$ の距離内に $f\,t$ 個の波があり,音源の後方(図の左方)では距離 $Vt+v\,t$ の距離内に $f\, t$ 個の波が含まれていることになる。したがって音源の前方に進む音波の波長 $\lambda_+$, 後方に進む音波の波長 $\lambda_-$は,波の含まれている距離を波の数で割って,それぞれ,\[
\left \{ \begin{array}{rl}
& \kern-1em \lambda_+= \bun{Vt-v\,t}{f\, t} = \bun{V-v}{f} \cdots\cdots\maru{1}\\
& \kern-1em \lambda_-= \bun{Vt+v\,t}{f\, t} = \bun{V+v}{f} \cdots\cdots\maru{2}
\end{array} \right . \]となる。このように,音源が動くことによって波長が変化する。
よって,音源の前方に観測者 $\mathrm{O_+}$ が,後方に観測者 $\mathrm{O_-}$ が静止しているとすれば,これらの観測者が聴く音波の振動数 $F_+$ ,$F_-$は,それぞれ,\[
\left \{ \begin{array}{rl}
& \kern-1em F_+=\bun{V}{\lambda_+} = \bun{V}{V-v}f \cdots\cdots\maru{3}\\
& \kern-1em F_-=\bun{V}{\lambda_-} = \bun{V}{V+v}f \cdots\cdots\maru{4}
\end{array} \right . \]となる。これが,音源が動き,観測者が静止している場合の振動数を与える式である。
ところで $\maru{1}$ 式中の $V-v$ , $\maru{2}$ 式中の $V+v$ は何を意味するだろうか?
音源の前方および後方に進む音波はもちろん空気中を音速 $V$ で広がっていきますが,音源が速さ $v$ で移動するため,音源から見ると音波は,前方へは相対的に $V-v$ の速さで,後方へは相対的に $V+v$ の速さで広がっていくように見える筈です。すなわち $\maru{1}$ 式 , $\maru{2}$ 式中の分子は,音源が動くことによって生じる音源から見た相対的な音速を意味することになります。よって,\[\color{red}{波長=\bun{音源に対する相対的な音速}{音源の振動数}}\]
となります。このように,音源が動くことによって音源に対する相対的な音速が変わり,そのために波長が変化するわけです。
【参考】上記の関係を,波の式を使って示してみよう。
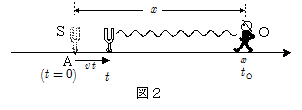
波源Sから \[y_\mathrm{S}=A\sin(2\pi f t) \cdots\cdots\maru{5} \] で表される音波が発せられているとする。ここで $A$ は振幅, $f$ は振動数, $t$ は時刻である。この音源が $x$ 軸上の点Aを時刻 $0$ に通過し,その後音波を出し続けているとする。この音波を音源の前方,点Aから測って距離 $x$ の位置に観測者Oが静止していて,この音波を観測していたとする。
音源Sが時刻 $t$ に発した音波が観測者Oに時刻 $t_\mathrm{O}$ に届いたとすると,観測者Oがこの時刻 $t_\mathrm{O}$ に聞く音は音源Sを時刻 $t$ 出た音波・・・ということになる。この $t_\mathrm{O}$ と $t$ の関係が分かれば,観測者Oが聴く音がどのように変化していくかが分かることになる。ここで,\[
t_\mathrm{O}=音波がSを出た時刻 + 伝播時間 \\ \quad =t + \bun{x-v\,t}{V}\cdots\cdots\maru{6} \\ \quad = \bun{V-v}{V}t + \bun{x}{V} \\ \therefore t=\bun{V}{V-v}t_\mathrm{O}-\bun{x}{V-v} \]
観測者Oが時刻 $t_\mathrm{O}$ に聞く音は音源を時刻 $t$ に出た音であるのだから, $\maru{5}$ 式の $t$ に $\maru{6}$ 式の $t$ を代入すれば,観測者Oが時刻 $t_\mathrm{O}$ に聞く音波の式が求まることになる。\[\therefore y_\mathrm{O}=A\sin2\pi f\bigg(\bun{V}{V-v}t_\mathrm{O}-\bun{x}{V-v} \bigg)\ \\ \quad =A\sin2\pi \bigg(\bun{V}{V-v}f \cdot t_\mathrm{O} - \bun{f}{V-v}x\bigg) \\ \quad =A\sin2\pi \bigg(\bun{V}{V-v}f \cdot t_\mathrm{O} - \bun{x}{(V-v)/f} \bigg) \cdots\cdots\maru{7} \] この式と進行波の一般式 $y=A\sin2\pi \bigg(f\,t - \bun{x}{\lambda}\bigg)$ とを比較すると,観測者Oが音波を観測したとき,\[
\left \{ \begin{array}{rl}
& \kern-1em 振動数 F=\bun{V}{V-v}f \\
& \kern-1em 波長 \lambda'=\bun{V-v}{f}
\end{array} \right . \]
の波として観測されることが分かる。この結果は,前記 $\maru{3}$ 式, $\maru{1}$ 式と同じである。逆向きに進む波値ついては $v$ を $-v$ とすれば,前記 $\maru{4}$ 式, $\maru{2}$ 式と同じ結果を得る。
以上の考え方でポイントとなるのは,音波が音源を出た時刻 $t$ と,この音波が観測者に届く時刻 $t_\mathrm{O}$ との関係を示す $\maru{6}$ 式である。 \[ \kern-2em \color{red}{ 観測者が波を受け取る時刻 = \\ \quad\quad\quad\quad 音波が音源を出た時刻 + 音波の伝播時間 } \]
上記の右辺第2項『音波の伝播時間』が,音源が動く場合と観測者が動く場合によって異なる形となり,その結果,それぞれに特徴的なドップラー効果が現れることになるのである。
(2)観測者が動く効果 に続く。