(2) 観測者が動く効果
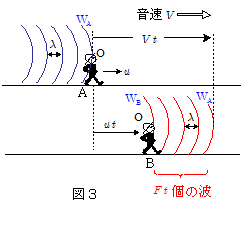
図3において,観測者Oが図の右向きに速さ $u$ で運動している。この観測者の後ろから波長 $\lambda$ の音波が音速 $V\,(>v\,)$ で追い越していく場合を考える。このとき,観測者が動こうが止まっていようが,波長は観測者の動きに関係なく,一定している。
いま,観測者が図の点Aを通過したときを時刻 $0$ とし,この瞬間に音波の波面 $\mathrm{W_A}$ がまさに観測者を追い越そうとしていたとする。その後時間 $t$ の間に観測者は $u\, t$ だけ進み,点Bに達していたとする。この間に波面 $\mathrm{W_A}$ は距離 $V\,t$ だけ進んでいるので,この間に観測者を追い越した音波の波面は $V\,t - u\,t$ の距離内にある音波ということになる。音波の波長 $\lambda$ は変化しないのだから,観測者を追い越した音波の数は $\bun{V\,t - u\,t}{\lambda}$ と表されるはずである。
一方この観測者が観測する音波の振動数を $F$ とすると,振動数は単位時間内の振動回数(→観測者を追い越した波の数)であるから,この時間 $t$ 内に観測者が観測する音波の数は $F\,t$ である。
以上2つの式を結びつけると,\[F\,t = \bun{V\,t - u\,t}{\lambda} \\ \therefore F=\bun{V-u}{\lambda} \cdots\cdots\maru{1}
\]
観測者が音波のやってくる方に向かって運動する場合は,上式の $u$ を $-u$ とおけばよいので,\[F=\bun{V-(-u)}{\lambda} = \bun{V+u}{\lambda} \cdots\cdots\maru{2}
\]
となる。
【参考】上記の関係を,波の式を使って示してみよう。
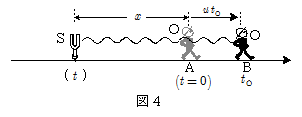
静止している波源Sから \[y_\mathrm{S}=A\sin(2\pi f t) \cdots\cdots\maru{3} \] で表される音波が発せられているとする。この波源の前方距離 $x$ のところに観測者Oがいて,時刻 $t=0$ より,音源方向と逆向きに速度 $u$ で歩き出したとする。このとき時刻 $t$ に音源を出た音波が時刻 $t_\mathrm{O}$ に観測者Oに達したとして, $t_\mathrm{O}$ と $t$ の関係を調べてみる。\[t_\mathrm{O} = 音源を出た時刻 + 伝播時間 \\ \quad = t + \bun{x+u\,t_\mathrm{O}}{V} \\ \therefore t = \bun{V-u}{V}t_\mathrm{O} - \bun{x}{V} \] 観測者Oが時刻 $t_\mathrm{O}$ に聴く音は,音源を時刻 $t$ に出た音波であるから,上記の $t$ を $\maru{3}$ 式に代入して,\[y_\mathrm{O}=A\sin2\pi f \bigg( \bun{V-u}{V}t_\mathrm{O} - \bun{x}{V}\bigg) \\ \quad =A\sin 2\pi \bigg(\bun{V-u}{V}f\cdot t_\mathrm{O} - \bun{f}{V}x \bigg) \] 上式と波の一般式 $y=A\sin\bigg(f\,t - \bun{x}{\lambda}\bigg)$ とを比べると,この場合に観測者Oが観測する音波は,\[ \left \{ \begin{array}{rl} & \kern-1em 振動数 F= \bun{V-u}{V}f \\ & \kern-1em 波長 \lambda = \bun{V}{f} \end{array} \right . \\ \therefore F= \bun{V-u}{V}f = \bun{V-u}{\lambda} \] の波として観測していることが分かる。
(3)音源と観測者が動く場合 に続く。