(3) 音源と観測者が動く場合
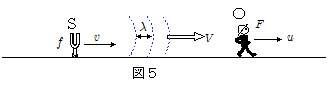
図5のように,振動数 $f$ の音源Sが速度 $v$ で,観測者Oが速度 $u$ で,ともに同じ向きに進んでいる場合について考える。ただし音速 $V$ に対して, $v < V$ , $u < V$ の関係があるものとする。
このとき,音源より発せられた音波の波長 $\lambda$ は,前項(1)『波源が動く効果』の $\maru{1}$式より,\[\lambda=\bun{V-v}{f}\]である。またこのとき観測者が観測する音波の振動数 $F$ は, 前項(2)『観測者が動く効果』の $\maru{1}$式より,\[F=\bun{V-u}{\lambda} \]である。よってこの2式より $\lambda$ を消去すれば,音源・観測者の双方が運動する場合に観測される音波の振動数が求まる。
\[F=\bun{V-u}{\lambda}=\bun{V-u}{V-v}f \\ \therefore \bun{F}{f} = \bun{V-u}{V-v} \] 音源,観測者が逆向きに運動する場合は,それぞれ $-v$ , $-u$ と置き換えればよい。
ところで $V-v$ , $V-u$ はそれぞれ音源から見た相対的な音速,観測者から見た相対的な音速であった。よって上式より,振動数の比は相対音速の比に等しい・・・ということが言える。
これより,ドップラー効果の振動数の公式は以下のように覚えておくとよい。
≪ドップラー効果の公式の覚え方≫
\[\bun{f_\mathrm{O}}{f}=\bun{V-u}{V-v} \\ \kern-2em \Rightarrow \color{red}{\bun{観測者が聴く振動数}{音源が出す振動数} = \bun{観測者に対する音速}{音源に対する音速} \\ ただし,S→Oの向きの速度を正とする。 } \]
【参考】再度,上記の関係を波の式を使って確認してみよう。
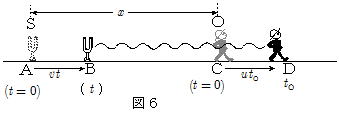
図の右向きにそれぞれ速度 $v$ , $u$ で運動する音源Sと観測者Oがある。音源からは常時, \[y_\mathrm{S}=A\sin(2\pi f t) \cdots\cdots\maru{1} \] で表される音波が発せられている。
時刻 $0$ に音源,観測者は距離 $x$ 離れた点A,Cを通過したとして,時刻 $t_\mathrm{O}$ に観測者が聴く音波について考える。この音波は音源から時刻 $t$ に発せられた音波とすれば,\[t_\mathrm{O}=音源を出た時刻 + 伝播時間 \\ \quad = t + \bun{\mathrm{BD}}{V} \\ \quad = t + \bun{x - v\,t + u \, t_\mathrm{O}}{V} \\ \therefore \bun{V-u}{V}t_\mathrm{O} = \bun{V-v}{V}t + \bun{x}{V} \\ \therefore t = \bun{V-u}{V-v}t_\mathrm{O} - \bun{x}{V-v} \] この $t$ を $\maru{1}$ 式の $t$ に代入すれば,時刻 $t_\mathrm{O}$ に観測者が聴く音波ということになる。\[y_\mathrm{O}=A\sin2\pi f \bigg(\bun{V-u}{V-v}t_\mathrm{O} - \bun{x}{V-v}\bigg) \\ \quad = A\sin 2\pi\bigg(\bun{V-u}{V-v}f\cdot t_\mathrm{O} - \bun{f}{V-v}x\bigg) \]
上式と波の一般式 $y=A\sin\bigg(f\,t - \bun{x}{\lambda}\bigg)$ とを比べると,この場合に観測者Oが観測する音波は,\[
\left \{ \begin{array}{rl}
& \kern-1em 振動数 F = \bun{V-u}{V-v}f \\
& \kern-1em 波長 \lambda = \bun{V-v}{f}
\end{array} \right . \]
であることが分かる。
◎斜めに動く場合 に続く。