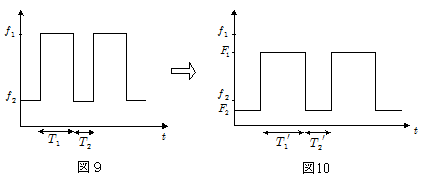
図9のように,振動数 $f_1$ と $f_2$ の音を交互に,それぞれ時間 $T_1$ , $T_2$ ずつ出す音源があり,この音源の音が,音源・観測者の移動によって,振動数 $F_1$ と $F_2$ の音として,交互にそれぞれ時間 $T_1\,'$ , $T_2\,'$ ずつ観測されたとする。この場合, $T_1\,'$ , $T_2\,'$ と $T_1$ , $T_2$ の関係はどのようなものであるか・・・というのが本項のテーマである。
基本的な考え方は,音波が途中で消えたり生じたりしないはずであるから,音源から出された音波の総数と,観測者が受け取る音波の総数が等しいということである。
音源からの発信総波数=観測者の受信総波数
よってたとえば上図の場合, 振動数 $f_1$ の音波が時間 $T_1$ の間放出されれば,この間に放出された振動数 $f_1$ の音波の総数は $f_1T_1$ ,またこの音波が振動数 $F_1$ の音波として時間 $T_1\,'$ 間観測されたとすれば,この間に観測された音波の総数は $F_1T_1\,'$ であるから,これらが等しいとおいて,\[f_1T_1=F_1T_1\,' \quad\therefore T_1\,' = \bun{f_1}{F_1}T_1 \]同様に振動数 $f_2$ の音波についても,\[ f_2 T_2=F_2 T_2\,' \quad\therefore T_2\,'=\bun{f_2}{F_2}T_2 \]となる。つまり,ドップラー効果によって振動数が変化するとき,その振動数の音の継続時間は振動数の逆比に比例する,ということになる。
◎風がある場合のドップラー効果:
(1) 1次元方向に風が吹く場合
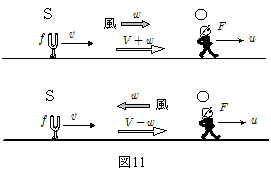
ドップラー効果による振動数の変化は,音源や観測者が運動することによってそれぞれに対する相対的な音速が違ってくることによって生じるこを先に述べた。たとえば上図のように,音源,観測者が図の向きに速度 $v$ , $u$ で運動している場合,風がなければ,音速を $V$ として,\[\bun{F}{f}=\bun{V-u}{V-v} \]で与えられた。
ここで,風速 $w$ の風がある場合,風下側に向かう音波は風に乗って風速の分だけ速く伝わるので,音速を $V+w$ とおけばよい。また逆に,風上側に向かう音波は風に押し戻される形になるので風速の分だけ遅くなり,音速を $V-w$ とおけばよい。よって観測者が,\[\color{red}{風下側にいるとき: 音速 V\,' = V+w \\ 風上側に入るとき: 音速 V\,' = V-w } \] として扱っていけばよいことになる。たとえば図11の場合,\[上の図: \bun{F}{f}=\bun{(V+w)-u}{(V+w)-v} \\ 下の図: \bun{F}{f}=\bun{(V-w)-u}{(V-w)-v} \]
となる。
(2) 斜め方向に風が吹く場合
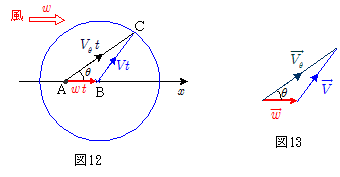
図12のように, $x$ 軸方向に風速 $w$ の風があり,この風に対して角 $\theta$ の方向に伝わる音速 $V_\theta$ はどのように表されるだろうか。
時刻 $0$ に $x$ 軸上の点Aで音源から出た音波が時間 $t$ の後に $x$ 軸に対して角 $\theta$ をなす点Cに達したとする。この間に,点Aから広がり始めた音波は,広がりながら全体が風下側に流されていくので,時刻 $t$ には $\mathrm{AB}=w\,t$ なる点Bを中心とした半径 $Vt$ の円形(球面)状に広がっているはずである。よってこのときA→C方向の音速を $V_\theta$ とすれば,点Aから出た音波が時間 $t$ をかけてA・C間を伝わってきたのであるから, $\mathrm{AC}=V_\theta\,t$ と表させる。以上より図12のような関係が得られ,さらに時間 $t$ を消去すれば図13のような速度のベクトル図が描ける。これに余弦定理を適用することにより,\[V^2=V_\theta{}^2+w^2-2V_\theta\cdot w\cdot \cos\theta\]これを解くことによって $\theta$ 方向に伝わる音速 $V_\theta$ を求めることができる。この $\theta$ を用いてドップラー効果の式を立てていけばよい。
◎本シミュレーションの場合 に続く。