(1) 音源が動く場合
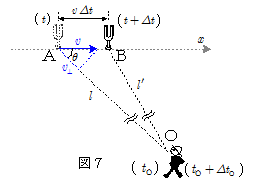
図7のように, $x$ 軸上を速度 $v$ で運動している音源S(振動数 $f$ )があり,その音波を $x$ 軸の外の点Oに静止している観測者が観測しているとする。音速は $V\,\,(\, > \,v\,\,)$ とする。
音源は時刻 $t$ に$x$ 軸上の点Aを通過し,この位置で発した音波が時刻 $t_\mathrm{O}$ に観測者に届き,さらにその微小時間後の時刻 $t+\varDelta t$ に音源は点Bに達し,この位置で発した音波が時刻 $t_\mathrm{O} + \varDelta t_\mathrm{O}$ に観測者に届いたとする。このとき,音源から時間 $\varDelta t$ の間に出された音波は,観測者には時間 $\varDelta t_\mathrm{O}$ の間に聞こえたことになる。
直線AOが $x$ 軸となす角を $\theta$ ,A-O間の距離を $l$ , B-O間の距離を $l\,'$ とすると,このとき,\[
\left \{ \begin{array}{rl}
& \kern-1em t_\mathrm{O}=t+\bun{l}{V} \\
& \kern-1em t_\mathrm{O}+\varDelta t_\mathrm{O}=t+\varDelta t+\bun{l\,'}{V}
\end{array} \right . \\
\therefore \varDelta t_\mathrm{O} = \varDelta t + \bun{l\, '}{V} - \bun{l}{V} \cdots\cdots\maru{1} \]
ここで $\triangle\mathrm{ABO}$ に余弦定理を適用すると, $\overline{\mathrm{AB}}=v\varDelta t$ であるから,\[l\, '=\kon{l^2 +(v\varDelta t)^2 - 2l \cdot v\varDelta t \cdot \cos\theta} \\
\quad = l\bigg\{ 1 + \bigg(\bun{v\varDelta t}{l}\bigg)^2 - 2\bun{v\varDelta t}{l}\cos\theta\bigg\}^{1/2} \cdots\cdots\maru{2} \]
となる。
いま,もし $v\varDelta t \ll l$ の関係があるとして(*注.後述),上式において $\bun{v\varDelta t}{l}$ の2次の項が他の項に対して無視でき,さらに $|x| \ll 1$ のとき成り立つ近似式\[(1 + x)^n \kinji 1 + n\,x\]
が適用できるとすれば,上式の $l\,'$ は,\[l\,' \kinji l\bigg(1 - 2\bun{v\varDelta t}{l}\cos\theta\bigg)^{1/2} \\ \quad \kinji l\bigg(1 - \bun{1}{2}\cdot \bun{2v\varDelta t}{l}\cos\theta\bigg) \\ \quad = l - v\varDelta t \cdot \cos\theta \cdots\cdots\maru{3} \]
となる。
よってこのとき $\maru{1}$ 式は,\[\varDelta t_\mathrm{O} = \varDelta t + \bun{l\, ' - l}{V} \\ \quad = \varDelta t + \bun{(l - v\varDelta t\cdot \cos\theta) - l}{V} \\ \quad = \bun{V-v\cos\theta}{V}\varDelta t \]
となる。
ここで振動数 $f$ の音源からは単位時間当たり $f$ 個の音波が送り出されているので,時間 $\varDelta t$ の間に音源から送り出された音波の数は $f\varDelta t$ であり,一方観測者が聴く音波の振動数を $F$ とすると,時間 $\varDelta t_\mathrm{O}$ の間に観測者が受け取った音波の数は $F\varDelta t_\mathrm{O}$ である。音源から送り出された音波はすべて観測者に届くのであるから,2つの値は等しくなくてはならない。\[ \color{red}{観測者の受信波数 = 音源からの発信波数 } \\ \therefore F \varDelta t_\mathrm{O} = f\varDelta t \\ \therefore F = \bun{\varDelta t}{\varDelta t_\mathrm{O}}f \\ \quad = \bun{V}{V-v\cos\theta}f \cdots\cdots\maru{4} \]
これが,この場合に観測者が聴く音波の振動数ということになる。
ここで上式の分母中の $v\cos\theta$ は,音源の速度 $v$ のA→O方向成分,すなわち音源と観測者とを結ぶ方向(視線方向)の速度成分 $v_\perp $ にほかならない。そして $V-v\cos\theta$ は,音源に対する音源 → 観測者方向の相対音速ということになる。
このように,音源が斜め方向に運度する場合,音源の速度の視線方向成分によってドップラー効果が決まることが分かる。
*注.について - 公式の限界
上記では,$v\varDelta t \ll l$ の関係があるとして近似式を用い,振動数を導いた。
例として,音源速度を $v=30\mathrm{m/s}$ (時速108キロ)とし, $\varDelta t$ として音波の1周期分,たとえば $f = 500\mathrm{Hz}$ の音波とすれば, $\varDelta t=1/f=1/500=2\times 10^{-3}〔\mathrm{s}〕$ であるから,\[v\varDelta t=30\times 2\times 10^{-3} = 0.06\mathrm{m}\] 一方音源・観測点間距離として $l=1 \mathrm{m}$ とすれば,この場合十分に $v\varDelta t \ll l$ と言えるので,上の議論は概ね妥当と考えてよかろう。
ではつぎに, $v=70\mathrm{m/s}$ (時速252キロ),$f = 100\mathrm{Hz}$ の場合はどうだろうか。この場合,1周期間に音源が進む距離は,\[v\varDelta t = v \times 1/f=70\times 1/100 = 0.7\mathrm{m}\] となり,観測点までの距離が $l=1\mathrm{m}$ とすれば両者は同程度の値となってしまい,もはや近似を使う上記の議論では著しく正確性を欠く。
そもそもドップラー効果に関するこれまでの議論は,音源と観測者との間に十分な数の音波が存在するという前提の上に成り立っている。したがって $f = 500\mathrm{Hz}$ の音波であれば1波長は $\lambda=V/f=340/500=0.68\mathrm{m}$ であるから距離 $1\mathrm{m}$ の間には1波長程度の音波が含まれるが, $f = 100\mathrm{Hz}$ の音波であれば1波長は $\lambda=V/f=340/100=3.4\mathrm{m}$ であるから,距離 $1\mathrm{m}$ の間には1波長分の音波も含まれていないことになる。このような近距離においては,先に導いたドップラー効果の公式を適用することはできないのである。
ではどうすれば良いのか?
この場合は単に振動数の変化としてとらえることはできず,あくまでも音波の振動そのものの時間変化としてとらえていくしかないのである。
本シミュレーションでは,この考え方にもとづいて計算している。(本シミュレーションの場合 を参照)。
(2) 観測者が動く場合
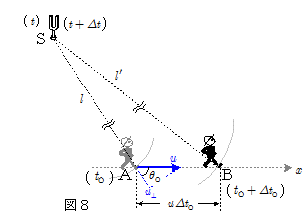
図8のように, $x$ 軸上を速度 $u$ で観測者が運動し,$x$ 軸の外に振動数 $f$ の音源Sが静止している。音速は $V\,\,(\, > \,u\,\,)$ とする。
音源から時刻 $t$ に発せられた音波が,時刻 $t_\mathrm{O}$ に$x$ 軸上の点Aで観測者に達し,また時刻 $t+\varDelta t$ に出た音波が,時刻 $t_\mathrm{O} +\varDelta t_\mathrm{O}$ に$x$ 軸上の点Bで観測者に達したとする。SA間,SB間の距離を $l$ , $l\,'$ とし,SAが $x$ 軸となす角を $\theta_\mathrm{O}$ とする。また $u \varDelta t_\mathrm{O} \ll l$ とし,$\bun{u \varDelta t_\mathrm{O}}{l}$ の2次の項は無視できるとすると,\[l\,' = \kon{l^2+(u\varDelta t_\mathrm{O})^2 - 2 u\varDelta t_\mathrm{O}\cdot l\cdot\cos(\pi - \theta_\mathrm{O})} \\ \quad \kinji l\bigg( 1 + 2\bun{u\varDelta t_\mathrm{O}}{l}\cdot \cos\theta_\mathrm{O} \bigg) ^{1/2} \\ \quad \kinji l + u\varDelta t_\mathrm{O}\cdot\cos\theta_\mathrm{O}\]ただし $|x| \ll 1$ のとき成り立つ近似式, $(1+x)^n \kinji 1+n\,x$ を適用した。よって時刻について,\[ \left \{ \begin{array}{rl}
& \kern-1em t_\mathrm{O} = t + \bun{l}{V} \\
& \kern-1em t_\mathrm{O} + \varDelta t_\mathrm{O} = t +\varDelta t+ \bun{l\,'}{V}
\end{array} \right . \\ \kern-1em \therefore \varDelta t_\mathrm{O} = \varDelta t + \bun{l\,'-l}{V} \\ \quad\quad \kinji \varDelta t + \bun{u\varDelta t_\mathrm{O}\cos\theta_\mathrm{O}}{V} \\ \therefore \bun{V-u\cos\theta_\mathrm{O}}{V}\varDelta t_\mathrm{O} = \varDelta t \] 発信波数=受信波数 より,\[ f\varDelta t = F \varDelta t_\mathrm{O} \\ \kern-1em \therefore F = \bun{\varDelta t}{\varDelta t_\mathrm{O}}f \\ \quad = \bun{V-u\cos\theta_\mathrm{O}}{V}f \] 上式中の $(V-u\cos\theta_\mathrm{O})$ は,観測者に対する視線方向の相対音速にあたる。
以上をまとめると,音源,観測者が斜め方向に運動している場合のドップラー効果は,それぞれの速度の視線方向(両者を結ぶ方向)成分を使って立式すればよいことが分かる。
◎時間間隔について に続く。