Thermoremanent magnetization of single-domain grains: Thermal activation theory

As shown in the previous page, it is necessary to apply a magnetic field \(H\) which is larger than the microcoercivity \(H_K\) to rotate the spontaneous magnetization \(M_s\) of a single-domain (SD) grain (when \(H\) is parallel to the easy axis). Using the formula of demagnetizing factors (Stacey & Banerjee 1974), \(H_K\) for a magnetite grain of spheroidal shape with elongation ratio 4/3 is, \[ H_K = (N_p - N_l)M_s = (11/30 - 4/15)\times 480\times 10^3 = 48\times 10^3\ \mathrm{A/m} \approx 0.06\ \mathrm{T}. \] \(H_K\) of 0.06 T (60 mT) is much larger than the geomagnetic field of ~0.00005 T (~50 μT), and yet volcanic rocks are able to record the paleodirections. This is partly due to small \(M_s\) and \(H_K\) at high temperatures, but more importantly due to thermal activations which help \(M_s\) to rotate by overcoming the energy barrier. The following sections introduce the theory of thermoremanent magnetization (TRM) of SD grains based on thermal activation, which was developed by Neel (1949). Notation of the formulas used here is mostly after Dunlop & Ozdemir (1997).

Thermal activation and relaxation time

Thermal activation at high temperatures causes \(M_s\), with a certain probability, to rotate over the energy barrier and align to the direction of \(H\). This is typical of a relaxation phenomenon which is described by Arrhenius' equation. In this equation, the reaction velocity \(K\) or the relaxation time \(\tau\) (inverse of \(K\)) is given by Boltzmann's factor, \begin{equation} K = \frac{1}{\tau} = A \exp\left(-\frac{E_a}{kT}\right), \label{eq01} \end{equation} where \(E_a\), \(T\), and \(k\) = 1.3807×10^-23 J/K are activation energy (energy barrier), temperature in Kelvin, and Boltzmann's constant, respectively. \(A\) is a constant specific to the reaction. In the case of magnetization of magnetite, \(A\) is 10⁸ ~ 10¹³ s^-1 and usually \(A\) = 10⁹ s^-1 is used.

Consider a mass of SD grains, each of which has a spontaneous magnetization \(M_s\). Suppose a weak magnetic field \(H\) is applied to these grains at a high temperature. As the relaxation time \(\tau\) is very short (say 1 s) at high temperatures, a certain amount of \(M_s\) will be aligned to \(H\) and a bulk magnetization will appear. If \(H\) is turned off, \(M_s\)'s will be randomized and the bulk magnetization will disappear almost instantly within 1 s or so. This state of magnetization is called superparamagnetism which is similar to paramagnetism but different in that each grain still has a spontaneous magnetization caused from ferromagnetism of the material. At this state of superparamagnetism, if the temperature is lowered while \(H\) is kept applied, the bulk magnetization becomes unchanged even if \(H\) is turned off. This is because \(\tau\) becomes extremely large at low temperatures due to its exponential relation to temperature. Setting \(A\) = 10⁹ s^-1 and \(E_a\) = const. in (1), an example of change of \(\tau\) on \(T\) is, \[ \tau = 1\ \mathrm{s\ at}\ T = 550°\mathrm{C}\ \longrightarrow\ \tau = 1.5768\times 10^{15}\ \mathrm{s\ (50\ Myr)\ at}\ T = 33°\mathrm{C}. \] Hence, magnetization induced at 550°C within 1 second becomes extremely stable at ~30°C for a long geological time. Actually this is a rather conservative estimation of \(\tau\) because \(E_a\) was supposed to be constant. As \(M_s\) and \(H_K\) becomes small at high temperatures, \(E_a\) also becomes small. Approximating temperature variation of both \(M_s\) and \(H_K\) being proportional to \(\sqrt{1 - T/T_C}\) where \(T_C\) is a Curie temperature, \(E_a\) ∝ \(M_s\)×\(H_k\) ∝ \((1-T/T_C)\). Taking this effect into consideration, change in \(\tau\) becomes, \[ \tau = 1\ \mathrm{s\ at}\ T = 550°\mathrm{C}\ \longrightarrow\ \tau = 1.5768\times 10^{17}\ \mathrm{s\ (5\ Gyr)\ at}\ T = 498°\mathrm{C}. \] Hence, with lowering of \(T\) by ~50°C, \(\tau\) becomes longer than the age of the earth! This phenomenon, magnetization turns from superparamagnetism to fixed, is called blocking of magnetization and the temperature at which magnetization becomes virtually fixed (blocked) is a blocking temperature (\(T_B\)).

↑ Top of this page

Thermal activation theory of TRM by Neel (1949)

Consider a spheroidal SD grain of volume \(V\) with a spontaneous magnetization \(M_s\). As described in the previous page, when a magnetic field \(H\) is applied along the easy axis, the total magnetic energy \(E\) is, \begin{equation} E = \mu_0 V M_s H_K\left(-(H/H_K)\cos\theta + {\tiny \frac{1}{2}}\sin^2\theta\right), \label{eq02} \end{equation}

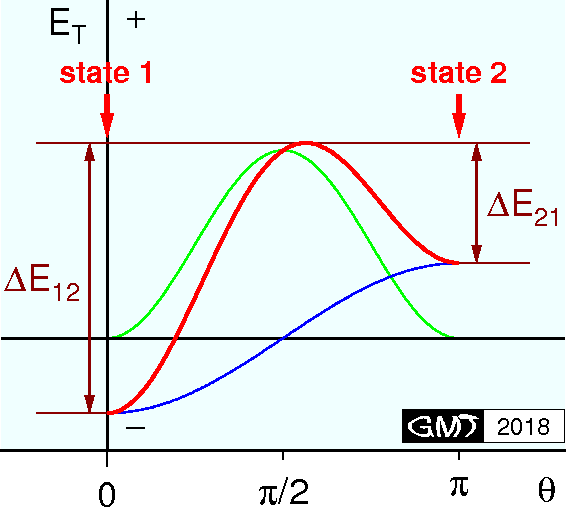
Now consider a mass of \(N\) such SD grains. Without any input of thermal energy, \(M_s\) of each grain stays at the initial position, state 1 or 2. When thermal activations are added, \(M_s\) of some grains will rotate by overcoming the energy barrier. As the energy barrier is lower for 2 \(\rightarrow\) 1 (π \(\rightarrow\) 0) than for 1 \(\rightarrow\) 2 (0 \(\rightarrow\) π), rotation 2 \(\rightarrow\) 1 will be more frequent than 1 \(\rightarrow\) 2. Eventually numbers of grains in state 1 (+\(M_s\)) exceed those of state 2 (-\(M_s\)) and the net magnetization of the \(N\) grains will be positive, aligned to \(H\).

Let \(n\) grains are in state 1 and \(N-n\) grains in state 2. Time derivative of \(n\) is expressed as, \begin{equation} \frac{dn}{dt} = K_{21}(N-n) - K_{12}n = \frac{N-n}{\tau_{21}} - \frac{n}{\tau_{12}}, \label{eq05} \end{equation} where \(K_{21}\) and \(K_{12}\) (\(\tau_{21}\) and \(\tau_{12}\)) are the reaction velocities (relaxation times) for the rotations of \(M_s\), 2 \(\rightarrow\) 1 and 1 \(\rightarrow\) 2, respectively. Introducing \(\tau\) as, \begin{equation} \frac{1}{\tau} = \frac{1}{\tau_{12}} + \frac{1}{\tau_{21}}, \label{eq06} \end{equation} equation (5) is written as, \[ \frac{dn}{dt} = \frac{1}{\tau_{21}}N - \frac{1}{\tau}n. \] Integrating this, \begin{gather*} \log\left(\frac{1}{\tau}n - \frac{1}{\tau_{21}}N\right) = -\frac{t}{\tau} + C, \\ n = C'\tau e^{-t/\tau} + \frac{\tau}{\tau_{21}}N, \end{gather*} where \(C\) and \(C'\) are constants of integration. As the numbers of grains to contribute to positive magnetization is \(2n-N\), \begin{eqnarray*} 2n-N & = & 2C'\tau e^{-t/\tau} + \left(\frac{2\tau}{\tau_{21}} -1\right)N, \\ & = & 2C'\tau e^{-t/\tau} + \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}N. \end{eqnarray*} Mean magnetization of \(N\) grains is, \begin{eqnarray*} M & = & \frac{2n-N}{N}M_s, \\ & = & \frac{2C'\tau}{N}M_s e^{-t/\tau} + \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s. \end{eqnarray*} Denoting the magnetizations at initial (\(t\) = 0) and equilibrium (\(t\) = ∞) states by \(M_0\) and \(M_{eq}\), respectively, \begin{eqnarray} M_0 & = & M(0) = \frac{2C'\tau}{N}M_s + \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s, \nonumber \\ M_{eq} & = & M(\infty) = \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s. \label{eq07} \end{eqnarray} Hence, \begin{equation} M = (M_0 - M_{eq})e^{-t/\tau} + M_{eq} = M_0 e^{-t/\tau} + M_{eq}(1 - e^{-t/\tau}). \label{eq08} \end{equation} Equation (8) suggests that if the relaxation time \(\tau\) is much larger than the observation time \(t\) (\(\tau \gg t\)) \(M\) stays at the initial state \(M_0\) while for the case of \(\tau\) much smaller than \(t\) (\(\tau \ll t\)) \(M\) reaches to \(M_{eq}\) which is given by (7).

Substituting the energy barriers \(\Delta E_{12}\) and \(\Delta E_{21}\) of (3) and (4) for the activation energy \(E_a\) in Arrhenius' equation (1), the equilibrium magnetization \(M_{eq}\) of (7) is, \begin{eqnarray} M_{eq} &=& \frac{\tau_{12}-\tau_{21}}{\tau_{12}+\tau_{21}}M_s, \nonumber \\ &=& \frac{\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H}{H_K}\right)^2\right] -\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H}{H_K}\right)^2\right]} {\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H}{H_K}\right)^2\right] +\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H}{H_K}\right)^2\right]}M_s, \nonumber \\ &=& \frac{\exp\left(\frac{\mu_0VM_sH}{kT}\right)-\exp\left(-\frac{\mu_0VM_sH}{kT}\right)} {\exp\left(\frac{\mu_0VM_sH}{kT}\right)+\exp\left(-\frac{\mu_0VM_sH}{kT}\right)}M_s, \nonumber \\ &=& M_s\tanh\left(\frac{\mu_0VM_sH}{kT}\right). \label{eq09} \end{eqnarray} This is the magnetization induced by \(H\) at a high temperature \(T\) in which \(\tau\) is much smaller than the observation time \(t\). Through subsequent cooling, the term of hyperbolic tangent in (9) is fixed at the blocking temperature \(T_B\) and the magnetization is frozen (blocked). With further cooling to the room temperature \(T_0\), only the \(M_s\) term increases to the value at \(T_0\). Hence, the magnetization at \(T_0\) is written as, \begin{equation} M(T_0) = M_s(T_0)\tanh\left(\frac{\mu_0VM_s(T_B)H}{kT_B}\right). \label{eq10} \end{equation} This is the TRM we observe at the room temperature. As the above theory was developed to the SD grains with a uniform orientation, Neel (1949) suggested to multiply \(1/3\) to (10) for those of random orientations. Although \(M\) is expressed by the Langevin function for randomly oriented grains (similar to the theory of paramagnetism), approximations for a small \(H\) become the same for both theories as below. \[ M(T_0)/M_s(T_0) \approx \frac{\mu_0 V M_s(T_B)}{3k T_B}H, \] which indicates that the intensity of TRM is proportional to the magnitude of the applied field when it is small. This is the basis for the method of determining the strength of the paleomagnetic field (paleointensity).

↑ Top of this page

Blocking temperature and cooling rate

Blocking temperature \(T_B\) is usually defined as the temperature at which the relaxation time \(\tau\) becomes equal to a characteristic time \(t\) of the cooling. The characteristic time \(t\) could be ~60 s for laboratory experiments or ~1 year for the cooling of a massive lava flow. Here, \(T_B\) is defined as the temperature at which the relaxation time \(\tau\) becomes equal to the time to cool 1°C, i.e. \(|dT/dt|^{-1}\). However, blocking does not occur at an exact temperature \(T_B\) but proceeds in a certain interval of temperature around \(T_B\). Hence, according to equation (8), the slower the cooling the blocking proceeds for longer time and the blocked magnetization is larger. The figure below shows simulation of blocking for magnetite SD grains when the temperature was decreased as a step function. At each step, the temperature was kept constant for a certain time and increase of \(M\) was calculated using (8) in which \(M\) was normalized by \(M_s\), i.e. only the term of hyperbolic tangent in (9) was considered. Simulation was started at 550°C supposing that the SD grains are in equilibrium with \(\tau\) = 1 s, i.e. in the state of superparamagnetism. In the figure red and blue lines show slow and fast cooling of 60 s and 10 s per 1°C, respectively (~9 hours and ~1.5 hours to cool to the room temperature, respectively). Green line like a step function is the equilibrium of \(M\) for the temperature of each step if infinite time is elapsed. The above defined \(T_B\)'s for slow and fast cooling are 544°C and 547°C, respectively, and the latter is almost the same as the temperature of 50% blocking. After further cooling of several degrees, 95% blocking was attained.

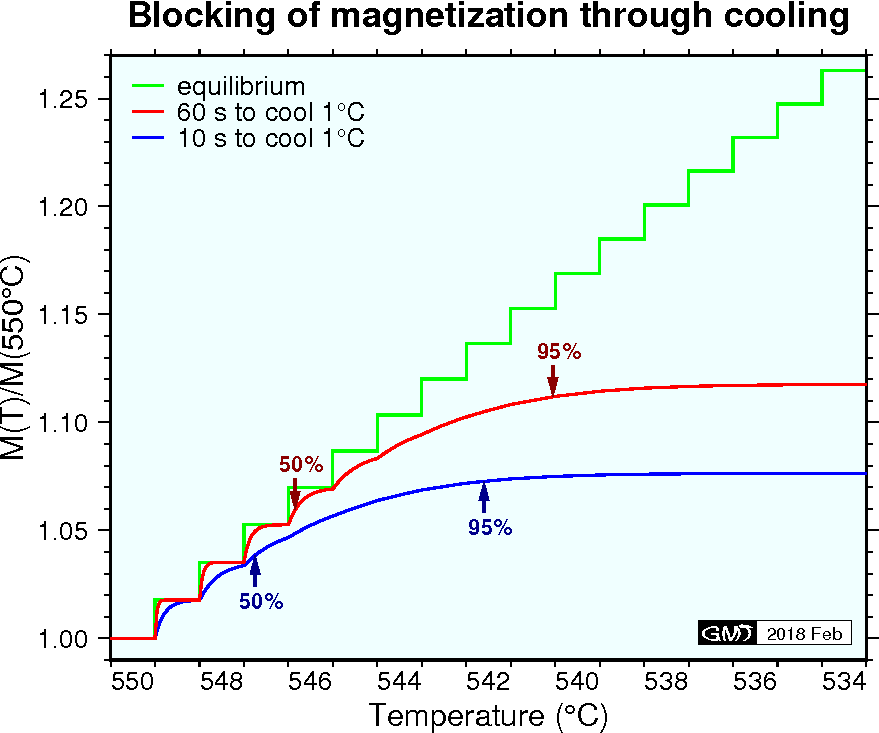
The results of simulation above might be different from the real blocking process in which cooling proceeds continuously. Nevertheless, it is known that blocking of TRM of volcanic rocks depends much on the cooling rate and the starting temperature. In the case of cooling from high temperatures just below \(T_C\), blocking completes within the temperature interval as narrow as a few degrees.

References:

• Dunlop, D. J., and O. Ozdemir, Rock Magnetism --- Fundamentals and frontiers ---, 573 pp., Cambridge University Press, Cambridge, 1997.
• Neel, L., Theorie du trainage magnetique des ferromagnetiques en grains fins avec applications aux terres cuites, Ann. Geophys., 5, 99--136, 1949.
• Stacey, F. D., and S. K. Banerjee, The Physical Principles of Rock Magnetism, 195 pp., Elsevier, New York, 1974.

↑ Top of this page   ← Previous page   → Next page