Magnetism of material: Magnetic moment of atoms
All material shows either of three different magnetic properties; diamagnetism, paramagnetism, and ferromagnetism. Diamagnetic material is repelled by a bar magnet although the force is so weak that it is detected only by using high sensitive magnetic instruments. Paramagnetic material is weakly attracted by a bar magnet although again magnetic instruments are necessary to detect the attractive force. Ferromagnetic material is easily attracted by a bar magnet. Differences of magnetic properties are manifestations of the magnetic state of the atoms which constitute the material. The followings are brief explanations of magnetism of atoms within the scheme of introductory physics although high-level quantum theory is necessary for accurate understanding.
Magnetic moment of atoms are caused by orbital and spin motions of electrons. In quantum mechanics, an electron's orbital angular momentum \({\bf L}\) is quantized and its magnitude is given by, \begin{equation} |{\bf L}| = \sqrt{l(l + 1)} \hbar \quad (l = 0, 1, \cdots, n-1) \label{eq01} \end{equation} where \(l\) is the orbital quantum number which takes zero or an integer, and \(\hbar\) = 1.0546×10-34 J s is Planck's constant. \(n\) is called the total quantum number which indicates that the electron is placed in the \(n\)th shell. When a magnetic field is applied to the atom, the component of \({\bf L}\) along the direction of the magnetic field (taken as \(z\)-direction) is also quantized as, \begin{equation} L_z = m_l \hbar \quad (m_l = -l, -l+1, \cdots, 0, \cdots, l-1, l), \label{eq02} \end{equation} where \(m_l\) is the magnetic quantum number. Spin angular momentum \({\bf S}\) of the electron is also quantized and its magnitude is given by, \begin{eqnarray} |{\bf S}| & = & \sqrt{s(s + 1)} \hbar \quad (s = \frac{1}{2}), \label{eq03} \\ & = & \frac{\sqrt{3}}{2} \hbar, \nonumber \end{eqnarray} and its component along the magnetic field is, \begin{eqnarray} S_z & = & m_s \hbar \quad (m_s = \pm\frac{1}{2}), \label{eq04} \\ & = & \pm\frac{1}{2} \hbar, \nonumber \end{eqnarray} where \(s\) and \(m_s\) are spin quantum number and spin magnetic quantum number, respectively.
Due to the quantized angular momenta, magnetic moment of an atom \({\bf m}\) is also quantized with the quantum of the Bohr magneton \(m_B\): \begin{equation} m_B = \frac{e \hbar}{2m_e} = 9.2732\times10^{-24}\ \mathrm{A\,m^2}, \label{eq05} \end{equation} where \(e\) and \(m_e\) are charge and mass of an electron, respectively. Using \(m_B\), magnitude and \(z\)-component of the orbital magnetic moment are given by, \begin{eqnarray} |{\bf m}^{\mathrm{ORB}}| & = & m_B \sqrt{l(l+1)}, \label{eq06} \\ m^{\mathrm{ORB}}_z & = & -m_B m_l. \label{eq07} \end{eqnarray} Magnitude and \(z\)-component of the spin magnetic moment are given by, \begin{eqnarray} |{\bf m}^{\mathrm{SPIN}}| & = & 2 m_B \sqrt{s(s+1)}, \label{eq08} \\ m^{\mathrm{SPIN}}_z & = & -2 m_B m_s. \label{eq09} \end{eqnarray} Note the different factor of 2 between the orbital and spin magnetic moments given by (6), (7) and (8), (9), respectively. For a single electron, \(|{\bf m}^{\mathrm{SPIN}}|\) and \(m^{\mathrm{SPIN}}_z\) are \(\sqrt{3}m_B\) and \(\mp m_B\), respectively.
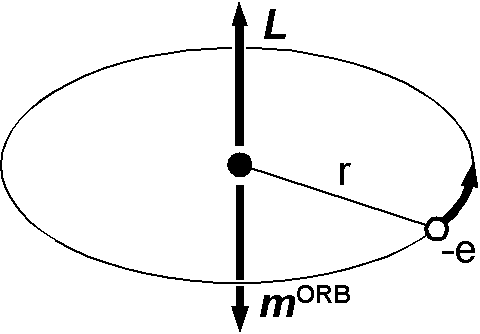
Bohr magneton (5) can be obtained by classical consideration using the Bohr model of an atom as shown in the figure. As the loop current multiplied by its area equals to a magnetic moment, \begin{eqnarray*} |{\bf m}^{\mathrm{ORB}}| & = & (\mathrm{current})\times(\mathrm{area}) \\ & = & (e \cdot \frac{\omega}{2\pi})(\pi r^2) = \frac{e \omega r^2}{2}, \end{eqnarray*} where \(\omega\) and \(r\) are electron's angular velocity and orbital radius, respectively. Angular momentum of the electron is given by, \[ |{\bf L}| = m_e \omega r^2. \] Eliminating \(\omega\) and \(r\) from these two equations and using (1), \[ |{\bf m}^{\mathrm{ORB}}| = \frac{e}{2m_e}|{\bf L}| = \frac{e\hbar}{2m_e}\sqrt{l(l+1)}. \]
Orbital and spin angular momenta are vectorially combined to a total angular moment \({\bf J} = {\bf L} + {\bf S}\). This applies to all electrons in the atom and each electron should have a different set of quantum numbers (Pauli's exclusion principle). Magnitude and \(z\)-component of the total magnetic moment \({\bf m}^{\mathrm{TOTAL}}\) are given by, \begin{eqnarray} |{\bf m}^{\mathrm{TOTAL}}| & = & g m_B \sqrt{J(J+1)}, \label{eq10} \\ m^{\mathrm{TOTAL}}_z & = & -g m_B M_J, \label{eq11} \end{eqnarray} with the Land\({\acute e}\) \(g\) factor and the combined quantum numbers \(J\) and \(M_J\). Values of \(g\), \(J\), and \(M_J\) can be calculated using a fairy complicated formula and value of \(g\) is usually between 1 (orbital contribution only) and 2 (spin contribution only).
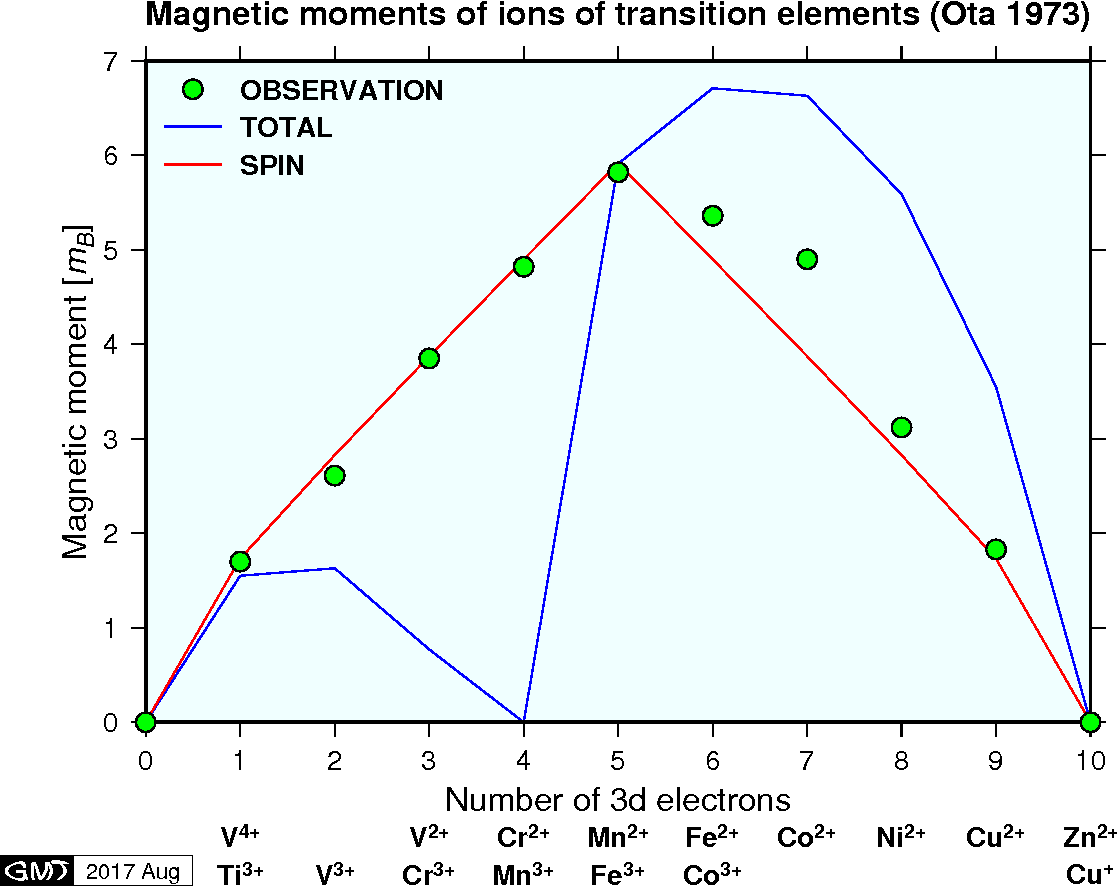
There is no orbital and spin angular momenta in the atoms in which the outermost shell is filled with electrons. Hence, magnetic moment does not arise in the rare gas atoms such as He and Ne. In some atoms \({\bf L}\) and \({\bf S}\) cancel out, leading to \({\bf J} = {\bf 0}\) and hence, zero magnetic moment. Most atoms show a magnetic moment a few times of \(m_B\). Some atoms, such as transition elements, show a larger magnetic moment more than several times of \(m_B\). In many atoms, contribution of orbital angular momentum disappears for various reasons, and hence spin is the main cause for atom's magnetic moment. The figure below shows experimentally determined magnetic moments for ions of transition elements (Ota, 1973). In the figure, the measured data show better agreement to the curve of SPIN (\(2m_B\sqrt{S(S+1)}\)) rather than TOTAL (\(g m_B\sqrt{J(J+1)}\)), indicating that contribution of \({\bf L}\) is almost zero.
In any case, most atom's magnetic moment are a few to several times of \(m_B\), which is so small compared to thermal perturbation. Hence, most atoms show either diamagnetism or paramagnetism. There should be a particular mechanism for elements to become ferromagnetic, which will be introduced in the next sections.
References:
- Ota, K., Basics of Magnetic Engineering I: Physics of Magnetism (in Japanese), 215 pp., Kyoritsu, Tokyo, 1973.