Magnetism of material: Diamagnetism and paramagnetism
Diamagnetism
Accurate description of diamagnetism needs difficult physics using theory of Larmor precession of the electron's orbit, but here elementary explanation is given. Diamagnetism is caused by electromagnetic induction between the loop current of an electron and an external magnetic field. When the magnetic field is newly added, the loop current is adjusted to cancel out the magnetic field, causing a magnetic moment with opposite direction to the magnetic field. Diamagnetism is the property of all atoms, but is easily masked when stronger paramagnetism emerges. Typical diamagnetic substance is quartz (SiO2) which is often used as a sample holder in magnetic measurements. We should be careful about the negative magnetism of the holder when the magnetism of the sample is small.
Paramagnetism
Paramagnetism emerges in the material which includes magnetic atoms but they have no interaction. Due to thermal fluctuation, magnetic moments of atoms are in random orientations and hence there is no bulk magnetic moment of the material. When a magnetic field is applied, magnetic moments of atoms tend to partially align to the field direction.
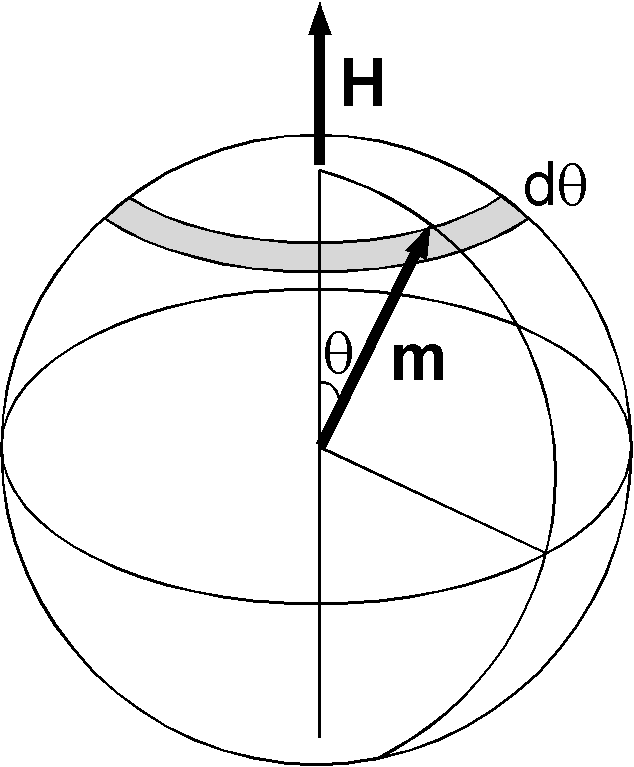
Figure shows the state in which the atom's magnetic moment \({\bf m}\) deflects from the applied field \({\bf H}\) by an angle \(\theta\). Magnetic potential energy \(U\) of the state is given by, \begin{equation} U = -\mu_0 m H \cos\theta. \label{eq01} \end{equation} According to statistical mechanics, the probability of the state to take place at temperature \(T\) K is given by Boltzmann's factor, \begin{equation} \exp\left(-\frac{U}{kT}\right) = \exp\left(\frac{\mu_0mH}{kT}\cos\theta\right), \label{eq02} \end{equation} where \(k\) = 1.3807×10-23 J/K is Boltzmann's constant. Probability for the magnetic moment to take the direction between \(\theta\) and \(\theta+d\theta\) is given by, \begin{equation} p(\theta)d\theta = \frac{2\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \sin\theta d\theta} {2\pi \int_0^\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \sin\theta d\theta}. \label{eq03} \end{equation} Magnetization \({\bf M}\) of the material induced by the applied field is caused by the component of \({\bf m}\) along the direction of \({\bf H}\). Hence, \(M\) is give by, \[ M = N m \overline{\cos\theta}, \] where \(N\) is the number of the atoms per unit volume. Using (3), \begin{eqnarray*} M & = & N m \int_0^\pi \cos\theta p(\theta) d\theta, \\ & = & N m \frac{\int_0^\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \cos\theta \sin\theta d\theta} {\int_0^\pi e^{\frac{\mu_0mH}{kT}\cos\theta} \sin\theta d\theta}. \end{eqnarray*} By substituting \(\frac{\mu_0mH}{kT} = \alpha\) and \(\cos\theta = x\), \[ M = N m \frac{\int_{-1}^1 e^{\alpha x} x dx}{\int_{-1}^1 e^{\alpha x} dx}. \] The denominator is easily obtained as, \[ \int_{-1}^1 e^{\alpha x} dx = \frac{e^\alpha - e^{-\alpha}}{\alpha}. \] Differentiating this result by \(\alpha\), the numerator is given by, \[ \int_{-1}^1 e^{\alpha x} x dx = \frac{e^\alpha + e^{-\alpha}}{\alpha} - \frac{e^\alpha - e^{-\alpha}}{\alpha^2}. \] Hence, \begin{eqnarray} M & = & N m \left( \frac{e^\alpha + e^{-\alpha}}{e^\alpha - e^{-\alpha}} - \frac{1}{\alpha} \right) \nonumber \\ & = & N m L(\alpha) \label{eq04} \end{eqnarray} where \(L(\alpha)\) is called the Langevin function; \begin{equation} L(\alpha) = \left( \coth\alpha - \frac{1}{\alpha} \right). \label{eq05} \end{equation} In general \(\alpha\) is quite small. For the magnetic moment of 1 Bohr magneton under a very strong field of 1×106 A/m (\(B\) of 1.26 T), \[ \alpha = \frac{\mu_0m_BH}{kT} = \frac{(4\pi\times10^{-7})(9.274\times10^{-24})(1\times10^6)} {(1.3807\times10^{-23})(300)} = 0.0028. \] For \(\alpha \ll 1\), the next approximation is applied; \begin{eqnarray*} \frac{e^\alpha + e^{-\alpha}}{e^\alpha - e^{-\alpha}} & = & \frac{1}{\alpha}\frac{1+\frac{1}{2}\alpha^2+\frac{1}{24}\alpha^4+\cdots} {1+\frac{1}{6}\alpha^2+\frac{1}{120}\alpha^4+\cdots} \\ & \approx & \frac{1}{\alpha}\left(1+\frac{1}{2}\alpha^2+\frac{1}{24}\alpha^4+\cdots\right) \left(1-\frac{1}{6}\alpha^2-\frac{1}{120}\alpha^4+\frac{1}{36}\alpha^4+\cdots\right) \\ & \approx & \frac{1}{\alpha}\left(1+\frac{1}{3}\alpha^2-\frac{1}{45}\alpha^4+\cdots\right). \end{eqnarray*} Hence, \begin{equation} L(\alpha) \approx \frac{1}{3} \alpha \quad (\alpha \ll 1). \label{eq06} \end{equation} Using (6), \(M\) of (4) is written as, \[ M = \frac{N m}{3} \alpha = \frac{\mu_0 N m^2 H}{3 k T}, \] and magnetic susceptibility \(\chi = M/H\) is given by, \begin{equation} \chi = \frac{\mu_0 N m^2}{3kT}. \label{eq07} \end{equation} This is the Curie's law of paramagnetism, which indicates that \(\chi\) is proportional to the inverse of temperature.
Although accurate derivation of \(\chi\) for paramagnetism should include quantum theory, (7) gives quite reasonable values. As an example, consider ilmenite (FeTiO3) which is paramagnetic at 300 K but antiferromagnetic (see next page) at very low temperatures. As molecular weight of ilmenite is 151.7 g, \[ N = 6.022\times10^{23}/151.7 = 3.970\times10^{21}\ \mathrm{g^{-1}} = 3.970\times10^{24}\ \mathrm{kg^{-1}}, \] and supposing the magnetic moment of Fe2+ ion as, \[ m = 5.4m_B = 5.4\times9.273\times10^{-24}\ \mathrm{Am^2}, \] (7) gives, \[ \chi_{mass} = 101\times10^{-8}\ \mathrm{m^3/kg}. \] This is in good agreement with the reported values of (100~113)×10-8 m3/kg (Dunlop & Ozdemir, 1997).
References:
- Dunlop, D. J., and O. Ozdemir, Rock Magnetism --- Fundamentals and frontiers ---, 573 pp., Cambridge University Press, Cambridge, 1997.