Miscellanies: core orientation by a sun compass; sunpmag
Rock samples for paleomagnetic measurements are usually collected by a portable drill and an orientation device with a sun compass. This is because using a drill and a sun compass is the most accurate and efficient method. This sampling scheme was first introduced to Japan by Dr. Masaru Kono (Prof. Emeritus of Tokyo Inst. Tech. and Okayama Univ.) in the 1960s. Dr. Kono also introduced a program to calculate the sun's azimuth. The program still works fine for 21st century with the error of less than ~0.1 degrees which is small enough for paleomagnetic purposes. Nevertheless, "sunpmag" introduces recent astronomical algorithm of Yallop and Hohenkerk (2007) in which the claimed error is ~0.6 minutes for the time span from 2000 BC to AD 2200. Although "sunpmag" is APPLICABLE ONLY to the orientation device supplied by Natsuhara Giken, the sub-function "sundir" which accurately followed the algorithm of Yallop and Hohenkerk (2007) will be useful to obtain the sun's azimuth and altitude in general.
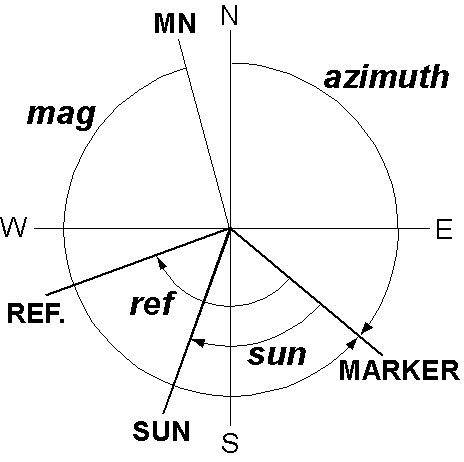The measurements system used in "sunpmag" is illustrated in the Right figure. We need to know the azimuth of the core marker which is measured clockwise from the true north. As it is difficult to know the true north in the field, we measure one to three angles: mag, sun, and ref. mag is the angle of the marker measured counterclockwise from the magnetic north. sun is the sun's direction (not the sun's shadow!) measured clockwise from the marker. ref is the direction of a reference also measured clockwise from the marker. If the magnetic declination at the site is available, it is included in the measurements data, but otherwise, the program calculates its IGRF or DGRF value corresponding to the date and site locality with altitude 0 km.
Given the sun's position on the celestial sphere at a certain time, the sun's azimuth and altitude observed at a certain location can be estimated with spherical trigonometry. Its basic principle is illustrated at the following sections.
Download and installation of the program
Spherical trigonometry
The followings are summary of main formulae of the spherical trigonometry, some of which are used to determine the sun's position in the sky.
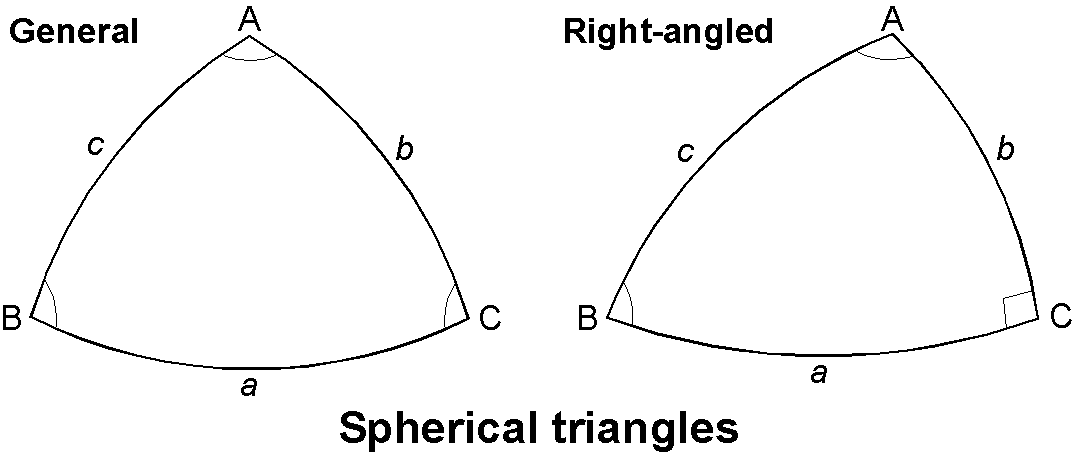
A spherical triangle is a figure formed by three arcs of great circles on the surface of a sphere. For an ordinary triangle (Left figure), \begin{equation} \frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} = \frac{\sin c}{\sin C}, \quad (\mathrm{sine\ rule}) \label{eq01} \end{equation} \begin{equation} \cos a = \cos b \cos c + \sin b \sin c \cos A, \quad (\mathrm{cosine\ rule}) \label{eq02} \end{equation} \begin{equation} \cos A = -\cos B \cos C + \sin B \sin C \cos a, \quad (\mathrm{cosine\ rule}) \label{eq03} \end{equation} \begin{equation} \sin a \cos B = \cos b \sin c - \sin b \cos c \cos A, \quad (\mathrm{sine\ cosine\ rule}) \label{eq04} \end{equation} \begin{equation} \cot a\sin b = \cos b\cos C + \sin C\cot A, \quad (\mathrm{cotangent\ rule}) \label{eq05} \end{equation} \begin{equation} \cot b\sin a = \cos a\cos C + \sin C\cot B, \quad (\mathrm{cotangent\ rule}) \label{eq06} \end{equation} In (2)~(6) variables can be permutated cyclically.
For a right-angled triangle with \(\angle\)C = 90° (Right figure), (1) becomes, \begin{equation} \frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} = \sin c. \label{eq07} \end{equation} In (4), permuting symbols \(a\)→\(b\), \(A\)→\(B\),\(\cdots\), and setting \(C\)=90°, the next formula is obtained. \begin{equation} \tan a = \tan c \cos B. \label{eq08} \end{equation}
It is noted that the sum of the three angles is larger than 180°. This is known from the next formula for the area \(S\) of the triangle, where \(r\) is the radius of the sphere, should be positive. \begin{equation} S = (A+B+C-\pi)r^2. \label{eq09} \end{equation}
Transformation from ecliptic coordinates to equatorial coordinates
The sun moves about 1° per day on the celestial sphere along a path which is called the ecliptic. As a first step to assign the sun's position on the celestial sphere, the ecliptic coordinates system is used. In the ecliptic coordinates, the sun's ecliptic latitude is always zero because it is on the ecliptic. The sun's ecliptic longitude is measured eastward from the vernal equinox along the ecliptic. In astronomy, \(\lambda\) is used to represent the ecliptic longitude, but here we use \(\phi_E\) because in paleomagnetism the former is used to show the geographical latitude. As a very crude approximation, the sun's ecliptic longitudes \(\phi_E\)s for the vernal equinox, the summer solstice, the autumnal equinox and the winter solstice are 0°, 90°, 180° and 270°, respectively. Of course, it is not such simple matter to estimate the sun's \(\phi_E\) accurate enough for navigation. This is because the sun's apparent movement is not constant due to oval shape of the earth's orbit and changes of its various elements together with the earth's rotation. The algorithm of Yallop and Hohenkerk (2007) takes care of all these effects except for the perturbations by planets, which can be excluded for the accuracy of 0.6 minutes.
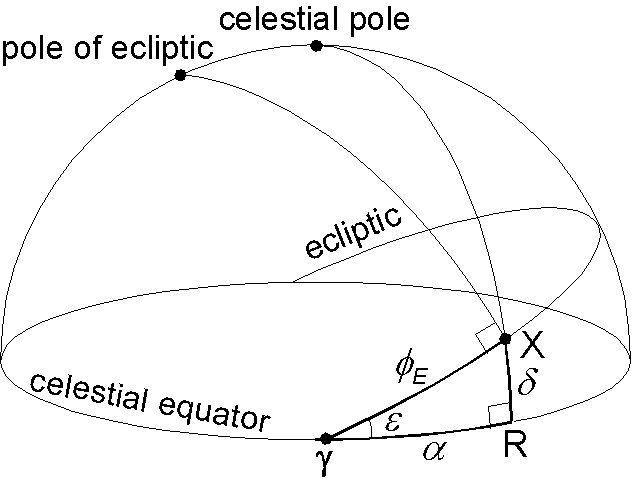
Next step is to convert the ecliptic coordinates of the sun to equatorial coordinates. In the equatorial coordinates, variable which corresponds to latitude is measured from the celestial equator with northward positive and is called declination \(\delta\) (do not confuse with the magnetic declination!). Another variable which corresponds to longitude is measured eastward from the vernal equinox and called right ascension \(\alpha\). The figure right illustrates the position of the sun around spring, in which X and \(\gamma\) are the sun and the vernal equinox. R is the point at which the great circle passing through the celestial pole and the sun intersects the celestial equator. \(\epsilon\) is the obliquity of the ecliptic which is about 23.5°. \(\epsilon\) varies with time and the program calculates it for a given time.
Given \(\phi_E\) and \(\epsilon\) for a specified time, \(\alpha\) and \(\delta\) are determined by applying the formulae of right-angled spherical triangle to \({\scriptsize \triangle}\)X\(\gamma\)R. Using (7) and (8), \begin{eqnarray} \sin \delta & = & \sin \phi_E \sin \epsilon, \label{eq10} \\ \tan \alpha & = & \tan \phi_E \cos \epsilon. \label{eq11} \end{eqnarray} For the right ascension \(\alpha\) obtained in (11), some adjustment of value is necessary depending which quadrant of the ecliptic the sun is positioned. However, using a function "atan2" of C language makes it simpler.
Transformation from equatorial coordinates to horizontal coordinates
Lastly, we calculate the sun's azimuth \(A\) and altitude \(h\) observed at a certain observation site. Here, following the convention in astronomy, the azimuth \(A\) is measured westward positive from the south. Left figure below illustrates the sun X observed at a site of the northern hemisphere middle latitude in summer afternoon. Right figure shows the situation at the same time for the southern hemisphere middle latitude with the same longitude (winter afternoon).
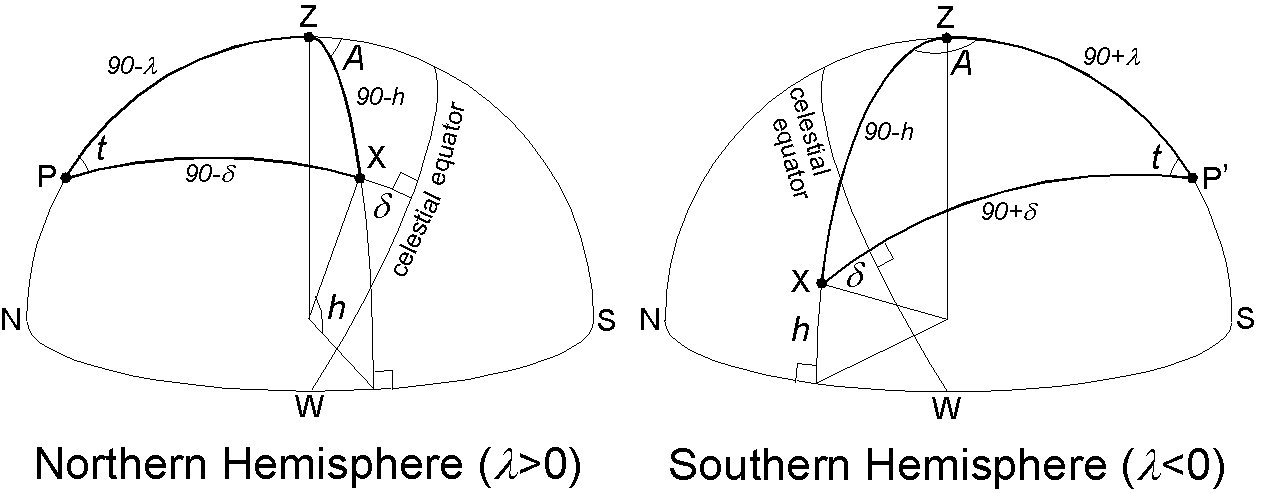
In the left figure, P and Z are the celestial north pole and the zenith, respectively. P' in the right figure is the celestial south pole. \(\lambda\) is the latitude of the observation site and \(\lambda\)>0 (\(\lambda\)<0) in the left (right) figure. The sun's declination \(\delta\) is the same positive value in both figures. \(t\) is the sun's local hour angle which is westward positive from the meridian. Although, in astronomy, \(t\) is usually represented by the unit of time in hours, here we use the unit of angle in degrees. The program calculates the sun's Greenwich hour angle \(t_G\) for the specified time using the right ascension \(\alpha\) together with some other orbital elements such as the obliquity of the ecliptic. The local hour angle \(t\) at the observation site is ahead from \(t_G\) by the site longitude \(\phi\) as, \[ t = t_G + \phi. \] In the left figure, let equation (2) be used to \({\scriptsize \triangle}\)PXZ, \begin{eqnarray} \cos(90-h) & = & \cos(90-\lambda)\cos(90-\delta) + \sin(90-\lambda)\sin(90-\delta)\cos t, \nonumber \\ \sin h & = & \sin\lambda\sin\delta + \cos\lambda\cos\delta\cos t. \label{eq12} \end{eqnarray} To obtain the azimuth \(A\), we use the next equation which is modified from the cotangent rule (6) after reverse cyclic permutation of symbols, \(a\)→\(c\), \(b\)→\(a\), \(B\)→\(A\), \(C\)→\(B\), \[ \tan A = \frac{\sin B}{\sin c \cot a - \cos c \cos B}. \] Applying this equation to \({\scriptsize \triangle}\)ZPX, \begin{eqnarray} \tan(180-A) & = & \frac{\sin t}{\sin(90-\lambda)\cot(90-\delta) - \cos(90-\lambda)\cos t}, \nonumber \\ \tan A & = & \frac{\sin t}{\sin\lambda\cos t - \cos\lambda\tan \delta}. \label{eq13} \end{eqnarray} It is easy to show that these two formulas to calculate the sun's azimuth and altitude hold to the case of right figure or other seasons and time. The value of \(A\) from (13) needs to be adjusted depending whether the triangle is acute-angled or not. However, use of "atan2" of C language makes this easier.
References:
- Yallop, B. D., and C. Y. Hohenkerk, Astronomical Algorithms for use with Micro-computers, NAO Technical Note No.67, HM Nautical Almanac Office, UK Hydrographic Office, 1989 (2007 updated). (→HM Nautical Almanac Office: Technical Notes)