 Miscellanies: circle fitting of X-Y data; pcirc
Miscellanies: circle fitting of X-Y data; pcirc
Program "pcirc" carries out circle fitting to 2-dimensional X-Y data (N≥3) by the method of Taubin (1991), and draws a PostScript figure of the fitted circle. This method seeks the circle parameter by minimizing the sum of the squares of "algebraic" distance \(r_i^2-R^2\) not the "geometric" distance \(r_i-R\), where \(r_i\) and \(R\) are the distance of a data point from the center and the radius of the circle, respectively. Although the algebraic fits are less accurate than the geometric fits, they are practical due to their fast calculation speed. For introduction to the theory, → see this page. The C program code used in "pcirc" is adapted from the C++ routines of Chernov (2012).
Example of circle fit
The following example uses a test data file, test.d, which includes four data points; (1.1, 0), (0, 0.9), (-1.1, 0), (0, -0.9). Circle fitting to these four data points is carried out by typing as
pcirc test.d -c -lwhere "-C" and "-L" are options to plot a circle center and list out the input data to the display, respectively. Results of circle fitting are shown as,
Circle fitting of test.d
PS file: test.ps
N X0 Y0 R k SSE
4 0.000 0.000 1.005 0.000 0.04010
Input data:
i X Y Error
1 1.100 0.000 0.09501
2 0.000 0.9000 -0.1050
3 -1.100 0.000 0.09501
4 0.000 -0.9000 -0.1050
where "(X0,Y0)" and "R" are the center and the radius of the fitted circle, respectively. "k" and "SSE" are a measure of the curvature and sum of the squares of the "Error" which is \(r_i-R\), respectively. They are used to evaluate the paleointensity data, and hence can be ignored for general data (see "MEMOS_PMAGM302.pdf" contained in "pmagm302.tar.gz"). Figure below is the output PS file "test.ps".
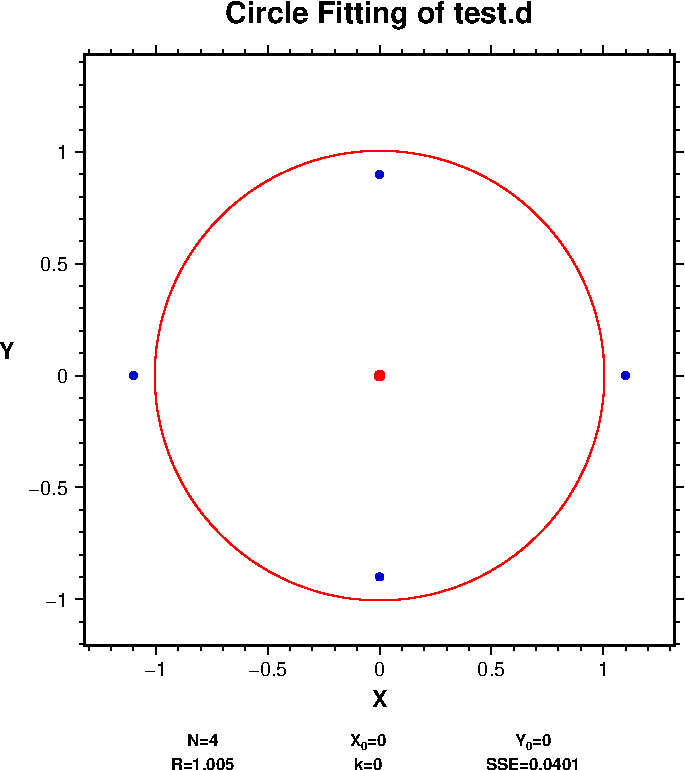
Note that the radius R is slightly larger than the optimal value of 1. As mentioned above, the algebraic methods are less accurate than the geometric methods because the former minimize the sum of the squares of "\(r_i^2 - R^2\)", not that of "\(r_i - R\)". Nevertheless, the former algorithm is simpler and fast in calculation speed, and hence widely used.
Download and installation of the program
References:
- Chernov, N, Fitting ellipses, circles, and lines by least squares, 2012. (URL: →http://people.cas.uab.edu/~mosya/cl/ index.html)
- Taubin, G., Estimation of planar curves, surfaces and nonplanar space curves defined by implicit equations, with applications to edge and range image segmentation, IEEE Trans. Pattern Analysis Machine Intelligence, 13, 1115-1138, 1991.