Miscellanies: main field elements
Program "igrf" provides interactive calculations of geomagnetic main field elements at a certain site and date for the time span AD 1900~2025. It is possible to select either geodetic or geocentric coordinate system and assign the site altitude or a radius from the earth's center. Gauss coefficients are taken from IGRF-13 (IAGA Working Group V-MOD, 2020) and inclusion of higher terms is limited to n=m=10. Although IGRF-13 provides coefficients up to n=m=13 for the time span from AD 2000 onward, the elements values given by "igrf" should be accurate enough for paleomagnetic purposes. Differences from those for n=m=13 are 0.2-0.4° in field direction, and 0.2-0.4% in total force excluding the regions near to the magnetic poles.
Interactive calculation
In default, latitude and longitude of the site location is in geographic (geodetic) system and input format is decimal for both site and date. The following is an example when typing just "igrf" and continued by typing Return.
igrf Main field calculation from IGRF-13 with n=m=10 Rtn (Enter) to continue, U for usage, H for help message, Q to quit. ** Geodetic system adopted. ** Decimal year? (Q - quit) 2019.3 Altitude in km? (-10 ~ 500 km) (Rtn - 0 km, Q - quit) 0.2 Decimal Lat, Lon? (Q - quit) 64.7 -26.4 Year altitude 2019.300 0.2 Latitude Longitude 64.70 -26.40 X Y Z F I D 12220 -3473 51309 52858 76.09 -15.87 Decimal Lat, Lon? (Q - quit)
With -C option calculation is made in geocentric system with a certain radius from the earth's center. Inputs by "year, month, day" and "degrees, minutes" are possible by -Y and -D options, respectively.
Input from a file
With -F option, "igrf" reads the sites and dates from a file and outputs the results to the display. Both decimal and other formats of the input data are accepted but the coordinate system is only geodetic. The following is an example.
igrf -f t-igrf.d > result.txt
Contents of "result.txt" are as the following.
** IGRF elements from t-igrf.d **
** Geodetic system adopted. **
Year Mo Dy altitude
2020 5 15 0.2
Lat-d Lat-m Lon-d Lon-m
33 24 -133 36
X Y Z F I D
24192 5678 35552 43376 55.05 13.21
...
... the rest is omitted ...
...
Download and installation of the program
Summary of formulas
Let \(X\), \(Y\), and \(Z\) be the northward, eastward, and vertical down components, respectively, of the geomagnetic field \({\bf B}\) observed at (\(r,\theta,\phi\)). Using the Gauss coefficients \(g_n^m\) and \(h_n^m\), the three components are calculated by the following formulas in which \(P_n^m(\cos\theta)\) is the quasi-normalized Schmidt function (associated Legendre polynomials). \begin{eqnarray*} X & = & \sum_{n=1}^\infty\left(\frac{a}{r}\right)^{n+2}\sum_{m=0}^n(g_n^m\cos m\phi + h_n^m\sin m\phi)\frac{dP_n^m(\cos\theta)}{d\theta}, \\ Y & = & \sum_{n=1}^\infty\left(\frac{a}{r}\right)^{n+2}\sum_{m=0}^n(g_n^m\sin m\phi - h_n^m\cos m\phi)\frac{m P_n^m(\cos\theta)}{\sin\theta}, \\ Z & = & -\sum_{n=1}^\infty(n+1)\left(\frac{a}{r}\right)^{n+2}\sum_{m=0}^n(g_n^m\cos m\phi + h_n^m\sin m\phi)P_n^m(\cos\theta). \end{eqnarray*}
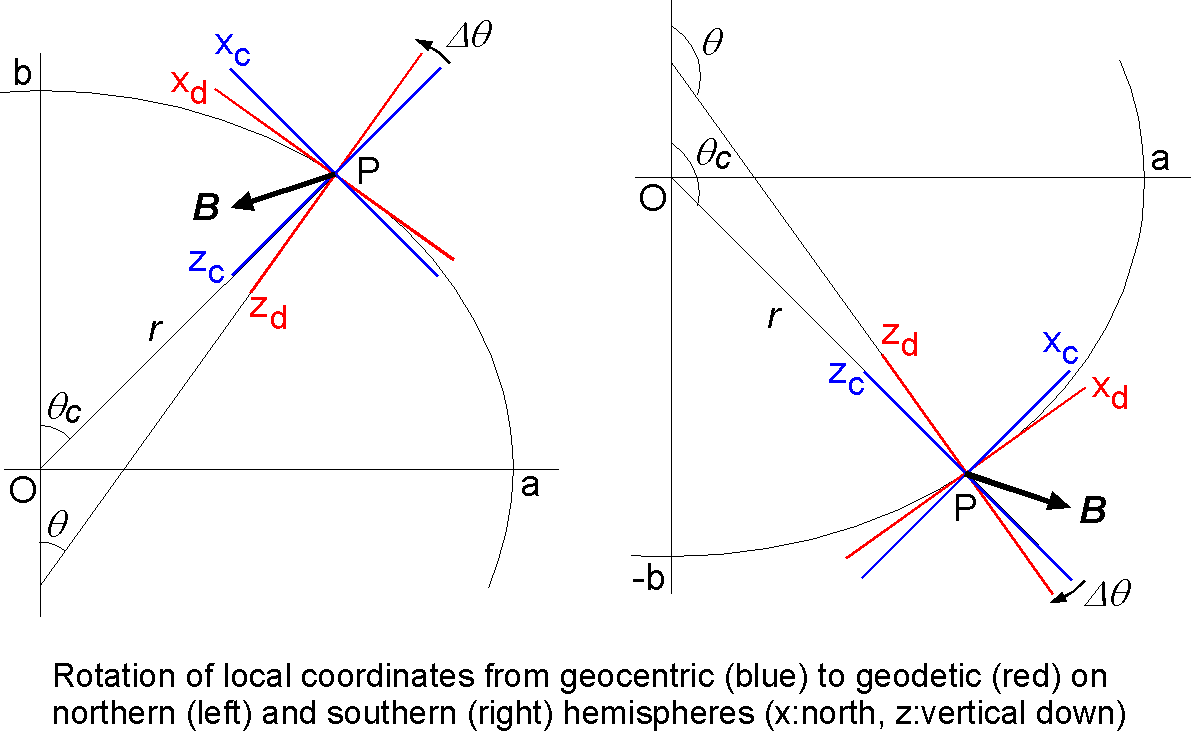
Above formulas hold only in geocentric coordinate system while geographic (geodetic) coordinate system is used in maps and navigation. Hence, we first transfer geodetic colatitude \(\theta\) to geocentric one \(\theta_c\) and estimate the radius \(r\) from the earth's center by using transfer equations in geodesy (for details, see "MEMOS_PMAGT401.pdf" contained in "pmagt401.tar.gz"). Then field elements (\(X_c,Y_c,Z_c\)) in geocentric system is calculated by using the above formulas. Lastly the field elements in geocentric system is transferred to those in geodetic system (\(X,Y,Z\)) by the following equation in which \(\Delta\theta\) is the signed difference angle between the two local coordinate systems on the observation point P. \[ \left(\begin{array}{c} X \\ Y \\ Z \end{array}\right) = \left(\begin{array}{ccc} \cos\Delta\theta & 0 & \sin\Delta\theta \\ 0 & 1 & 0 \\ -\sin\Delta\theta & 0 & \cos\Delta\theta \end{array}\right) \left(\begin{array}{c} X_c \\ Y_c \\ Z_c \end{array}\right) \]
Figures below show the relations of the field vector \({\bf B}\) observed at P and the rotation of the local coordinate systems for northern (Left) and southern (Right) hemispheres.
References:
- IAGA Working Group V-MOD, International Geomagnetic Reference Field: IGRF-13 is released, 2020. (URL: https://www.ngdc.noaa.gov/IAGA/vmod/igrf.html)