定義：確率変数Xは「連続型」、

定義：確率変数X (もしくはP^X) の「確率密度関数(Probibility Density Function)」

　　f_x: R¹→[0,∞]が存在して、

　　　　　　　　　　…（１）

　　　　　　　　for ∀x∈R¹ 　

　　X ( P ^x )を連続型確率変数

　　Fを絶対連続な分布関数(→柳川p16)といい、

　　f(・)をX ( P ^x )の確率密度関数(pdf)という。

　　　　(1)の右辺はルベーク式積分によって定義されるのだが、

　　　　　　　f_xの広義積分

　　　　　（野田・宮岡『数理統計学の基礎』p.22）

1. f_x(x)≧0　for ∀x∈R¹　

　　(証明)

　　(i)確率密度関数の定義と、分布関数の性質から。(柳川p.16)

　　(ii)

　　　　　　　　　　　　∵確率密度関数の定義　

　　　　　　　　＝１　　　　　　　　∵分布関数の性質　　　

　　(i) f_x の連続点xで、

　　　　　F ' _X(x)=f_X(x) 　

　　(ii)

　　　{ω∈Ω| a＜X(ω)≦b}は{ a＜X≦b }

　　　{ω∈Ω| X (ω)∈B}は{ X∈B }

　　　　　　　野田・宮岡『数理統計学の基礎』p15.

　　(証明)

　　(i)　微積分学の基本定理から。　　（柳川p16）

　　(ii)　

　　　　P (a<X≦b)= P ({ω∈Ω| a＜X(ω)≦b})=F_X(b)−F_X(a)　

　　　　　　　　　　　　　∵　　定理：　P ( {ω∈Ω| a＜X(ω)≦b } )=F_x(b)−F_x (a)　

　　　　　　　　　　　　　　　　　　　∵a<b

例：指数分布 (exponential distribution)

　　　　　　　　鈴木・山田『数理統計学―基礎から学ぶデータ解析―（第二版）』pp. 112-113。

　　　f_x(x)= 0 　　　(x＜0)

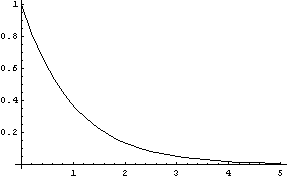
　・定理：指数分布の「無記憶性(鈴木・山田p.112)」・「記憶喪失性(『統計数学』pp.88-89)」

　　P ( X > x+h | X > x ) = P (X≧h)

　　　　for ∀x, h＞0

　　　{ω∈Ω| a＜X(ω)≦b}は{ a＜X≦b }

　　　{ω∈Ω| X (ω)∈B}は{ X∈B }

　　　　　　　野田・宮岡『数理統計学の基礎』p15.

　　(解釈)

　　(証明)　　

　　左辺：P ( X > x+h | X > x )＝P ( {ω∈Ω| X(ω) > x+h } | {ω∈Ω| X(ω) > x } )　　(略記法から戻す)

　　　　　　　　　＝P ( {ω∈Ω| X(ω) > x+h }∩{ω∈Ω| X(ω) > x } ) ／P ( {ω∈Ω| X(ω) > x })　　

　　　　　　　　　　　　　　　　　　　　　　　　　∵条件付確率の定義　P(A|B) ≡ P (A∩B) / P(B)　

　　　　　　　　　＝P ( {ω∈Ω| X(ω) > x+h } ) ／P ({ω∈Ω| X(ω) > x } )　　

　　　　　　　　　＝[1−P ( {ω∈Ω| X(ω) > x+h } ^C ) ] ／ [ P ({ω∈Ω| X(ω) > x } ^C ) ]　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　∵余事象の確率：P(A^c)=1−P(A)

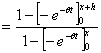
　　　　　　　　　＝[ 1−P ( {ω∈Ω| X(ω) ≦ x+h } ) ] ／ [ 1−P ({ω∈Ω| X(ω) ≦ x } ) ]　　　

　　　　　　　　　＝[ 1−F_X ( x+h ) ]／[ 1−F_X ( x ) ]　　　　　　　　　　　　　　∵分布関数の定義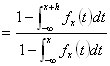　

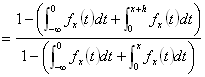
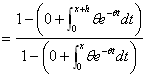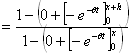
　　　　　　　　　　　　　　　　　　　　　　　　　　　　∵確率密度関数の定義　

　　　　　　　　　　　　　　　∵指数分布の定義　　　　

　　右辺：P (X≧h) ＝P ( {ω∈Ω| X(ω) ≧ h } )　　(略記法から戻す)

　　　　　　　　　　= P ( {ω∈Ω| X(ω) ＞ h } ∪ {ω∈Ω| X(ω) ＝ h })　　

　　　　　　　　　　= P ( {ω∈Ω| X(ω) ＞ h } )＋P ( {ω∈Ω| X(ω) ＝ h } )　

　　　　　　　　　　　　　　　　　∵排反なので確率の公理(P3)より　　　　　

　　　　　　　　　　= P ( {ω∈Ω| X(ω) ＞ h } )＋P ( {ω∈Ω| X(ω) ＝ h } )　　　

　　　　　　　　　　＝ 1−P ( {ω∈Ω| X(ω) > h } ^C ) ＋P ( {ω∈Ω| X(ω) ＝ h } )　　　

　　　　　　　　　　　　　　　　　　　　　　　　∵余事象の確率：P(A^c)=1−P(A)

　　　　　　　　　　＝ 1−P ( {ω∈Ω| X(ω) ≦ h } ) ＋P ( {ω∈Ω| X(ω) ＝ h } )　　　

　　　　　　　　　　＝ 1−F_X ( h )＋0　　　　　　　　　　　　　　　∵分布関数の定義　

　　　　　　　　　　　　　　　　　　　　　　　　　∵確率密度関数の定義　

　　∴P ( X > x+h | X > x )＝P (X≧h) 　　

（reference）

文献1.『岩波数学辞典（第三版）』項目47C(p.128).

文献2. 佐藤坦『はじめての確率論　測度から確率へ』共立出版、1994、p.28;101.

文献3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、pp.27-26; 112-113。

文献4. 柳川堯『統計数学』近代科学社、1990年,pp.16-17; 18-19.

文献5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、pp.22-24 。