条件付確率(conditional probability)

　　：確率空間(probability space)

　　A,B∈ , P(B)>0とするとき、

　　P(A|B)を以下のように定義する。

　　　　　P(A|B) ≡ P (A∩B) / P(B)
　　　(これが確率であるかどうかは、以下で検討)

　　P(・|B)、B∈ ,P(B)>0は(Ω,)上の確率、

　　(Ω, A, P(・|B) ), B∈A ,P(B)>0は確率空間(probability space)

　　確率の定義(P1)-(P3)をP(・|B)が満たすことを示せばよい。

　　(P1)　0≦P(A|B)≦1 ∀A∈A

　　　　・A∩B⊂B。

　　　　　　∴　P(A∩B) ≦P(B)　　∵確率の単調性　　

　　　　確率の定義より、確率は少なくとも正なので、

　　　　　0≦P(A∩B) ≦P(B)

　　　　両辺をP(B)>0で割って、

　　　　　0≦P(A∩B)／P(B)≦1

　　　　∴　0≦P(A|B)≦1
　　　　→矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p.151.

　　(P2)　P(B|B)=1

　　　　P(B|B)=P(B∩B)/P(B)=P(B)/P(B)=1.
　　　　→矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p.151.

　　(P3) A₁,A₂,…∈A , A_i∩A_j=φ (i≠j)

　　[前提]

　　　A₁,A₂,…∈A

　　　A_i∩A_j=φ (i≠j) [A_iとA_jは排反](＊)

　　　B∈A ,P(B)>0

　　　(＊)より、

　　　(A_i∩B)∩(A_j∩B)=φ(i≠j) [(A_i∩B)と(A_j∩B)は排反](＊＊)

　　　　∵定義P(A|B)

　　　　　　　∵集合の分配則

　　　　　　　　　　　P(A|B)が確率であるかどうかは

　　　　　　　　　　P(A)は確率として定義済み。

　　　　　　　　　　これに確率の定義(P3)を適用できる。

　　　　　　　　　　　(＊＊) (A_i∩B)∩(A_j∩B)=φ(i≠j)より、

　　　　　　　∵定義P(A|B)

　　　→野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、pp.9-10.

　　(Ω, A, P )：確率空間(probability space)

　　A,B∈A ,P(B)>0とする。

　定義：事象Bが与えられたときの事象Aの条件付確率

　　　(conditional probability of the event A given the event B)

　　P(A|B) ≡ P (A∩B) / P(B)は上記の定理より(Ω, A)上の確率であり、

　　これを、事象Bが与えられたときの事象Aの条件付確率

　　　(conditional probability of the event A given the event B)

　定義：事象Bが与えられたときの条件付確率(測度)

　　　(conditional probability given the event B)

　　P(・|B) は上記の定理より(Ω, A)上の確率であり、

　　これを、Bが与えられたときの「条件付確率(測度)」

　　　(conditional probability given the event B)

　　P (A∩B) = P(B)P(A|B)　　∵P(A|B)の定義を移項しただけ。

　A‖B　：事象AとBは互いに独立である。

　　⇔P(A|B)=P(A)⇔P(B|A)=P(B)⇔P(A∩B)=P(A)P(B)

　　　P(A)≠0,P(B)≠0

　(proof)

　　P(A|B)=P(A)⇔P(B|A)=P(B)⇔P(A∩B)=P(A)P(B)となることの証明

　　P(A|B)=P(A)　

　　これは左辺P(A|B)の定義から以下と同じ。

　　P(A∩B)/P(B)=P(A)

　　これは、これの両辺にP(B)をかけた以下と同じ。

　　P(A∩B)=P(A)P(B)

　　これは、P(A)でこの両辺を割った以下とも同じ。

　　P(A∩B)/P(A)=P(B)

　　これはP(B|A)の定義から以下と同じ。

　　P(B|A)=P(B)

　(注)

　　P(A∩B)=P(A)P(B)を事象の独立の定義とするものと、

　　P(A|B)=P(A)を独立の定義として、P(A∩B)=P(A)P(B)を独立の必要十分条件を与える定理とするものがある。

　　前者では、P(A)=0,P(B)=0を排除せず、P(N)=0を満たす事象Nは任意の事象に対して常に独立であるという定理が提示される。

　　後者では、そもそも、P(A)=0のときP(B|A)が定義されていない、P(B)=0のときP(A|B)が定義されていない、ということから、これらのケースが排除されたかたちで、独立が定義されている。

　事象AとBが独立であれば、AとB^c、A^cとB、A^cとB^cとは独立である。

　(proof)

　　　「事象AとBが独立である」とは、すなわち、

　　　P(A∩B)=P(A)・P(B)　　−(1)

　　　事象AとBが独立であれば、(1)が成立する。

　　　P(A)・P(B^c)=P(A)・(1-P(B))　∵余事象の確率

　　　　　　　　 =P(A)−P(A)・P(B)

　　　　　　　　 =P(A)−P(A∩B)　　　∵ (1)

　　　　　　　　 =P(A∩B^c) 　　　∵ ベン図を描けばわかる

　　　　　∴A‖B^c　∵ 独立の定義　　

　　　P(A^c)・P(B)=(1−P(A))・P(B)　∵余事象の確率

　　　　　　　　 =P(B)−P(A)・P(B)

　　　　　　　　 =P(B)−P(A∩B)　　　∵ (1)

　　　　　　　　 =P(B∩A^c) 　　　∵ ベン図を描けばわかる

　　　　　∴A^c‖B　∵ 独立の定義

　　　P(A^c)・P(B^c)=(1−P(A))・(1−P(B))　∵余事象の確率

　　　　　　　　 =1−P(A)−P(B)＋P(A)・P(B)

　　　　　　　　 =1−P(A)−P(B)＋P(A∩B)　　　∵ (1)

　　　　　　　　 =1−{ P(A)＋P(B)−P(A∩B)}

　　　　　　　　 =1-P(A∪B) 　　　∵確率の加法則

　　　　　　　　 =P(A^c∩B^c)

　　　　　∴A^c‖B^c　∵ 独立の定義

　事象A₁,…..,A_nから、どの二つの事象をとっても独立であるとき、

　事象A₁,…..,A_nは、対独立(pairwise independent)と呼ばれる。

　　→野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.13

　　　（例）三個の事象A,B,Cが、　A‖B、　B‖C、　C‖A。

　n個の事象{ A₁,…..,A_n }について、

　任意にとられた1≦m≦n,　1≦i₁＜i₂＜…＜i_m≦nに対し、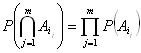

　が成り立つとき、事象系{ A₁,…..,A_n }は独立であるとよばれる。

　　　（例）三個の事象A,B,Cが独立であるとは、

　　　　　　P(A∩B)=P(A)P(B)　（すなわちA‖B）

　　　　　　P(A∩C)=P(A)P(C)　（すなわちB‖C）

　　　　　　P(B∩C)=P(B)P(C)　（すなわちC‖A）

　　　　　　　　（以上三行、すなわちA,B,Cは対独立）

　　　　　　P(A∩B∩C)=P(A)P(B)P(C)

　　・A‖B、B‖C、C‖Aであっても、

　　　　P(A∩B∩C)=P(A)P(B)P(C)は必ずしも成立しない。

　　・P(A∩B∩C)=P(A)P(B)P(C) であっても、

　　　　A‖B、B‖C、C‖Aは必ずしも成立しない。

　　→柳川堯『統計数学』近代科学社、1990, p.9.

文献3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、pp. 12-15。

文献4. 矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p.150-155.　詳しくはないが、P(・｜B)も確率測度であることを示す証明がついている。

文献5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.9-13 。　わかりやすい。厳密であると同時に、わかりやすい解釈がつけられている。

文献6. 柳川堯『統計数学』近代科学社、1990, pp.6-9.　簡潔。複数の事象の間の独立については詳しく論じられている。