確率変数
(random variable)ゆるい!最小のσ集合族⇒ボレル集合族⇒確率変数の定義のラインを佐藤著で強化しないとだめ。
おおよその意味:
R 1およびR nのσ加法族。(引用集)
鈴木・山田『
数理統計学(第二版)』p.21.Rnのボレル集合族
「
R nのすべての区間を含む最小のσ加法族」柳川『
統計数学』p.12.Rのボレル集合族
「
R上の区間(a,b]全体からなる集合を含む最小のσ加法族が存在する。 この集合族をボレル集合族といい、![]() であらわす。」
であらわす。」
野田・宮岡『
数理統計学の基礎』pp.3-4「区間」:
「
n次元ユークリッド空間R n = {( x1, x2, …,xn )|xi∈ R (i=1,2,…n)}において、−∞≦
ai≦bi≦∞(i=1,2,…n)について、I=(a1, b1]×…×(a n, bn]={( x1, x2, …,xn )| a i< xi ≦bi (i=1,2,…n)}
なるかたちの集合
IをR nにおける区間(interval)とよぶ。ただし、
bi=∞の場合には、上述の表現における不等式a i< xi≦bi
は
a i< xI<∞
とおきかえることを規約する。」
「
In」:このような区間の全体を
Inと記す。「ボレル集合族
(Borel Family of sets)/ボレル集合体(Borel field)/ボレル代数(Borel algebra)」:「
(1.1.4)によって、R nにおいて、Inを含む最小のσ加法族
が存在するが、これをボレル集合族、ボレル集合体、ボレル代数などとい
![]()
によってあらわす。
「ボレル集合
(Borel set)」: ![]() に属す集合はボレル集合
に属す集合はボレル集合
開区間、閉区間、
n次元球、1点のみからなる集合、可算個の点からなる集合などはボレル集合である。
※
最小のσ加法族というときの「最小」って??佐藤『
はじめての確率論 測度から確率へ』pp.11-15.定義:ボレル集合体
(p.13)「
E=(E,d)を距離空間、OをEの開部分集合全体からなる集合族とする。このとき、
Oから生成されるE上のσ集合体B(E)≡σ(O)をE上のボレル集合体、
Eの部分集合でB(E)に属するものをEのボレル集合という。」
補題
2.3(pp.13-14)「
Eを距離空間とする。このとき、
Eの開部分集合、閉部分集合、コンパクト部分集合、可算集合、有限集合は
すべて
Eのボレル部分集合である。」証明:
定義:d次元ボレル集合体
(pp.14-15)「特に重要なのは
Eがd次元ユークリッド空間Rdの場合である。上の
Rd上のボレル集合体B(Rd)を簡単のためBdと書き、d次元ボレル集合体、また
Bdに属するRdの部分集合をd次元ボレル集合という」補題
2.4 (p.14)Jd≡{ ( a1, b1 ]×…×( ad , bd ]⊂Rd:−∞≦ak≦bk≦∞, k=1,2,…d }
と定義すると
BdはJdから生成されるRd上のσ集合体である。すなわち、Bd=σ[ Jd ]
ただし、上の定義で
(a,+∞]は(a,+∞)をあらわすものとする。証明:
・
Ω上の実数値関数 X(ω) が
X−1 (B)∈
を満たす。
⇔
Xは・
Ω上の実数値関数 X(ω) が
X−1 (B)∈
を満たす。
⇔
Xは 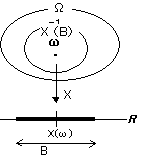
※ 略記法
{ω∈Ω
| a<X(ω)≦b }は{ a<X≦b }{ω∈Ω
| X (ω)∈B }は{ X∈B }などと略記される。
野田・宮岡『数理統計学の基礎』p15.
(random variable)、確率ベクトル(random vector)
標本空間Ω上の
標本空間Ω上の
つまり、
値域にどんなボレル集合をとっても、
その逆像がΩ上のσ集合族に属す。
そんな実数値集合関数のこと。
1:
⇔
X−1 ( (−∞,a ] ) ≡{ω∈Ω | −∞<X(ω)≦a}∈どんな風に実数
aを与えてやっても (−∞,a ]の逆像がΩ上のσ集合族に属す。※
∀a∈R1:「どんな風に実数aを与えてやっても」というところがポイント。※ボレル集合の理解が難しいようなら、
こちらの定理を確率変数の定義としたほうがいいかも。
※ 略記法
{ω∈Ω
| a<X(ω)≦b }は{ a<X≦b }{ω∈Ω
| X (ω)∈B }は{ X∈B }などと略記される。
野田・宮岡『数理統計学の基礎』p15.
2:
X−1 ( (−∞,a ] ) ≡{ω∈Ω | −∞<X(ω)≦a}∈
⇔ 任意の区間
I (閉区間、半開区間、開区間)に対して{ω∈Ω
| X(ω)∈I }∈
定理2の証明
アウトライン:
∀a∈R1 として、(−∞,a ]の逆像がΩ上のσ加法族に属すなら
任意の区間の逆像もΩ上のσ加法族に属し、その逆も成立。
[1] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、(a, ∞) の逆像もΩ上のσ加法族に属し、その逆も成立。 [2] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、
(−∞,b) の逆像もΩ上のσ加法族に属し、その逆も成立。 [3] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、
[b, ∞) の逆像もΩ上のσ加法族に属し、その逆も成立。 [4] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、
任意の閉区間の逆像もΩ上のσ加法族に属し、その逆も成立。
[5] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、任意の開区間の逆像もΩ上のσ加法族に属し、その逆も成立。
[6] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、半開区間
(a, b ] の逆像もΩ上のσ加法族に属し、その逆も成立。 [7] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、半開区間
[a, b ) の逆像もΩ上のσ加法族に属し、その逆も成立。[1] (−∞,a ]の逆像がΩ上のσ加法族に属すなら、
(a, ∞) の逆像もΩ上のσ加法族に属す。
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω | −∞<X(ω)≦a}∈これがσ加法族に属すということは、
その補集合もσ加法族に属すことを意味している。
∵
σ加法族の定義すなわち、
X−1 ( (−∞,a ] )C ≡{ω∈Ω | −∞<X(ω)≦a}C ∈
逆写像の性質から、
X−1 ( (−∞,a ] )C
= X−1 ( (−∞,a ] C )=X−1 ( (a, ∞) )≡{ω∈Ω | a<X(ω)<∞ }
なので、左辺を入れ替えて、
∴
X−1 ( (a, ∞) ) ≡{ω∈Ω | a<X(ω)<∞}∈逆も成り立つことは容易にわかる。
∵
X−1 ( (a, ∞) )がσ加法族に属すなら、その補集合もσ加法族に属す。∵
σ加法族の定義∵
逆写像の性質から、X−1 ( (a, ∞) )C=X−1 ( (a, ∞) C ) = X−1 ( (−∞,a] )
従って、以下の結論が得られる。
X−1 ( (−∞,a ] ) ≡{ω∈Ω | −∞<X(ω)≦a}∈
⇔
X−1 ( (a, ∞) ) ≡{ω∈Ω | a<X(ω)<∞}∈for ∀a∈R1
[2] (−∞,a ], for ∀a∈R1の逆像がΩ上のσ加法族に属すなら、
(−∞,b ) , for ∀a∈R1の逆像もΩ上のσ加法族に属す。
・X−1 ( (−∞,a ] )∈
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω | −∞<X(ω)≦a}∈どんな実数
aであれX−1 ( (−∞,a ] )がΩ上のσ加法族に属すというのだから、実数
aが、任意の実数b−1/1であれ、任意の実数
b−1/2であれ、任意の実数
b−1/3であれ、・
・
・
任意の実数
b−1/nであれ、・
・
・
X−1 ( (−∞,a ] )はΩ上のσ加法族に属す。
すなわち、
B1= X−1 ((−∞,b−1/1 ])≡{ω∈Ω | −∞<X(ω)≦b−1/1}∈
B2= X−1 ((−∞,b−1/2 ])≡{ω∈Ω | −∞<X(ω)≦b−1/2}∈
・
・
・
Bn= X−1 ((−∞,b−1/n ])≡{ω∈Ω | −∞<X(ω)≦b−1/n}∈
・
・
・
したがって、
σ加法族の定義から、 ![]() ∈
∈![]()
,for∀b∈R1
これは、
X−1 ((−∞,b))≡{ω∈Ω|−∞<X(ω)<b}に等しいので、∴
X−1 ((−∞,b))≡{ω∈Ω|−∞<X(ω)<b}∈
・X−1 ((−∞,b))∈
X−1 ((−∞,b))≡{ω∈Ω|−∞<X(ω)<b}∈
どんな実数
bであれ、X−1 ((−∞,b))がΩ上のσ加法族に属すというのだから、実数
bが、任意の実数a+1/1であれ、任意の実数
a+1/2であれ、任意の実数
a+1/3であれ、・
・
・
任意の実数
a+1/nであれ、・
・
・
X−1 ((−∞,b))はΩ上のσ加法族に属す。
すなわち、
A1= X−1 ((−∞, a+1/1))≡{ω∈Ω | −∞<X(ω) < a+1/1 }∈
A2= X−1 ((−∞, a+1/2))≡{ω∈Ω | −∞<X(ω) < a+1/2 }∈
・
・
・
An= X−1 ((−∞, a+1/n))≡{ω∈Ω | −∞<X(ω) < a+1/n }∈
・
・
・
σ加法族の定義から導出される定理から、
![]() ∈
∈![]()
for∀a∈R1
これは、
X−1 ( (−∞,a ] )≡{ω∈Ω | −∞<X(ω)≦a}に等しいので、∴
X−1 ( (−∞,a ] )≡{ω∈Ω | −∞<X(ω)≦a}∈従って、以下の結論が得られる。
X−1 ( (−∞,a ] )≡{ω∈Ω | −∞<X(ω)≦a}∈
⇔
X−1 ((−∞,b))≡{ω∈Ω|−∞<X(ω)<b}∈
[3] (−∞,a ]の逆像がΩ上のσ加法族に属すなら、
[b, ∞) の逆像もΩ上のσ加法族に属す。
(⇒)
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈[A-2]より、
X−1 ((−∞,b))≡{ω∈Ω|−∞<X(ω)<b}∈
これがσ加法族に属すということは、
その補集合もσ加法族に属すことを意味している。
∵
σ加法族の定義すなわち、
X−1 ( (−∞,b ) )C ≡{ω∈Ω | −∞<X(ω)<b}C ∈
逆写像の性質から、
X−1 ( (−∞,b ) )C
= X−1 ( (−∞,b ) C )=X−1 ( [b, ∞) )≡{ω∈Ω | b≦X(ω)<∞ }
なので、左辺を入れ替えて、
∴
X−1 ( [b, ∞) ) ≡{ω∈Ω | b≦X(ω)<∞}∈ ![]() 。
。
仮定:
X−1 ( [b, ∞) ) ≡{ω∈Ω | b≦X(ω)<∞}∈これがσ加法族に属すということは、
その補集合もσ加法族に属すことを意味している。
∵
σ加法族の定義すなわち、
X−1 ( [b, ∞) )C ≡{ω∈Ω | b≦X(ω)<∞}C∈
逆写像の性質から、
X−1 ( [b, ∞) )C
= X−1 ( [b, ∞)C )=X−1 ( (−∞,b) )≡{ω∈Ω | −∞<X(ω)<b }
なので、左辺を入れ替えて、
X−1 ((−∞,b))≡{ω∈Ω|−∞<X(ω)<b}∈
[A-2]より、
∴
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈従って、以下の結論が得られる。
X−1 ( (−∞,a] )≡{ω∈Ω | −∞<X(ω)≦a}∈
⇔
X−1 ( [ b,∞) )≡{ω∈Ω | b≦X(ω)<∞}∈[4] (−∞,a ]の逆像がΩ上のσ加法族に属すなら、
任意の閉区間の逆像もΩ上のσ加法族に属す。
(⇒)
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈b, c を、b < cを満たす任意の実数とする。
どんな実数
aであれX−1 ( (−∞,a ] )がΩ上のσ加法族に属すというのだから、実数
aが、それとは別の任意の実数cでもよい。X−1 ( (−∞,c ] )≡{ω∈Ω|−∞<X(ω)≦c}∈
また、
[A-3]から、X−1 ( [ b,∞) )≡{ω∈Ω | b≦X(ω)<∞}∈
σ加法族の定義から導出される定理から、
これらの共通部分もσ加法族に属す。すなわち、
X−1 ((−∞,c ])∩X−1 ([b,∞))={ω∈Ω|b≦X(ω)≦c}= X−1 ([b,c])∈
![]()
仮定:任意の閉区間を
In= [a-n,a], for∀a∈R1,for∀n∈R1とし、X−1 ( In )≡X−1 ( [a-n,a] )≡{ω∈Ω| a-n≦X(ω)≦a}∈
σ加法族の定義(条件3)から、
![]() ∈
∈![]()
ところが、この左辺を計算すると、
![]() =
=
∴
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈
[5] (−∞,a ]の逆像がΩ上のσ加法族に属すなら、
任意の開区間の逆像もΩ上のσ加法族に属す。
(⇒)
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈b を、a <bを満たす任意の実数とする。
[A-1]から、
X−1 ( ( a,∞) )≡{ω∈Ω|a<X(ω)<∞}∈
[A-2]から、
X−1 ( (−∞,b) )≡{ω∈Ω|−∞<X(ω)<b }∈
σ加法族の定義から導出される定理から、
これらの共通部分もσ加法族に属す。すなわち、
X−1 ((a,∞))∩X−1 ((−∞,b )) ={ω∈Ω| a<X(ω)<b }= X−1 ((a,b))∈
![]()
仮定:任意の開区間を
In= (a-n,a), for∀a∈R1,for∀n∈R1とし、X−1 ( In )≡X−1 ( (a-n,a) )≡{ω∈Ω| a-n<X(ω)<a}∈
σ加法族の定義(条件3)から、
![]() ∈
∈![]()
ところが、この左辺を計算すると、
![]() =
=
∴
X−1 ( (−∞,a ) )≡{ω∈Ω|−∞<X(ω)<a}∈[A-2]より、
∴
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈[6] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、
半開区間
(a, b ] の逆像もΩ上のσ加法族に属し、その逆も成立。(⇒)
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈b を、a <bを満たす任意の実数とする。
どんな実数
aであれX−1 ( (−∞,a ] )がΩ上のσ加法族に属すというのだから、実数
aが、それとは別の任意の実数bでもよい。X−1 ( (−∞,b] )≡{ω∈Ω|−∞<X(ω)≦b}∈
[A-1]から、
X−1 ( ( a,∞) )≡{ω∈Ω|a<X(ω)<∞}∈
σ加法族の定義から導出される定理から、
これらの共通部分もσ加法族に属す。すなわち、
X−1 ((a,∞))∩X−1 ((−∞,b]) ={ω∈Ω| a<X(ω)≦b }= X−1 ((a,b])∈
![]()
仮定:任意の開区間を
In= (a-n,a], for∀a∈R1,for∀n∈R1とし、X−1 ( In )≡X−1 ( (a-n,a] )≡{ω∈Ω| a-n<X(ω)≦a}∈
σ加法族の定義(条件3)から、
![]() ∈
∈![]()
ところが、この左辺を計算すると、
![]() =
=
∴
X−1 ( (−∞, a] )≡{ω∈Ω|−∞<X(ω)<a}∈[7] ∀a∈R1 として(−∞,a ]の逆像がΩ上のσ加法族に属すなら、
半開区間
[b, c ) の逆像もΩ上のσ加法族に属し、その逆も成立。(⇒)
仮定:
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈b を、a <bを満たす任意の実数とする。
[A−2] から、
X−1 ( (−∞,c) )≡{ω∈Ω|−∞<X(ω)<c}∈
[A−3]から、
X−1 ( [ b,∞) )≡{ω∈Ω|b≦X(ω)<∞}∈
σ加法族の定義から導出される定理から、
これらの共通部分もσ加法族に属す。すなわち、
X−1 ([b,∞))∩X−1 ((−∞,c)) ={ω∈Ω| b≦X(ω)<c }= X−1 ([b, c))∈
![]()
仮定:任意の開区間を
In= [a-n,a), for∀a∈R1,for∀n∈R1とし、X−1 ( In )≡X−1 ( [a-n,a) )≡{ω∈Ω| a-n≦X(ω)<a}∈
σ加法族の定義(条件3)から、
![]() ∈
∈![]()
ところが、この左辺を計算すると、
![]() =
=
∴
X−1 ( (−∞, a) )≡{ω∈Ω|−∞<X(ω)<a}∈[A-2]より、
∴
X−1 ( (−∞,a ] )≡{ω∈Ω|−∞<X(ω)≦a}∈
※
柳川『統計数学』pp.11-12にでている証明の省略された部分を自力で埋めてみた。
定理1の証明
(proof)
(⇒)
Xは標本空間Ω上の確率変数とする。
すなわち、
XはΩ上のすなわち、
X−1 (B)∈ここで、上記の
Bについて。(−∞,a ] ∈
B=(−∞,a ] ととっても相変わらず上式は成立する。
∴
X−1 ( (−∞,a ] )∈ ![]()
※具体例
(柳川『統計数学』p.11)※
野田・宮岡『数理統計学の基礎』pp.14-15、鈴木・山田『数理統計学―基礎から学ぶデータ解析―(第二版)』での、確率変数の定義とその必要十分条件となる上記定理。しかし、柳川『統計数学』pp.11-13.と佐藤『はじめての確率論 測度から確率へ』pp.34-37.では、定理と定義が逆になっている。
X=(X1,X2,…,Xn)は
⇔
Xi は(講義ノートから、出所不明)
Borel可測
f : R n → Rm はBorel可測
⇔
f-1(B)≡{ x∈ R n | f ( x ) ∈ B }∈※連続関数なら
Borel可測。Xを
h : R → R はBorel可測関数であれば、
Y= h (X)
も確率変数。
(証明)
Yが確率変数の定義を満たすことを示せばよい。写像
Y: Ω∋ω→h [X(ω)]∈Rを考える。各
B∈Y−1 (B) = X−1[ h−1 (B) ]
仮定より、
h : R → R はBorel可測関数なので、h−1 (B) ∈仮定より、
Xはゆえに、
Y−1(B)=X−1[ h−1 (B) ] ∈∴
Yは
(参考文献
)野田・宮岡『数理統計学の基礎』pp.15-16は、一次関数のケースのみ。ボレル集合の知識不要。Pp.24-25はきわめて有用。
柳川堯『統計数学』近代科学社、1990, pp.13-14.は、確率変数の関数が確率変数になる条件を、一般的に論じている。ボレル集合の知識が必要。
佐藤『はじめての確率論 測度から確率へ』pp.38-39.
(
reference)文献
1.『岩波数学辞典(第三版)』項目47C(p.128), 225B. (pp.626-627)文献
2. 佐藤坦『はじめての確率論 測度から確率へ』共立出版、1994、pp.34-44.文献
3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―(第二版)』内田老鶴圃、1998年、pp.21-22。文献
4. 矢野・田代『社会科学者のための基礎数学 改訂版』裳華房、1993年、p.150-155.文献
5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、pp.3-4, pp.14-15, pp.24-25 。文献
6. 柳川堯『統計数学』近代科学社、1990, pp.11-14.