確率の定義

　　　　Aの上の実数値集合関数

定義：確率測度 (Probability Measure)、確率(Probability)、 確率空間(probability space)・確率モデル(probability model)、確率の公理(probability axioms)

　　　　　(Ω, A)：可測空間、

　　　　　Aの上の実数値集合関数P: A∋AP(A)∈R

　　　　とする。

　　　　

　　　　Pが以下の(P1)〜(P3)を満たす

　　　　　　(P1)　0≦P(A)≦1 ∀A∈A

　　　　　　(P2)　P(Ω)=1

　　　　　　(P3)　A1,A2,…∈A, Ai∩Aj=φ (i≠j) ⇒

　　　　　　　　　　　　　　　　　　　　　(完全加法性/可算加法性)

　　　　⇔

　　　　・Pを、(Ω, A)上の確率測度(probability measure)ないし確率(probability)と呼ぶ。

　　　　・組(Ω, A, P )を、確率空間(probability space)あるいは確率モデル(probability model)と呼ぶ。

　　　　・A∈Aに対し、確率Pの値P(A)を、事象Aの起こる確率と呼ぶ。

　　　　

　　　　・(P1)〜(P3)を確率の公理(probability axioms)と呼ぶ。

（reference）

文献1.『岩波数学辞典（第三版）』項目47.B. (pp.127-128).

文献2. 佐藤坦『はじめての確率論　測度から確率へ』共立出版、1994、pp.18-24.

文献3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、pp.7-12。

文献4. 矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p.148-150.

文献5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.2 。

文献6. 柳川堯『統計数学』近代科学社、1990, pp.3-4.

確率についての諸定理

1. 空事象φの確率P(φ)

　　　　P(φ)=0

　　　　(proof)

　　　　確率の定義(P1)より、0≦P(φ)≦1　　…(1)

　　　　φ=φ∪φ∪φ…　かつ　φ∩φ=φ　であるので、確率の定義(P3)より、

　　　　P(φ)=P(φ∪φ∪φ…)=P(φ)+ P(φ)+…

　　　　仮に、0<P(φ)≦1とすると、右辺が収束せず、(1)と矛盾をきたす。

　　　　したがって、P(φ)=0

（reference）

佐藤坦『はじめての確率論　測度から確率へ』共立出版、1994、p20

鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、p.10,

野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.5

は、同様の証明。

柳川堯『統計数学』近代科学社、1990,p.4.は異なった証明。

2. 有限加法性(Finite Additivity)

　　　　A1,…..,An∈A, Ai∩Aj=φ(i≠j)

　　　　⇒

(proof)

　　　　An+1＝An+2＝…=φ∈Aとする。(1)

　　　　　　∵(1)

　　　　

　　　　　　　∵A1,…..,An, An+1,An+2,…∈A, Ai∩Aj=φ(i≠j)にたいして、

　　　　　　　　確率の定義(P3)完全加法性を適用

　　　　

　　　　 ∵空事象φの確率

（reference）

同様の証明を

佐藤坦『はじめての確率論　測度から確率へ』共立出版、1994、.p21、pp.10,

野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.5

は詳細に示し、

柳川堯『統計数学』近代科学社、1990,p.4.

は方向性だけ示唆。

3-1.単調性(monotonicity)

　　　　A⊂B　⇒　P(A)≦P(B)

(proof)

　　　　A⊂Bより、

　　　　　　B=A∪ (B−A).

　　　　　　A ∩(B−A)=φ （互いに排反）

　　　　したがって、確率の有限加法性より、

　　　　　　P(B)=P(A∪(B−A))=P(A)+P(B−A)

　　　　確率の定義P1より、P(B−A)≧0

　　　　∴P(B)≧P(A)

（reference）

同様の証明を

野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.6

3-2.差法可能性(subtractability)

　　　　A⊂B　⇒　P(B−A) = P(B)−P(A)

(proof)

　　　　A⊂Bより、

　　　　　　B=A∪(B−A).

　　　　　　A ∩(B−A)=φ （互いに排反）

　　　　したがって、確率の有限加法性より、

　　　　　　P(B)=P(A∪(B−A))=P(A)+P(B−A)

　　　　両辺からP(A)を引いて、

　　　　　　P(B)−P(A)= P(B−A)

（reference）

野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.6

3-3.余事象(complementary event)の確率

　　　　P(Ac)=1−P(A)

　　　　(proof)

　　　　Ω=A∪ Ac

　　　　確率の有限加法性より、

　　　　P(Ω) = P(A∪Ac) = P(A) ＋ P(Ac)

　　　　確率の定義P2より、左辺=1となるので、

　　　　1 = P(A) ＋ P(Ac)

　　　　∴　P(Ac) = 1 − P(A)

（reference）

鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、p.10.

矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p149

が同様の説明。

野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、p.6は、3-2差分可能性の系として示す(B=Ωとおけば、B−A=Ω−A=Acとなるので)。

5.劣加法性

　　　　A1, A2,,…∈A [注:Ai∩Aj=φが条件に入ってない]⇒

　　　　(proof)　

　

加法則(additon rule)

　　　　A,B∈Aならば、

　　　　P(A∪B)=P(A)+(B)−P(A∩B)

　　　　

　　　　(proof)

　　　　

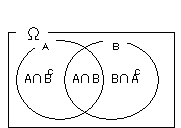
　　　　(a)　準備その１　　

　　　　まず、A∩Bc、B∩Ac、A∩Bについて、

　　　　確率の有限加法性を適用する条件が整っていることを示す。

　　　　　　・A,B∈Aより、Ac,Bc∈A 　∵σ加法族の定義(条件2)

　　　　　　　よって、A∩Bc、B∩Ac、A∩B∈A 　

　　　　　　　　　　　∵可測空間に関する諸定理(3) (An+1以降をφとおいて)。

　　　　　　・A∩Bc、B∩Ac、A∩Bは互いに排反。∵ベン図を見よ。

　　　　(b)　準備その２　　

　　　　次に、考察の対象となる事象を、
　　　　確率の有限加法性を適用可能な上記事象の和として表す。

　　　　A∪B = (A∩Bc)∪(B∩Ac)∪(A∩B)

　　　　　　A= (A∩Bc)∪(A∩B)

　　　　　　B= (B∩Ac)∪(A∩B)

　　　　(ｃ)　準備その3

　　　　考察の対象となる事象の確率を、確率の有限加法性を用いて分解する。

　　　　　<c-1>

　　　　　P(A∪B)=P[(A∩Bc)∪(B∩Ac)∪(A∩B)]　　∵(b)

　　　　　　　　　=P(A∩Bc)+P(B∩Ac)+P(A∩B)　　∵(a)ヨリ確率の有限加法性を適用

　　　　　<c-2>

　　　　　　　P(A)=P[(A∩Bc)∪(A∩B)]　　∵(b)

　　　　　　　　=P(A∩Bc)+P(A∩B)　　∵(a)ヨリ確率の有限加法性を適用

　　　　　<c-3>

　　　　　　　P(B)=P[(B∩Ac)∪(A∩B)]　　∵(b)

　　　　　　　　　=P(B∩Ac)+P(A∩B)　　∵(a)ヨリ確率の有限加法性を適用

　　　　(d)　本題

　　　　P(A∪B)=P(A∩Bc)+P(B∩Ac)+P(A∩B)　∵<c-1>

　　　　　　　=[P(A)−P(A∩B)]+[P(B)−P(A∩B)] +P(A∩B)　

　　　　　　　　　　　　∵<c-2>、<c-3>で、P(A∩B)を移項した表現

　　　　　　　　　　　　　P(A∩Bc)= P(A)−P(A∩B)、

　　　　　　　　　　　　　P(B∩Ac)=P(B)−P(A∩B)

　　　　　　　　　　　　　ヨリ

　　　　　　　=P(A) +P(B)−P(A∩B)

　　　　

　　　　

  1. 確率の連続性

　　　　{An}⊂Aが単調増大列または単調減少列のとき、

　　　　

　　　　基礎知識→極限集合　

(i)下からの連続性(continuity from below)

　　　　{An}⊂Aが単調増大列⇒

　　　　（解釈）「増大事象列An, n=1,2,…にたいして、P(An)は増大しながら、

　　　　　　　　　　　　

　　　　　　　　　に収束する。」[西尾pp.33-34]

　　　　(proof)

　　　　　準備1:

　　　　　　　仮定より、{An}⊂Aは単調増大列。

　　　　　　　増大列の極限についての定理から、{An}には極限が存在し、

　　　　　　　　(＊)

　　　　　準備２：

　　　　　　　{Bi}を、

　　　　　　　B1=A1

　　　　　　　B2=A2−A1

　　　　　　　：

　　　　　　　

　　　　　　　：

　　　　　　　とおく。

　　　　　　　

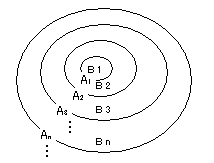
　　　　　　　すると、

　　　　　　・Bi ∈A　( i=1,2,…)

　　　　　　　　　なぜなら、

　　　　　　　　　仮定よりB1=A1∈A　

　　　　　　　　　Bi ＝Ai−Ai−1＝Ai ∩ (Ai−1)C　( i = 2,3,4,…)　　　

　　　　　　　　　　　　ここで、仮定よりAi ∈A　(1)

　　　　　　　　　　　　(1)とσ加法族の定義（条件3）より

　　　　　　　　　　　　(Ai−1)C　∈A　(2)

　　　　　　　　　　　　σ加法族は有限のintersectionについて閉じているので、

　　　　　　　　　　　　(1)と(2)より、

　　　　　　　　　　　　Ai ∩ (Ai−1)C　∈A　

　　　　　　Bi ∩ B j＝φ　（i≠j）　[排反](＊＊)

　　　　　　・　　　(＊＊＊)　

　　　　　　・　　　　(＊＊＊＊)

　　　　　　

　　　　　　(＊)

　　　　　　　　　　　　(＊＊＊＊)

　　　　　　　　　　　　(＊＊)より確率の公理(P3)確率の完全加法性を適用

　　　　　　　　　　　　　つまりP(B1)+P(B2)+P(B3)+…

　　　　　　　　　　　

　　　　　　　　　　　　　つまりn→∞での[P(B1)+P(B2)+…+P(Bn)]

　　　　　　　　　　　(＊＊)より確率の有限加法性を適用　　

　　　　　　　　　　　↑この辺り納得いかんが、野田宮岡によると、こうなってる。

　　　　　　　　　　　　　(＊＊＊)　より

　　　　

　　　　

(ii)上からの連続性(continuity from above)

　　　　{An}⊂Aが単調減少列⇒　

　　　　（解釈）「減少事象列An, n=1,2,…にたいして、P(An)は減少しながら、

　　　　　　　　　　

　　　　　　　　　に収束する。」[西尾p.34]

　　　　　　　　　

　　　　(proof)

　　　　　準備1:

　　　　　　　仮定より、{An}⊂Aは単調減少列。

　　　　　　　減少列の極限に関する定理から、{An}には極限が存在し、

　　　　　　　　(1)

　　　　　準備２：

　　　　　　　{Bi}を、

　　　　　　　B1= A1−A2

　　　　　　　B2=A3−A2

　　　　　　　：

　　　　　　　Bn=An−An+1

　　　　　　　：

　　　　　　　とおく。

　　　　　　　（An+1がないとBnは定義されない。

　　　　　　　　つねに、{ Ai }のほうが{ Bi }よりも一歩先まであることに

　　　　　　　　注意せよ）

　　　　　

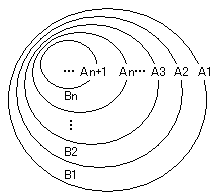
　　　　　　　すると、

　　　　　　・Bi ∈A　( i=1,2, 3,…) (2)

　　　　　　　　　なぜなら、

　　　　　　　　　　　　仮定よりAi ∈A　(a)

　　　　　　　　　　　　(1)とσ加法族の定義（条件3）より

　　　　　　　　　　　　(Ai)C　∈A　(b)

　　　　　　　　　　　　σ加法族は有限のintersectionについて閉じているので、

　　　　　　　　　　　　(a)と(b)より、

　　　　　　　　　　　　Ai ∩ (Ai+1)C　∈A　

　　　　　　　　　ゆえに、

　　　　　　　　　Bi ＝Ai−Ai+1＝Ai ∩ (Ai+1)C　∈A　( i = 1,2,3,…)　　　

　　　　　　・、{Bi}は互いに素。　(3)

　　　　　　・　と書ける。(4)

　　　　　　・　　　　∵{ Bi }の定義

　　　　　　　　∵Ai⊃Ai+1より確率の差分可能性適用　

　　　　　　　

　　　　　　

　　　　　　　　　　　　　（５）

　　　　（本題）

　　　　　　　　(4)ヨリ

　　　　　　　　　　(2) (3)より

　　　　　　　　　　　　　　　　　　　　　確率の公理(P3)確率の完全加法性を適用

　　　　　　　　　　(5)ヨリ

　　　　　∴

　　なんか納得できない。P( lim An )とlim P(An)の記法の違いでごまかされている気がする。両者の間に、記法の違い以外に、どのような実質的な意味の違いがあるというのだろうか。LimAnの定義は、極限集合ではっきり定義されている（ここでは∩Anになる）。limP(An)の定義は？

（reference）

文献1.『岩波数学辞典（第三版）』項目47.B. (pp.127-128).

文献2. 佐藤坦『はじめての確率論　測度から確率へ』共立出版、1994、pp.20-24.

文献3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―（第二版）』内田老鶴圃、1998年、pp.9-12。

文献4. 矢野・田代『社会科学者のための基礎数学　改訂版』裳華房、1993年、p.148-150.

文献5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、pp.5-8 。

文献6. 柳川堯『統計数学』近代科学社、1990, pp.4-6.

文献7. 西尾真喜子『確率論』実教出版社、1978, pp.32-34.