可測空間
標本空間:Ω、A:Ωの部分集合族(Ωの部分集合を元とする集合)とする。
AはΩ上のσ加法族
⇔
Aは以下の3条件を満たす。(条件1) Ω∈A
(条件2) A∈A ⇒ Ac∈A
(条件3) A1, A2, …∈A ⇒
(たとえ
AがΩのあらゆる部分集合全体からなる集合族でなくても)事実
→野田・宮岡『
数理統計学の基礎』p. 3 。集合Ωにおける完全加法族として最小のもの:
{φ
,Ω}{φ
,Ω}⊂A集合Ωにおける完全加法族として最大のもの:
Ωのすべての部分集合の族。
2Ωと記す。
![]()
・「Ωの部分集合からなる任意の族
A0が与えられていると、A0を含む最小の完全加法族が存在し、これをA [A0]と記す。
A0⊂2Ωであるから、A0を含む完全加法族Aの全体{ A }を考え、
それらすべての共通部分∩{
A } AをA [A0]と記すことにすれば、A [A0]が完全加法族の条件を満たすことは容易にみられる。」
野田・宮岡『数理統計学の基礎』p. 3 。
・Ωの任意の部分集合族
Sを含む最小のΩ上のσ集合体σ[S](佐藤『はじめての確率論 測度から確率へ』pp.11-13[定理2.1])
「
SをΩの任意の部分集合族(σ集合体でなくてもいい)とする。このとき「部分集合族
Sを含む」「最小の」
「Ω上のσ集合体」が
「一意的」に
存在する。
これをσ
[S]と書き、部分集合族
Sから生成されるΩ上のσ集合体という。すなわち、
(1) σ[S]はΩ上のσ集合体
(2) S⊂σ[S]
(3)
を満たすΩの部分集合族σ
[S]が一意的に存在する。[証明]
」
Ω上のσ集合族Aの要素、すなわち、
A∈A
を事象という。
(Ωの部分集合達のうち、
確率を定義可能な部分集合達、すなわち、
σ集合族Aであるための条件を満たす部分集合達
と理解すればいいらしい)
事象・σ加法族の定義に関する解釈
文献
2での説明「このように考えてみると、サイコロの二回投げについて、あることがらの確率を計算するためには、まずそのことがらに対応する
標本空間Ωの部分集合を考え、つぎにその部分集合について確率を計算すればよいことがわかる。標本空間 =起こりうる全ての結果の集合
∪
部分集合 ←確率を計算したいことがら
↓
確率
」
(p.4)「このように銅貨の
n回投げの場合にも、いろいろなことがらの確率を計算するためには、まず標本空間の対応する部分集合を求め、つぎにその部分集合についての確率を計算すればよいことがわかる。」(p.5)「しかしながら、銅貨の無限回投げでは
標本空間Ω∞は無限集合、したがって、その部分集合も一般には無限集合である。その確率を銅貨のn回投げと同じように定めようとすると…..となって意味がわからない。にもかかわらず一点だけからなる集合{ω}についてはP(ω)=0、標本空間全体Ω∞についてはP(Ω∞)=1、また上に述べたような典型的な部分集合AやBについてあP(A)=1/4、P(B)=1/8であってほしい。そこでΩ∞の部分集合に対して、このような確率が何等かの方法で定義できるか?という問題が起こる。実はこのような確率は存在する。しかしサイコロの2回投げや銅貨のn回投げと違って、もはやΩ∞のすべての部分集合に対しては定義されない。そこで銅貨の無限回投げで、あることがらの確率を考えるには、まずそのことがらに対応するΩ∞の部分集合に対して確率が定義されているかどうかをまず確かめねばならない。」(pp.6-7)「前節で述べたように
標本空間Ω上の確率は、Ωの全ての部分集合に対して定義されているとは限らない。それではどのような部分集合に確率は定義されるのであろうか?….それでは確率の定義される標本空間の部分集合はどのようにして特徴付けられるのであろうか?確率の定義されている部分集合全体は『σ-集合体』として特徴付けられる。」(p.7)「Ωを空でない集合とする。これは有限集合でもよいし、無限集合でもよい。さて、このΩを標本空間として、その部分集合に対して確率を定義したいのであるが、先にも述べたように、一般には、確率はΩのすべての部分集合に対して定義されているわけではない。そこで
確率の定義されているΩの部分集合全体をBとすると、Bはどのように特徴付けられるであろうか?まず、標本空間全体の確率は当然1と考えられるから全体集合Ωには確率が定義されてP(Ω)=1、したがってΩ∈Bとなる。つぎに、ある部分集合A⊂Ωに確率P(A)が定義されていれば、Ac=Ω\AについてはP(Ac)=1−P(A)と考えられるからAc∈Bとなる。それからもう一つ、部分集合列An、n∈Nにそれぞれ確率が定義されているとき、 和集合(略:σ集合体の三条件の記述)
一般に
(B1)(B2)(B3)を満たすΩの部分集合の集まり(部分集合族)BをΩ上のσ集合体という。いいかえると、Ωを標本空間とする確率はΩ上のσ-集合体の上に定義されている。」(p.8)文献
5での説明「現れた『事象』は試行などの結果したがって標本空間の要素(標本点と呼ばれる)を含む
標本空間のある種の部分集合として記述すると便利であり、そのとき事象とよばれる。このような事象の族を定義することから始める。….Ωを空でないある集合として、その部分集合のある族Aが条件…..を満たすとき、Aを完全加法族、σ-集合体、σ-代数などとよぶ。」文献
6での説明「確率はある1つのことがら、あるいはことがらの集合に対して定義される。いいかえれば、そのようなことがらの全体からなる集合をΩとするとき、
確率はΩの部分集合に対して定義される。確率をきちんと定義するには、その上に確率が定義されるべき土俵、つまり部分集合の集合を、まず整備しておく必要がある。それが、つぎのσ集合族である。……..確率論では、σ集合族Bの要素を事象という。とくに、Ωを全事象、φ=Ωcを空事象という。これらは、集合論でいう部分集合、全集合、空集合である。」(p.2)
II.
可測空間ΩとAの対(Ω, A)を可測空間(measurable space)という。
(Ω, A):可測空間 (1)
φ∈A (2)
A1,A2,…,An∈A ⇒
A1,A2,…,An,…∈A ⇒
A1,A2,…, An∈A ⇒
[証明]
AはΩ上のσ加法族とされているので、
Aはσ加法族の定義(条件1〜3)を満たしている。
(1)
AはΩ上のσ加法族とされているので、
σ加法族の定義(条件1)より Ω∈A 。
σ加法族の定義(条件2)を用いると、
Ω∈A ⇒ Ωc=φ∈A
(2)
An+1=An+2=…=φ∈A (*)
とおく。これらもσ集合族と考えてよいのは、
上記(1)による。すると、A1,…,An,An+1,…∈A
σ加法族の定義(条件3)より、
このとき、
(*)より、∴
※参照:
柳川『統計数学』, p.3(3)
A1,A2,……∈A
⇒
A1c, A2c, ……∈A [σ加法族の定義(条件2)ヨリ] ⇒ ![]() ∈
∈
⇒ 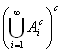 ∈
∈
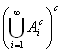
=
であるので、
![]() =
=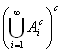 ∈
∈
(4)
An+1=An+2=…=φ∈A (*)
とおく。これらもσ集合族と考えてよいのは、
上記(1)による。すると、A1,…,An,An+1,…∈A
上記(3)より、
![]() ∈
∈
このとき、
(*)より、 ![]() なので、
なので、
∴![]() ∈
∈
※参照:
柳川『統計数学』演習問題1.A.3. III.事象関連の用語「事象」:
標本空間Ωの部分集合※だからといって、なんでも部分集合なら事象というわけではないのは、
厳密な事象の定義→Ω上のσ加法族の定義でみたとおり。 Aが起こる」:試行の結果、事象
A=「標本空間Ωの部分集合A」に含まれる※なぜ
標本空間Ωも事象といってよいのか?→
厳密な事象の定義→Ω上のσ加法族の定義(条件1)と見てゆくべし。 (empty event): 空集合φ※なぜ空集合φも事象といってよいのか?
→
厳密な事象の定義→可測空間の性質(1)→Ω上のσ加法族の定義(条件1,2) と見てゆくべし。 Aと事象Bの和事象」(sum event) A∪B : Ωの元のうち、AまたはBに属すもの※部分集合
A,部分集合Bが事象といいうるなら、A∪Bも事象といってよいのはなぜ?→
厳密な事象の定義→可測空間の性質(2)→Ω上のσ加法族の定義と見てゆくべし。 Aと事象Bの積事象」(intersection, product event) A∩B: Ωの元のうち、Aに属し、なおかつ、Bに属すもの Aと事象Bは互いに排反」(exclusive events) A∩B=φ集合論でいうところの、「
互いに素」 Aの余事象(complementary event)A
c : Ωに属すうちで、Aには属さぬ元。集合論でいうところの、「
Aの補集合」。※
Aが事象なら、Aの補集合も、事象といってよいのはなぜ?→
厳密な事象の定義→Ω上のσ加法族の定義(条件2) A,B⊂Ωに対して差事象 B−A = { ω∈Ω | ω∈B, (","="&")
(
reference)文献
1.『岩波数学辞典(第三版)』項目47.B. (pp.127-128), 225(p.626)文献
2. 佐藤坦『はじめての確率論 測度から確率へ』共立出版、1994、pp.7-11.文献
3. 鈴木武・山田作太郎『数理統計学―基礎から学ぶデータ解析―(第二版)』内田老鶴圃、1998年、pp.5-7。文献
4. 矢野・田代『社会科学者のための基礎数学 改訂版』裳華房、1993年、p.148.文献
5. 野田一雄・宮岡悦良『数理統計学の基礎』共立出版、1992年、pp.1-3 。文献
6. 柳川堯『統計数学』近代科学社、1990, pp.2-3.