定義：実ベクトル空間における内積 inner product
[斎藤『線形代数入門』４章§6計量線形空間(p.120);神谷浦井『経済学のための数学入門』§3.2.3(p.124);永田『理系のための線形代数の基礎』4.1(p.114);志賀『ベクトル解析30講』第11講(pp.78-80);佐武『線形代数学』Ⅲ§6(p.117);砂田『行列と行列式』§7.1(p.238);志賀『固有値問題30講』8講(p.61);ホフマン・クンツェ『線形代数学Ⅱ』8.1内積(p.92); ]
【舞台設定】
R：実数体R
V：実ベクトル空間
【本題】
実ベクトル空間Vに属す任意の２つのベクトルx,yに対して、実数〈x,y〉を定める関係があって、
次の[要件1]～[要件4]を満たすとき、
〈x,y〉を、xとyの内積inner productとよぶ。
[要件1：線形性1] 任意のx1,x2,y∈Vにたいして、〈x1+x2,y〉＝〈x1,y〉＋〈x2,y〉
任意のx,y1,y2∈Vにたいして、〈x, y1+y2〉＝〈x,y1〉＋〈x, y2〉
論理記号で表すと、∀x1,x2,y∈V ( 〈x1+x2,y〉＝〈x1,y〉＋〈x2,y〉 )
∀x,y1,y2∈V ( 〈x, y1+y2〉＝〈x,y1〉＋〈x, y2〉 )
[要件2：線形性2] 任意のx,y∈V と任意の実数 a にたいして、〈ax,y〉=a〈x,y〉, 〈x,ay〉=a〈x,y〉
論理記号で表すと 、∀x,y∈V ∀a∈R ( 〈ax,y〉=a〈x,y〉かつ 〈x,ay〉=a〈x,y〉 )
[要件3：正値性] 任意のx∈Vにたいして、〈x,x〉≧０ であって、
〈x,x〉=０となるのはxが零ベクトルである場合のみに限る。
論理記号で表すと、∀x∈V ( ( 〈x,x〉≧０ ) かつ (〈x,x〉=０ ⇔ x=０) )
あるいは、∀x∈V ( ( 〈x,x〉≧０ ) かつ (x≠０⇒〈x,x〉>０) )
[要件4：対称性] 任意のx,y∈V にたいして、〈x,y〉=〈y,x〉
論理記号で表すと 、∀x,y∈V ( 〈x,y〉=〈y,x〉 )
※内積の性質
※内積によって定義される概念：内積により定まるノルム、ベクトルの直交、ベクトルのなす角
※下位概念：実n次元数ベクトル空間における内積
定義：計量実ベクトル空間・実計量線形空間・内積空間 metric vector space
[斎藤『線形代数入門』４章§6計量線形空間(p.120);神谷浦井『経済学のための数学入門』§3.2.3(p.124);永田『理系のための線形代数の基礎』4.1(p.114);佐武『線形代数学』Ⅲ§6(p.117);砂田『行列と行列式』§7.1(p.238);ホフマン・クンツェ『線形代数学Ⅱ』8.2内積空間(p.98); ]
【舞台設定】
R：実数体R
V：実ベクトル空間
【本題】
計量実ベクトル空間(計量線形空間・内積空間)とは、内積の定義された実ベクトル空間のことをいう。
※下位概念：実n次元数ベクトル空間に内積をさだめてつくった計量実ベクトル空間
定義：内積により定まるノルム norm
[斎藤『線形代数入門』４章§6計量線形空間(p.120);神谷浦井『経済学のための数学入門』§3.2.3(p.124);永田『理系のための線形代数の基礎』4.1(p.114);砂田『行列と行列式』§7.1(p.239);志賀『ベクトル解析30講』第11講(pp.78-80);志賀『固有値問題30講』8講(p.61);ホフマン・クンツェ『線形代数学Ⅱ』8.1内積(p.91); ]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
【本題1】
計量実ベクトル空間Vに属すベクトルxのそれ自身との内積の平方根
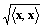
は、ノルムの定義を満たす。
※なぜ？
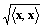・は、内積の要件3より、ノルム定義の第1要件を満たす。
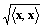・は、内積の性質によって、ノルム定義の第2要件を満たす。
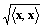・は、内積の性質によって、ノルム定義の第3要件を満たす。
【本題2】
・計量実ベクトル空間Vに属すベクトルxのそれ自身との内積の平方根
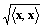
を、内積により定まるノルムと呼ぶ。
・ベクトルxの内積により定まるノルム・長さを、記号「∥x∥」で表す。
・つまり、任意のx∈Vにたいして、
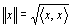
【本題3】
・計量実ベクトル空間Vに、内積により定まるノルム∥ ∥を定義することによって
組（V,∥ ∥ ）はノルム空間となる。
定義：単位ベクトル
[砂田『行列と行列式』§7.1(pp.241-2);]
【舞台設定】
R：実数体R
V：実ベクトル空間
x,y：実ベクトル空間Vに属すベクトル
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
∥x∥ ：計量実ベクトル空間Vにおけるベクトルxのノルム
【本題】
計量実ベクトル空間Vにおける単位ベクトルとは、 ∥x∥=1を満たすベクトルxのこと。
定理：単位ベクトル化
[永田『理系のための線形代数の基礎』補題4.2.1(p.116);]
【舞台設定】
R：実数体R
V：実ベクトル空間
x,y：実ベクトル空間Vに属すベクトル
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
∥x∥ ：計量実ベクトル空間Vの内積により定まるノルム
(本題1)
任意のベクトルx∈Vについて、
xが零ベクトルでないならば、
「xのノルムの逆数（スカラーになる）」と、ベクトルxとのスカラー積
( 1/∥x∥ ) x
は、
ノルム1のベクトルになり、
xと直交する全てのベクトルと直交する。
以上を論理記号でかくと、
（∀x∈V）（ x≠〇 ⇒ ∥ ( 1/∥x∥ ) x ∥=１ ）
（∀x,y∈V）（ x≠〇かつ〈x,y〉＝0 ⇒ 〈 ( 1/∥x∥ ) x, y 〉 ＝0 ）
(本題2)
( 1/∥x∥ ) xをつくることを、xの単位ベクトル化という。
※どうして、∥ ( 1/∥x∥ ) x ∥=１ といえるのか？→詳細
※どうして、( 1/∥x∥ ) xは、xと直交する全てのベクトルと直交するといえるのか？
・ノルムであるための要件1：非負性より、 x≠〇ならば、∥x∥>０
したがって、 x≠〇ならば、1/∥x∥ >０ …(1)
・〈 ( 1/∥x∥ ) x, y 〉 =( 1/∥x∥ ) 〈x,y〉=〈x,y〉/∥x∥ …(2)
∵内積であるための要件2:線形性2
・ x≠〇かつ〈x,y〉＝0 ならば、任意のベクトルx,yにたいして、(1)(2)と〈x,y〉＝0より、
〈 ( 1/∥x∥ ) x, y 〉 =0
が成り立つ。
つまり、x≠〇ならば、xと直交する全てのベクトルと、( 1/∥x∥ ) xは、xと直交する。
定義：ノルムから定められる距離
[神谷浦井『経済学のための数学入門』§3.2.3(p.123);松坂『集合・位相入門』§5-A(p.277);
矢野『距離空間と位相構造』1.1.1距離関数(p.5);志賀『固有値問題30講』8講(p.61);
ホフマン・クンツェ『線形代数学Ⅱ』8.2練習問題4(p.110); ]
【舞台設定】
R：実数体R
V：実ベクトル空間
x,y：実ベクトル空間Vに属すベクトル
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
∥x∥ ：計量実ベクトル空間Vにおけるベクトルxのノルム
（V,∥∥）：計量実ベクトル空間Vに、内積により定まるノルム∥ ∥を定義した、ノルム空間
(本題1)
実ベクトル空間Vに属す任意のベクトルx, yに対し、
ベクトルxと ベクトルyの逆ベクトルの和について、内積により定まるノルムをとると、
Vにおけるx, y間の距離の定義を満たす。
すなわち、
実ベクトル空間Vに属す任意のベクトルx, yに対し、
d(x, y)=∥x－y∥
とおくと、d(x, y)は、Vにおけるx, y間の距離の定義を満たす。
※なぜ？→証明
(本題2)
・計量実ベクトル空間Vに、上記の距離d(x, y)を定義することによって
組（V,d）は距離空間となる。
定理：計量実ベクトル空間、ノルム空間、距離空間
[砂田『行列と行列式』§7.1(a)定理7.9 (pp.240-1).。]
・計量実ベクトル空間Vに、内積により定まるノルム∥ ∥を定義することによって
組（ V, ∥ ∥ ）はノルム空間となる。
・計量実ベクトル空間Vは、内積により定まるノルムにより定まる距離によって、距離空間となる。
定義：直交する orthogonal
[斎藤『線形代数入門』４章§6計量線形空間(p.120);神谷浦井『経済学のための数学入門』§3.2.3(p.125);永田『理系のための線形代数の基礎』4.1(p.114);志賀『ベクトル解析30講』第11講(p.80);志賀『固有値問題30講』9講(p.67);。]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
【本題】
・実ベクトル空間Vに属すベクトルx,yが直交するとは、ベクトルx,yの内積がゼロであるということ。
・ベクトルx,yが直交することを、記号「x⊥y」で表す。
・つまり、x⊥y ⇔ 〈x,y〉＝0
※活用例：直交系、正規直交系、直交基底、正規直交基底
定義：ベクトルのなす角angle
[永田『理系のための線形代数の基礎』4.1(p.115);志賀『ベクトル解析30講』第11講(pp.79-80);]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
∥x∥ ：計量実ベクトル空間Vにおけるベクトルxのノルム
【本題】
・
※ベクトル空間の例：数ベクトル空間（実ベクトル空間、複素ベクトル空間）、K上の多項式関数の空間、
(reference)
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目317バナッハ空間(pp.922-):ノルムとノルム空間の解説が含まれている;項目341ヒルベルト空間B.(pp.1006-7)：内積の定義が含まれている.
線形代数のテキスト
ホフマン・クンツェ『線形代数学Ⅱ』8.1内積(pp.91-7);8.2内積空間(pp.98-111)培風館、1976年。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、4.1内積(p.114);。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.117)。
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年。
志賀浩二『数学30講シリーズ：ベクトル解析30講』朝倉書店、1988年、第11講(pp.78-80)。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年。
斎藤正彦『線形代数入門』東京大学出版会、1966年、４章§6計量線形空間(p.120)。
砂田利一『現代数学への入門：行列と行列式』2003年、§7.1-(a)内積 (pp.238-9).
解析学のテキスト
杉浦光夫『解析入門I』東京大学出版会、1987年、I章§4(pp.33-38)。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.2.3(p.124)。