→
戻る
証明:
ユークリッド空間R2上の点列の収束と座標ごとの収束の関係
[高木『解析概論』p.14:R2; 小平『解析入門I』§1.6-d(p.60) :R2上 ;吹田新保『理工系の微分積分学』p.155-6;
矢野『距離空間と位相構造』例1.9(p.12) :Rn; 志賀『位相への30講』第13講(pp.91-2):Rn;
神谷浦井『経済学のための数学入門』定理4.3.1(p.138) :n次元;杉浦『解析入門I』1章§4定理4.5-1(p.38);:n次元]
(設定) (R2,d) : R2にユークリッド距離を与えてつくったユークリッド空間
P : ユークリッド空間 (R2,d)上の点 ( x ,y )を表すとする。
{Pi}i∈N : ユークリッド空間 (R2,d)上の点列{P1 , P2 , P3 , …}で、
各点Piはふたつの実数の順序対[つまり座標]( xi , yi )を表すとする。
つまり点列{P1 , P2 , P3 , …}は、{ (x1 , y1) , (x2 , y2) , (x3 , y3) ,… }とも書ける。
{xi}i∈N : 点列{Pi}i∈Nの各点Pi( xi , yi )のxiだけを取り出して並べた数列{ x1 , x2, x3,… }
{yi}i∈N : 点列{Pi}i∈Nの各点Pi( xi , yi )のyiだけを取り出して並べた数列{ y1 , y2, y3,… }
(定理)以下の二つの命題は同値である。
命題1: 点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する。
つまり、
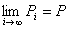
命題2: 数列{xi}i∈Nがxに収束し、かつ、数列{yi}i∈Nがyに収束する。

(
証明) A.予備的考察/B.命題1⇒命題2の証明/
C.命題2⇒命題1の証明(その1)/D.命題2⇒命題1の証明(その2)/E.命題2⇒命題1の証明(その3)
A.
予備的考察:ユークリッド距離の性質をここの文脈に適用
ユークリッド距離の性質1・性質2・性質3・性質4・性質5より、
点列{Pi}i∈Nの任意の各点Pi( xi , yi )と、点P( x ,y )との間のユークリッド距離
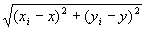
は、以下の不等式をいつでもみたす。
・任意のi∈Nにたいして、
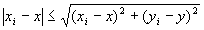 …(A-1)
…(A-1)
∵ユークリッド距離の性質1
・任意のi∈Nにたいして、
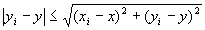 …(A-2)
…(A-2)
∵ユークリッド距離の性質2
・任意のi∈Nにたいして、
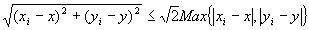 …(A-3)
…(A-3)
ただし、Max ( |xi−x| , | yi−y | )は、「|xi−x|と| yi−y |のうち、大きいほうの値」
つまり、(0-3)は、
(ケース1) |xi−x|≦| yi−y |となる点Pi (xi,yi)については、
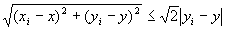 …(A-3-a)
…(A-3-a)
(ケース2) |xi−x|≧| yi−y |となる点Pi (xi,yi)については、
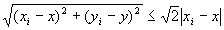 …(A-3-b)
…(A-3-b)
ということ。
・任意のi∈Nにたいして、
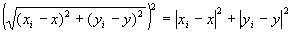 …(A-4)
…(A-4)
∵ユークリッド距離の性質4
・任意のi∈Nにたいして、
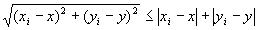 …(A-5)
…(A-5)
∵ユークリッド距離の性質5
→
先頭に戻る
B. 命題1⇒命題2の証明
[志賀『位相への30講』第13講(pp.91-2):Rnにおいて;矢野『距離空間と位相構造』例1.9(p.12); 吹田新保『理工系の微分積分学』pp..155-6;
杉浦『解析入門I』1章§4定理4.5-1(p.38):n次元; 神谷浦井『経済学のための数学入門』定理4.3.1(p.138) :n次元;]
以下、step1で、
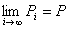 ⇒
⇒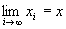
を示し、step2で、
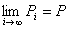 ⇒
⇒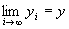
を示すことで、
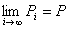 ⇒
⇒
を示す。
[stepI: 命題1⇒命題2前半]
(概略)
・任意のi∈Nにたいして
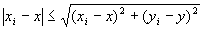 …(A-1)
…(A-1)
が成り立つが、
・命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」が成り立つならば、
点列の収束の定義より、
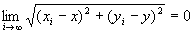
・よって、i→∞で、(A-1)右辺が0に収束するから、(A-1)左辺も0に収束。
(詳細)
命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」とは、
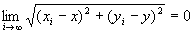
のこと、すなわち、
( ∀ε>0 ) (∃N∈N) (∀i∈N) ( i≧N⇒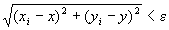 ) …(B-1)
) …(B-1)
のことであった(点列の収束の定義より)。
(A-1)より任意のi∈Nにたいして
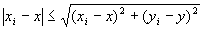
が成り立つので、
命題1すなわち(B-1)が成り立つならば、
( ∀ε>0 ) (∃N∈N) (∀i∈N) ( i≧N⇒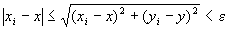 )
)
が成り立つ。
つまり、
命題1すなわち(B-1)が成り立つならば、
( ∀ε>0 ) (∃N∈N) (∀i∈N) ( i≧N⇒|xi−x|<ε) が成り立つ。
数列の収束・極限値の定義を用いて、このことを書きなおすと、
命題1すなわち(B-1)が成り立つならば、
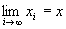
が成り立つ、となる。
[stepII: 命題1⇒命題2後半]
(要旨)
・任意のi∈Nにたいして
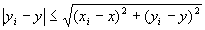 …(A-2)
…(A-2)
が成り立つが、
・命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」が成り立つならば、
点列の収束の定義より、
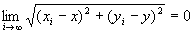
・よって、i→∞で、(A-2)右辺が0に収束するから、(A-2)左辺も0に収束。
(厳密には)
命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」とは、
( ∀ε>0 ) (∃N∈N) (∀i∈N) ( i≧N⇒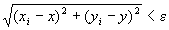 ) …(B-2)
) …(B-2)
のことであった。
(A-2)より任意のi∈Nにたいして
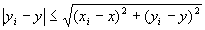
が成り立つので、
命題1すなわち(B-2)が成り立つならば、
( ∀ε>0 ) (∃N∈N) (∀i∈N) ( i≧N⇒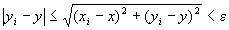 )
)
が成り立つ。
つまり、
命題1すなわち(B-2)が成り立つならば、
( ∀ε>0 ) (∃N∈N) (∀i∈N) ( i≧N⇒|yi−y|<ε) が成り立つ。
数列の収束・極限値の定義を用いて、このことを書きなおすと、
命題1すなわち(B-2)が成り立つならば、
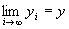
が成り立つ、となる。
C.
命題2⇒命題1の証明(その1)
[志賀『位相への30講』第13講(pp.91-2):Rnにおいて;矢野『距離空間と位相構造』例1.9(p.12);]
(概略)
・任意のi∈Nにたいして、
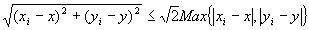 …(A-3)
…(A-3)
が成り立つ。
・命題2: が成り立つならば、
が成り立つならば、
i→∞で、(A-3)右辺が0に収束するから、(A-3)左辺も0に収束。
・(A-3)左辺の収束は、命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」の定義にほかならない。
(詳細)
Step1:点列の点を二つに分類
点列{Pi}i∈Nを構成する各点Pi (xi,yi)は、
・|xi−x|≦| yi−y |を満たす点Pi(xi,yi) であるか、
・|xi−x|>| yi−y |を満たす点Pi(xi,yi) であるか、
のいずれかである(両方であることもなければ、どちらでもないこともない)。
便宜上、
|xi−x|≦| yi−y |を満たす点Pi(xi,yi)の添数iをすべてあつめた集合を、Aで表し、
|xi−x|>| yi−y |を満たす点Pi(xi,yi)の添数iをすべてあつめた集合を、Bで表すことにする。
なお、
点列{Pi}i∈Nの添数iをすべてあつめた集合は、自然数全体の集合Nであったから、
A⊂N、 B⊂N、A∪B=N、A∩B=φである。
この添数の集合Aを用いて、
|xi−x|≦| yi−y |を満たす点Pi(xi,yi)のみを抜き出した「点列{Pi}i∈Nの部分列」を、{Pi}i∈Aで表し、
|xi−x|≦| yi−y |を満たす点Pi(xi,yi)のxiのみを抜き出した「数列{xi}i∈N の部分列」を、{xi}i∈Aで表し、
|xi−x|≦| yi−y |を満たす点Pi(xi,yi)のyiのみを抜き出した「数列{yi}i∈N の部分列」を、{yi}i∈Aで表すことにする。
また、この添数の集合Bを用いて、
|xi−x|>| yi−y |を満たす点Pi(xi,yi)のみを抜き出した「点列{Pi}i∈Nの部分列」を、{Pi}i∈Bで表し、
|xi−x|>| yi−y |を満たす点Pi(xi,yi)のxiのみを抜き出した「数列{xi}i∈N の部分列」を、{xi}i∈Bで表し、
|xi−x|>| yi−y |を満たす点Pi(xi,yi)のyiのみを抜き出した「数列{yi}i∈N の部分列」を、{yi}i∈Bで表すことにする。
Step2: 点列の点の分類の一方{Pi}i∈A、{xi}i∈A、{yi}i∈Aについて
ここでは、{Pi}i∈A、{xi}i∈A、{yi}i∈Aに限定して考える。
数列{xi}i∈N、数列{yi}i∈N について、
命題2:
がなりたつならば、数列{xi}i∈N,{yi}i∈Nの部分列である{xi}i∈A,{yi}i∈Aもそれぞれx,yに収束する(∵収束する数列の任意の部分列は収束する)
数列の極限の定義を用いて正確に言いなおすと、
「命題2が成り立つならば、
(∀ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒| xi −x|<ε) かつ (∀ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒| yi −y|<ε) 」
※ {Pi}i∈A、{xi}i∈A、{yi}i∈Aは、|xi−x|≦| yi−y |を満たす点Pi(xi,yi)ばかりを集めた点列・数列だったから、
「命題2が成り立つならば、
(∀ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒| xi −x|≦| yi−y |<ε) 」
といってもよい。
ここでさしあたり注目したいのは、
「命題2が成り立つならば、
(∀ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒| yi −y|<ε) 」…(C-1)
という点だけである。
(A-3-a)より、 |xi−x|≦| yi−y |となる任意の点Pi (xi,yi)については、
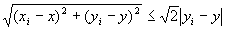
であったから、
|xi−x|≦| yi−y |を満たす点Pi(xi,yi)ばかりを集めた点列{Pi}i∈B・数列{xi}i∈B、{yi}i∈Bでは、
すべてのi∈Bについて、
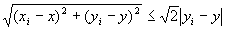
が満たされる。…(C-2)
(C-1) (C-2)を合せて考えると、
「命題2が成り立つならば、
(∀ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒| yi −y|<ε⇒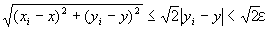 ) 」
) 」
となる。
上記について、要点以外を省略すると、
「命題2がなりたつならば、 (∀ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒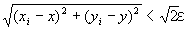 ) 」
) 」
となる。 また、これは、以下のようにいってもかわらない。
「命題2がなりたつならば、(∀√2・ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒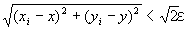 ) 」…(C-3)
) 」…(C-3)
Step3: 点列の点の分類の一方{Pi}i∈B、{xi}i∈B、{yi}i∈Bについて
ここでは、{Pi}i∈B、{xi}i∈B、{yi}i∈Bに限定して考える。
命題2:
がなりたつならば、その部分列である{xi}i∈B、{yi}i∈Bもそれぞれx,yに収束する(∵収束する数列の任意の部分列は収束する)
数列の極限の定義を用いて正確に言いなおすと、
「命題2が成り立つならば、
(∀ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒| xi −x|<ε) かつ (∀ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒| yi −y|<ε) 」
※ {Pi}i∈B、{xi}i∈B、{yi}i∈Bは、|xi−x|>| yi−y |を満たす点Pi(xi,yi)ばかりを集めた点列・数列だったから、
「命題2が成り立つならば、
(∀ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒| yi−y |<| xi −x|<ε) 」
といってもよい。
ここでさしあたり注目したいのは、
「命題2が成り立つならば、
(∀ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒| xi −x|<ε) 」…(C-4)
という点だけである。
(A-3-b)より、 |xi−x|≧| yi−y |となる任意の点Pi (xi,yi)については、
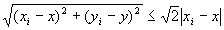
であったから、|xi−x|>| yi−y |を満たす点Pi(xi,yi)ばかりを集めた点列{Pi}i∈B・数列{xi}i∈B、{yi}i∈Bでは、
任意のi∈Bについて、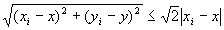 である。…(C-5)
である。…(C-5)
(C-4) (C-5)を合せて考えると、
「命題2が成り立つならば、
(∀ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒| xi −x|<ε⇒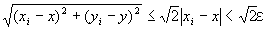 ) 」
) 」
となる。
上記について、要点以外を省略すると、
「命題2がなりたつならば、 (∀ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒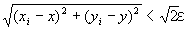 ) 」
) 」
となる。 また、これは、以下のようにいってもかわらない。
「命題2がなりたつならば、(∀√2・ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒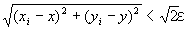 ) 」 …(C-6)
) 」 …(C-6)
Step5: 点列の点の各分類についての結果を統合する
ここまでの結果(C-3)(C-6)をあわせると、
「命題2がなりたつならば、
(∀√2・ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N1⇒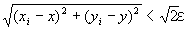 )
)
かつ (∀√2・ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N2⇒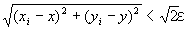 ) 」
) 」
すると、
N1とN2のうちおおきいほうか、それ以上の自然数をNで表すことにすると、
「命題2がなりたつならば、
(∀√2・ε>0) (∃N1∈N) (∀i∈A⊂N) ( i≧N≧N1⇒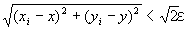 )
)
かつ (∀√2・ε>0) (∃N2∈N) (∀i∈B⊂N) ( i≧N≧N2⇒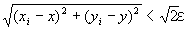 ) 」
) 」
である。すると、
「命題2がなりたつならば、
( ∀√2・ε>0 ) (∃N∈N) (∀i∈A∪B= N) ( i≧N⇒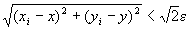 )
)
といえる。
つまり、
「命題2がなりたつならば、
( ∀ε' >0 ) (∃N∈N) (∀i∈N) ( i≧N⇒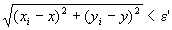 )
)
これは、
命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する
ということであった。∵ユークリッド平面上の点列の収束の定義
D.
命題2⇒命題1の証明(その2) [杉浦『解析入門I』1章§4定理4.5-1(p.38):n次元ユークリッド空間において;]
(概略)
・任意のi∈Nにたいして、
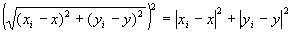 …(A-4)
…(A-4)
が成り立つ。
・命題2: が成り立つならば、
が成り立つならば、
i→∞で、(A-4)右辺が0に収束するから、(A-4)左辺も0に収束。
・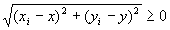 だから、
だから、
(A-4)左辺が0に収束するならば、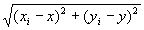 も0に収束する。
も0に収束する。
これは、命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」の定義にほかならない。
(詳細)
step1:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、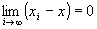 かつ
かつ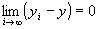
なぜなら、 かつ
かつ が成り立つならば、
が成り立つならば、
・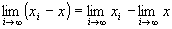 ∵極限値の和の演算則
∵極限値の和の演算則
=x−x=0 ∵ の仮定下で考えているから。
の仮定下で考えているから。
かつ
・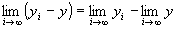 ∵極限値の和の演算則
∵極限値の和の演算則
=y−y=0 ∵ の仮定下で考えているから。
の仮定下で考えているから。
Step2:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、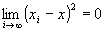 かつ
かつ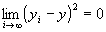
なぜなら、
 かつ
かつ が成り立つならば、
が成り立つならば、
step1より、 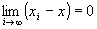 かつ
かつ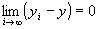 だから、
だから、
・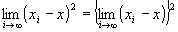 ∵極限値の積の演算則
∵極限値の積の演算則
=0 かつ
・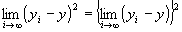 ∵極限値の積の演算則
∵極限値の積の演算則
=0
Step3:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、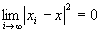 かつ
かつ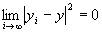
なぜなら、
・step2より、 かつ
かつ が成り立つならば、
が成り立つならば、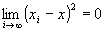 かつ
かつ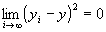
・絶対値の性質 より、(xi-x)2=|xi-x|2
ゆえに、
 かつ
かつ が成り立つならば、
が成り立つならば、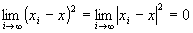 かつ
かつ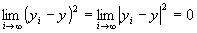
Step4:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、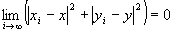
なぜなら、
step3より、 かつ
かつ が成り立つならば、
が成り立つならば、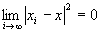 かつ
かつ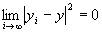 だから、
だから、
 かつ
かつ が成り立つならば、
が成り立つならば、
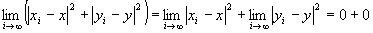 ∵極限値の和の演算則
∵極限値の和の演算則
Step5:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、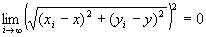
なぜなら、
(A-4)より、いつでも、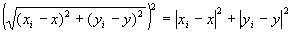 だから、
だから、
step4より、 かつ
かつ が成り立つならば、
が成り立つならば、
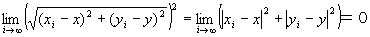
Step6:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、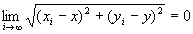
なぜなら、
・いつでも、 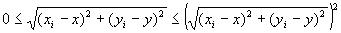
・step5より、 かつ
かつ が成り立つならば、
が成り立つならば、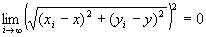
以上2点から、
 かつ
かつ が成り立つならば、
が成り立つならば、
いわゆるはさみうちの原理が適用されて、
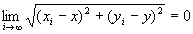
Step7:
命題2: かつ
かつ が成り立つならば、命題1:
が成り立つならば、命題1: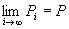
なぜなら、
・step6より、命題2: かつ
かつ が成り立つならば、
が成り立つならば、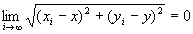
・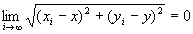
は、命題1「点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」の定義
したがって、
命題2: かつ
かつ が成り立つならば、
が成り立つならば、
命題1: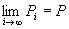
といってよい。
E. 命題2⇒命題1の証明(その3)
[神谷浦井『経済学のための数学入門』定理4.3.1(p.138) :n次元ユークリッド空間において;
吹田新保『理工系の微分積分学』p.155-6 ]
(概略)
・任意のi∈Nにたいして、
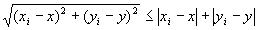 …(A-5)
…(A-5)
が成り立つ。
・命題2: が成り立つならば、
が成り立つならば、
i→∞で、(A-5)右辺が0に収束するから、(A-5)左辺も0に収束。
これは、命題1:点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」の定義にほかならない。
(詳細)
step1:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、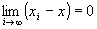 かつ
かつ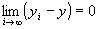 …(E-1)
…(E-1)
なぜなら、 かつ
かつ が成り立つならば、
が成り立つならば、
・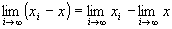 ∵極限値の和の演算則
∵極限値の和の演算則
=x−x=0 ∵ の仮定下で考えているから。
の仮定下で考えているから。
かつ
・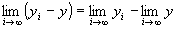 ∵極限値の和の演算則
∵極限値の和の演算則
=y−y=0 ∵ の仮定下で考えているから。
の仮定下で考えているから。
Step2:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、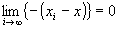 かつ
かつ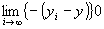
なぜなら、
・ かつ
かつ が成り立つならば、
が成り立つならば、
step1より、 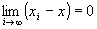 かつ
かつ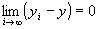 だから、
だから、
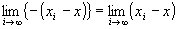 ∵極限値の演算則
∵極限値の演算則
=0
かつ
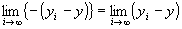 ∵極限値の演算則
∵極限値の演算則
=0
Step3:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、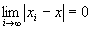 かつ
かつ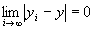
なぜなら、
 かつ
かつ が成り立つならば、
が成り立つならば、
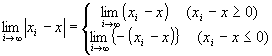 ∵絶対値の定義
∵絶対値の定義
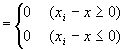 ∵step1,step2
∵step1,step2
=0
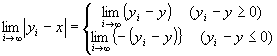 ∵絶対値の定義
∵絶対値の定義
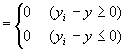 ∵step1,step2
∵step1,step2
=0
Step4:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、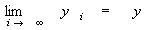
なぜなら、
 かつ
かつ が成り立つならば、
が成り立つならば、
step3より、 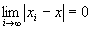 かつ
かつ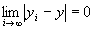 だから、
だから、
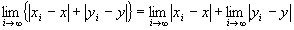 ∵極限値の和の演算則
∵極限値の和の演算則
=0+0=0
Step5:
命題2: かつ
かつ が成り立つならば、
が成り立つならば、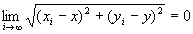
なぜなら、
・(A-5)より、いつでも、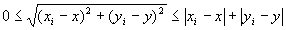
・step4より、 かつ
かつ が成り立つならば、
が成り立つならば、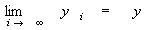
以上2点から、
 かつ
かつ が成り立つならば、
が成り立つならば、
いわゆるはさみうちの原理が適用されて、
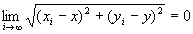
Step6:
命題2: かつ
かつ が成り立つならば、命題1:
が成り立つならば、命題1: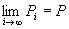
なぜなら、
・step5より、命題2: かつ
かつ が成り立つならば、
が成り立つならば、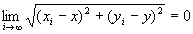
・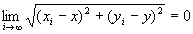
は、命題1「点列{Pi}i∈N={ (x1 , y1), (x2 , y2) , (x3 , y3) ,… }が、点P=(x,y)へ収束する」の定義
したがって、
命題2: かつ
かつ が成り立つならば、
が成り立つならば、
命題1: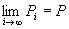
といってよい。
→
戻る
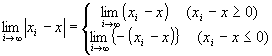 ∵絶対値の定義
∵絶対値の定義 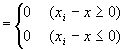 ∵step1,step2
∵step1,step2 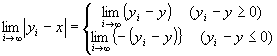 ∵絶対値の定義
∵絶対値の定義 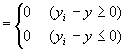 ∵step1,step2
∵step1,step2