「A⇒B」の読み
・論理記号「A⇒B」は、
含意の命題
「命題Aならば命題B」「 AはBの十分条件 」「BはAの必要条件」
" A only if B", " B if A " ," A implies B ","B is implied by A"
を表す。
※記号「A⇒B」の代わりに、「A⊃B」を用いるテキストもある。
[→岡田『経済学・経営学のための数学』]
「A⇒B」の真理値表
・含意の命題「命題Aならば命題B」(論理記号では「A⇒B」)の真偽は、
次の真理値表により、命題A,命題Bの真偽から、定められる。 |
|
|
A
|
B
|
A⇒B |
| 真 |
真 |
真 |
| 真 |
偽 |
偽 |
| 偽 |
真 |
真 |
| 偽 |
偽 |
真 |
|
※真/偽は、その命題が「成り立つ/たない」ぐらいにとる。
|
※真理値表をみるとわかるように、A⇒B は、「 AならばB 」という語感と異なって、Aが成り立たないときは、いつでも、A ⇒ B が成立する(真である)ように定義されている。
つまり、「A⇒B 」は、実は、( ¬A ) ∨ B 「Aが成り立たない、または、Bがなりたつ」である。
※背理法による証明は、このことを根拠とする。 [中内『ろんりの練習帳』65]
※「いかなる集合Aに対しても、φ⊂A」は、このことを根拠とする。
「A⇒B」の歴史
・井関『集合と論理』(p.16:脚注1)によれば、このように「ならば」の定義を定式化したのは、米国のパース C.Peirce (1839-1914)。
・中谷『論理』2.1 条件文 (2.2) (p.30)は、このような「ならば」の定義は、古代ギリシアのメガラ-ストア学派によって開拓されたと指摘。
含意の命題「AならばB」A⇒Bの言い換え
・下記の表現は、同じこと。互いに言い換え可。
(表現1) 「AならばB」 論理記号で表すと 「 A⇒B 」
(表現2) 「Bでないならば、Aでない 」 論理記号で表すと 「 ¬B⇒¬A 」
(表現3) 「Aでない、または、B」 論理記号で表すと 「 ( ¬A ) ∨ B 」
(表現4) 「『Aかつ《Bでない》』ということはない」 論理記号で表すと 「 ¬ ( A ∧ (¬B) )」
・どうして、(表現1)と(表現2)は言い換え可? 対偶だから。
・どうして、(表現1)と(表現3)は言い換え可?
真理値表を書くと(→右表)、
(表現1)と(表現3)の真偽が一致するとわかるので。
|
A
|
B
|
A⇒B |
¬A
| ( ¬A ) ∨ B |
| 真 |
真 |
真 |
偽 | 真 |
| 真 |
偽 |
偽 |
偽 | 偽 |
| 偽 |
真 |
真 |
真 | 真 |
| 偽 |
偽 |
真 |
真 | 真 |
|
・どうして、(表現3)と(表現4)は言い換え可? ¬(A∧B) と (¬A)∨(¬B) とは言い換え可能 より。
|
|
|
|
|
・(表現1)と(表現2)の言い換えについて言及している文献
・中内『ろんりの練習帳』定理1.9.2(p.48);1.11(2)(p.65)
・中谷『論理』2.1条件文-B.逆裏対偶 (2.4) (p.33):真理値表をつくればすぐ分かると指摘。
・井関『集合と論理』1.4恒真式 例2(1) (p.21):真理値表をつかった説明。式の変形をつかった説明。
・(表現1)と(表現3)の言い換えについて言及している文献
・中内『ろんりの練習帳』定義1.8.1(p.43):(表現3)(表現4)を(表現1)の定義としている。
・中谷『論理』2.1条件文-A.条件文の意味 (2.2) (p.30):(表現3)を(表現1)の定義としている。
・井関『集合と論理』1.4恒真式 (4.3) (p.18)
・野矢『論理学』問題17(1) (p.44)
・(表現1)と(表現4)の言い換えについて言及している文献
・中内『ろんりの練習帳』定義1.8.1(p.43):(表現3)(表現4)を(表現1)の定義としている。
・中谷『論理』 2.1 条件文-A.条件文の意味(2.1)(p.29):(表現4)を(表現1)の定義としている。
・井関『集合と論理』1.4恒真式 (4.3) (p.18)
・(表現3)と(表現4)の言い換えについて言及している文献
・中谷『論理』 2.1 条件文-A.条件文の意味(2.1)(pp.29-30):二重否定とモルガン則を使うと指摘。
|
|
|
|
|
|
含意の命題「AならばB」A⇒Bの具体例
【例】 20xx年某国で原発事故発生、不安にかられた某国国民の世論に押されて、某国政府は国内すべての原発の稼働停止に追い込まれた。
1年後、某国首相は、「●●原発が安全であるならば、●●原発を再稼働する」と宣言、
数週間後、某国首相は、実際に●●原発再稼働を実行した。
ところが…
「●●原発が安全」ではないことが、最悪のかたちで露呈!
「安全でないのに再稼働しただろ! この嘘つき! デマ野郎!」と罵る世論。
これに対し、首相は、胸を張って断言。「ワタクシは嘘をついておりません。」
[問1] 首相は嘘をついたのだろうか?
[問2] 首相が「●●原発が安全であるならば、●●原発を再稼働する」という宣言に背いたと言えるのは、いかなる行動を首相がとった場合だろうか?
[問3] 「●●原発が安全であるならば、●●原発を再稼働する」という宣言を他の表現に言い換えたら、どうなるだろうか?
[答1] 首相は嘘をついていない。
「●●原発が安全であるならば、●●原発を再稼働する」の真理値表を書き出してみよう。
|
| ●●原発が安全である |
●●原発を再稼働する |
「●●原発が安全であるならば、●●原発を再稼働する」 |
|
| 真 |
真 |
真 |
←1行目 |
| 真 |
偽 |
偽 |
←2行目 |
| 偽 |
真 |
真 |
←3行目 |
| 偽 |
偽 |
真 |
←4行目 |
|
|
・真理値表から明らかなように、
「●●原発が安全」でない場合、「●●原発を再稼働」しても、「●●原発が安全であるならば、●●原発を再稼働する」は真。
だから、
首相が「●●原発が安全」でない場合に、「●●原発を再稼働」したところで、自らの宣言に背いたことにはならない。
・ちなみに、「●●原発が安全」でない場合に、「●●原発を再稼働」しないとしても、「●●原発が安全であるならば、●●原発を再稼働する」は真。
・そもそも、「●●原発が安全であるならば、●●原発を再稼働する」という宣言は、
「●●原発が安全」でない場合の「●●原発再稼働」の有無について、何ら言及するものでないのだ。
[問2]
・真理値表をみると、「●●原発が安全であるならば、●●原発を再稼働する」という宣言が偽になりうるのは、
「●●原発が安全」であるのに、「●●原発を再稼働」しないケースだけ。
・だから、首相が、「●●原発が安全であるならば、●●原発を再稼働する」という宣言に背いたといえるのは、
「●●原発が安全」であるのに、「●●原発を再稼働」しなかった場合だけである。
・つまり、「●●原発が安全であるならば、●●原発を再稼働する」という宣言は、
「●●原発が安全であるのに、●●原発を再稼働しない」という選択の否定を表明したただけだ
ということになる。
[問3] 「●●原発が安全であるならば、●●原発を再稼働する」の言い換え
(表現4) 「『《●●原発は安全》かつ《●●原発を再稼働しない》』ということはない」
つまり、「●●原発が安全であるのに、●●原発を再稼働しない」という選択肢を否定。
(表現2) 「●●原発を再稼働しないならば、●●原発は安全でない 」
(表現3) 「●●原発は安全でない、または、●●原発を再稼働する」
つまり、 ●●原発は、安全でない、か、再稼働するか、のいずれか一方、あるいは、その両方に該当する。
【例】 A「x >2」⇒ B「 x >1」
※真理値表:真/偽は、その命題が「成り立つ/たない」ぐらいにとる。
| A | B | A⇒B |
├───┼───┼─────┤
2 <x | 真 | 真 | 真 | ←1行目
| 真 | 偽 | 偽 | ←2行目
1 <x ≦2 | 偽 | 真 | 真 | ←3行目
x ≦1 | 偽 | 偽 | 真 | ←4行目
「A:x >2 ⇒ B: x >1」が偽となる2行目はありえないので、
「A:x >2 ⇒ B: x >1」は常に真と判断できる。
Aが偽である場合(x≦2)のBの真偽は、
「A:x >2 ⇒ B: x >1」の真偽に影響を与えていないことに注意。
|
|
「A⇒B」と十分条件・必要条件との関連
「A ⇒ B」という命題が成り立っている(真である)と仮定するならば、
その仮定のもとでは、
「A ⇒ B」が偽となる、真理値表2行目のケースは、そもそもありえないので、
真理表2行目は削除して考えて良いことになる。
つまり、
「A ⇒ B」という命題が成り立っている(真である)
との仮定のもとでの真理値表は、
|
A
|
B
|
A⇒B |
|
| 真 |
真 |
真 | ←1行目
|
| 真 |
偽 |
偽 | ←2行目 |
| 偽 |
真 |
真 | ←3行目 |
| 偽 |
偽 |
真 | ←4行目 |
|
|
|
A
|
B
|
A⇒B |
|
| 真 |
真 |
真 | ←1行目
|
| 偽 |
真 |
真 | ←3行目 |
| 偽 |
偽 |
真 | ←4行目 |
|
|
同じことをベン図でも考えてみよう。
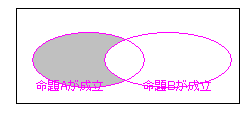
「A ⇒ B」という命題が成立しないのは、上のベン図のグレーの部分(真理値表2行目)、
「A ⇒ B」という命題が成立するのは、それ以外のすべての領域(真理値表1・3・4行目)である。
だから、
「A ⇒ B」という命題が成り立っている(真である) (真理値表1・3・4行目)と仮定するならば、
その仮定のもとでは、
上のベン図のグレーの部分(真理値表2行目)はそもそもありえないということになるので、
グレーの部分を削除したベン図で考えるのが妥当となる。
グレーの部分が存在しえないようにベン図を書きなおすと、
「Aが成立するケース」⊂「Bが成立するケース」とせざるをえないので、
教科書等でよく見かける下の図になる。
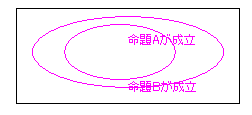
以上からわかるように、
「A ⇒ B」という命題が成り立っている(真である)との仮定のもとでは、
Aが成り立つ(真である)ならば、つねに、Bも成り立つが(真理値表1行目)、
Bが成り立つ(真である)からといって、Aがなりたつとも限らない(真理値表2-3行目)
ということになる。
「A ⇒ B」という命題が成り立っている(真である)ならば、
AをBの「十分条件」、BをAの「必要条件」と呼ぶのは、
このような意味においてである。
「A⇒B」の証明
|
中学以来おぼえさせられてきた「A ⇒ B」が成立する(真である)ことの証明方法は、
なぜ妥当性をもつのか。
(1) Aの真偽の仮定から出発して、その仮定下でのBの真偽を確認して、「A⇒B」の真偽をテストする証明方法
Aが成立する(真である)という仮定のもとで、Bが成立する(真である)かどうかの検討はするが、
Aが成立しない(偽である)という仮定のもとで、Bが成立する(真である)や否やの検討はそもそもやらない。
なぜだろう?
これは、「A ⇒ B」という命題の真偽を、上の真理値表で定義したことによる。
つまり、
Aが偽である場合、つまり、真理値表の3〜4行目に当る場合は
「A ⇒ B」という命題はつねに真とされるから、このケースの検討は不要であるが、
| A | B | A⇒B |
├───┼───┼─────┤
| 偽 | 真 | 真 | ←3行目
| 偽 | 偽 | 真 | ←4行目
Aが真である場合、つまり、真理値表の1・2行目のどちらかにあたる場合は、
そのどちらかに当るかによって、「A ⇒ B」という命題の真偽が変わってくるゆえ、
このケースでの検討が不可欠となる。
| A | B | A⇒B |
├───┼───┼─────┤
| 真 | 真 | 真 | ←1行目
| 真 | 偽 | 偽 | ←2行目
ここで、Aが真であると仮定すると常にBが真(1行目のケース)とならざるをえず、
Bが偽である2行目のケースがありえないことを示せれば、
「A ⇒ B」が成立する(真である)と証明できたことになる。
(2) Bの真偽の仮定から出発して、その仮定下でのAの真偽を確認して、「A⇒B」の真偽をテストする証明方法
対偶「 ¬B⇒¬A 」が成り立つ(真である)ことを示すことで、「A ⇒ B」の成立を示す証明法もやらされたが、
あのやり方が妥当であるのも、「A ⇒ B」という命題の真偽を、上の真理値表で定義したことによる。
まず、Bが成り立つ(真である)という仮定から出発したのでは、意味がない。
Bが成り立つ(真である)という仮定をおくことは、真理値表の1行目と3行目だけを考えるということになるが、
このときは、Aの真偽(成立/不成立)に関わりなく、「A ⇒ B」はどうせ真とされるから、
このような検討をわざわざ行う必要はない。
| A | B | A⇒B |
├───┼───┼─────┤
| 真 | 真 | 真 | ←1行目
| 偽 | 真 | 真 | ←3行目
しかし、Bが成り立たない(偽である)との仮定のもとでのAの真偽(成立/不成立)の検討は、
「A ⇒ B」の真偽のテストにおいて決定的である。
Bが成り立たない(偽である)との仮定のもとで検討するということは、
真理値表の2行目と4行目のみを見ていることになる。
Bが成り立たない(偽である)との仮定のもとでのAの真偽(成立/不成立)は、
「A ⇒ B」という命題の偽真を分けている。
| A | B | A⇒B |
├───┼───┼─────┤
| 真 | 偽 | 偽 | ←2行目
| 偽 | 偽 | 真 | ←4行目
ここで、
Bが成り立たない(偽である)と仮定すれば、Aも偽とならざるをえず(4行目のケース)、Aが真となる2行目のケースがありえない
ということを示せれば、
「A ⇒ B」が成立する(真である)と証明できたことになる。
※
「A ⇒ B」が唯一偽となる2行目が決定的であるゆえ、
(1)の証明でも(2)の証明でも、必ずここをからめて検討している。
(3) 背理法
「A ⇒ B」は、
「Aが成り立たない、または、Bが成り立つ」
論理記号で書くと、「( ¬A ) ∨ B」
であった。
「Aが成り立たない、または、Bが成り立つ」( ¬A ) ∨ B
は、
「Aが成り立たない、または、『Bが成り立たない』が成り立たない」
( ¬A ) ∨ (¬(¬B) )
と言いかえられ、 (∵2重否定)
「Aが成り立たない、または、『Bが成り立たない』が成り立たない」
( ¬A ) ∨ (¬(¬B) )
は、
「『Aが成り立ち、かつ、Bが成り立たない』が成り立たない」
¬ ( A ∧ (¬B) )
と言いかえられる(∵)
だから、結局、「A ⇒ B」は、
「『Aが成り立ち、かつ、Bが成り立たない』が成り立たない」
¬ ( A ∧ (¬B) )
である。
背理法は、この
「『Aが成り立ち、かつ、Bが成り立たない』が成り立たない」
¬ ( A ∧ (¬B) )
なる命題が成り立つことを示すのが、背理法である。
※背理法を認めない流派もある(直観主義)。 |
→トピック一覧:論理記号
→総目次
[文献]
中内『ろんりの練習帳』64-66;
|
関連事項
・「ならば」の否定 ¬(⇒)
・「ならば」を繰り返す命題、「ならば」の全称/存在命題
・命題関数P(x)⇒Q(x)の真理集合/述語・命題関数の普遍量化 ∀x
(P(x)⇒Q(x))の集合表現

