→戻る
定理:k次関数の微分 [kが整数である場合]
任意の整数kにたいして、( x k ) ' = kxk-1
※ kが実数全体の場合は、x>0でのみ定義される。
kが分数(1/q)の場合、xのq乗根を考えなければならなくなることを、想起せよ。 [基礎解析p.43]
【文献】
・吹田・新保『理工系の微分積分学』p.37.
・高橋『経済学とファイナンスのための数学』p.50
・『微分積分』pp.49-68;55
→戻る
証明1 : 数学的帰納法による証明
[文献]『微分積分』pp.49-68;55
( x k ) ' = kxk-1 …① の成り立つことを数学的帰納法で証明する。
(1) kが正の整数のとき
(i) k =1のとき、 ①の左辺=( x1) ' =1 ←要証明
①の右辺=1。 ゆえに、①は成立。
(ii) k = n のときに、①が成り立つと仮定すると、 (x n ) ' = n xn-1 …②
|
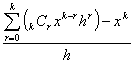 ∵二項定理
∵二項定理