Anhysteretic remanent magnetization of single-domain grains: A model with Neel's thermal activation theory
The ARM model using the Preisach diagram is applicable only to magnetically interacting SD grains. For noninteracting SD grains, ARM intensity is saturated even for a tiny DC magnetic field \(H_D\). The problem of infinite ARM susceptibility, i.e. \(\partial ARM/\partial H_D = \infty\), was solved by the model of Jaep (1969) which used Neel's thermal activation theory.
Theory of ARM acquisition under thermal activation
Consider an ensemble of \(N\) SD grains of magnetite whose easy axises are uniformly aligned. Now an alternating field of square wave is applied along the easy axis and a small DC field \(H_D\) is superposed.
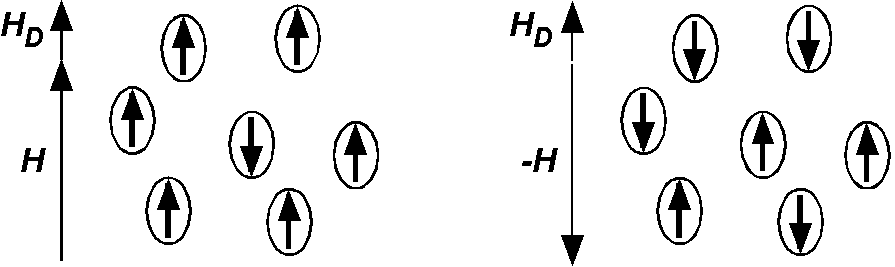
Taking the \(H_D\) direction as positive, numbers of positive and negative magnetizations are denoted by \(N_1\) and \(N_2\), respectively (\(N = N_1 + N_2\)). During the half cycle in which a positive peak field \(H\) is applied (left-hand figure), it is considered that the rotation of the magnetization to the \(-H\) direction rarely occurs. Hence, \begin{equation} \frac{dN_1}{dt} = \frac{1}{\tau_+}N_2, \label{eq01} \end{equation} where \(\tau_+\) is the relaxation time for the rotation from \(-H\) to \(H\) directions. Hereafter, normalized magnetization \(p\) is introduced as, \begin{equation} p = \frac{N_1 - N_2}{N}. \label{eq02} \end{equation} Using (1), and noting that \(dN_1/dt = -dN_2/dt\) and \(p = 1 - 2N_2/N\), \[ \frac{dp}{dt} = \frac{1}{N}\left(\frac{dN_1}{dt} - \frac{dN_2}{dt}\right) = \frac{2}{N}\frac{dN_1}{dt} = \frac{1}{\tau_+}\frac{2}{N}N_2 = \frac{1-p}{\tau_+}. \] Integrating this equation, \begin{align*} -\frac{dp}{1-p} & = -\frac{dt}{\tau_+}, \\ \log(1-p) & = -t/\tau_+ + C, \\ p & = 1 - Ke^{-t/\tau_+}, \end{align*} where \(C\) and \(K\) are constants of integration. Denoting \(p = p_0\) at \(t = 0\), \begin{equation} p = 1 - (1 - p_0)e^{-t/\tau_+}. \label{eq03} \end{equation} During the half cycle of a negative peak field \(-H\) (right-hand figure), \begin{equation} \frac{dN_2}{dt} = \frac{1}{\tau_-}N_1. \label{eq04} \end{equation} where \(\tau_-\) is the relaxation time for the rotation from \(H\) to \(-H\) directions. Similarly, \begin{align*} \frac{dp}{dt} & = \frac{1}{N}\left(\frac{dN_1}{dt} - \frac{dN_2}{dt}\right) = -\frac{2}{N}\frac{dN_2}{dt} = -\frac{1}{\tau_-}\frac{2}{N}N_1 = -\frac{1+p}{\tau_-}, \\ \frac{dp}{1+p} & = -\frac{dt}{\tau_-}. \end{align*} Integrating this with \(p=p_0\) at \(t=0\), we obtain, \begin{equation} p = -1 + (1 + p_0)e^{-t/\tau_-}. \label{eq05} \end{equation}
Now the peak field of the alternating field is gradually decreased to zero while \(H_D\) is kept applied (figure below).
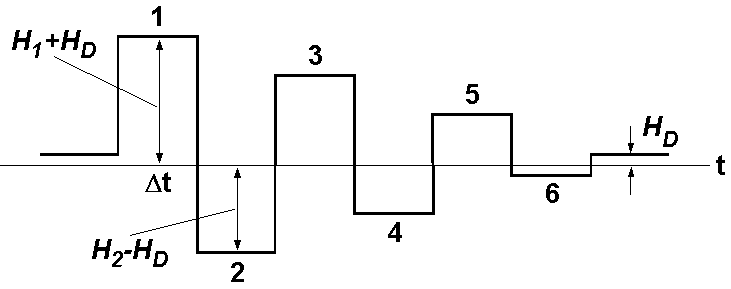
Let \(n\) be an odd number and the \(n\)th and \(n\)+1th peak fields are denoted by \(H_n\) and \(-H_{n+1}\), respectively. Equations of \(p_n\) and \(p_{n+1}\) for each half cycle are (3) and (5), respectively. The relaxation times \(\tau_+\) and \(\tau_-\) are those of "\(\tau_{21}\)" appeared in the previous pages, in which \(H\) is replaced by \(H_n+H_D\) and \(H_{n+1}-H_D\), respectively. Hence, equations governing the ARM acquisition model are as the followings, where \(A\) = 109 s-1. \begin{eqnarray} p_n & = & 1 - (1 - p_{n-1})e^{-\Delta t/\tau_n}, \label{eq06} \\ \tau_n & = & \frac{1}{A}\exp\left[\frac{\mu_0 VM_s H_K}{2kT}\left(1-\frac{H_n+H_D}{H_K}\right)^2\right], \label{eq07} \\ p_{n+1} & = & -1 + (1 + p_n)e^{-\Delta t/\tau_{n+1}}, \label{eq08} \\ \tau_{n+1} & = & \frac{1}{A}\exp\left[\frac{\mu_0 VM_s H_K}{2kT}\left(1-\frac{H_{n+1}-H_D}{H_K}\right)^2\right]. \label{eq09} \end{eqnarray}
Examples of simulation
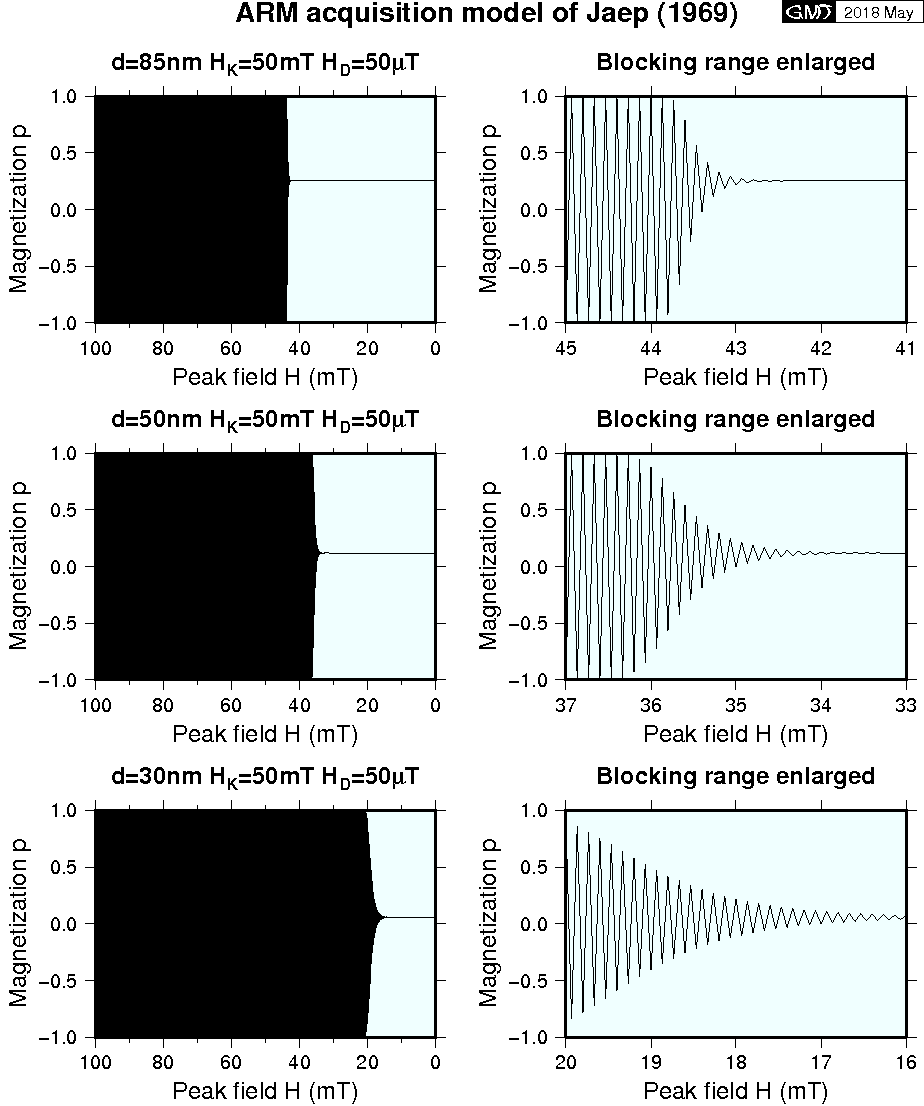
Simulation was carried out using equations (6) ~ (9), in which 50 Hz AC field with a peak field of 100 mT was decreased to zero in 30 s. Figures below show representative cases of ARM blocking for three grain diameters \(d\) = 85 nm (top figure), 50 nm (middle), and 30 nm (bottom) while micro coercivity \(H_K\) = 50 mT and the DC field \(H_D\) = 0.05 mT (50 μT) were kept the same. In the figure, it is seen that the blocking field, denoted by \(H_B\), is always smaller than \(H_K\) and this is due to input of thermal energy even at the room temperature. For the same reason, \(H_B\) is smaller and the range of \(H_B\) is wider tor the smaller grain. Blocked \(p\) is also smaller for the smaller grain.
Theoretical equation of the blocked \(p\)
Jaep (1969) also suggested that theoretical expression of ARM intensity can be obtained by setting \(p_{n-1} = p_{n+1}\), as the followings. Rewriting (6) as, \[ 1 - p_n = (1 - p_{n-1})e^{-\Delta t/\tau_n}, \] and multiplying both sides of (8) by \(e^{\Delta t/\tau_{n+1}}\), \[ 1 + p_n = (1 + p_{n+1})e^{\Delta t/\tau_{n+1}}. \] Adding the two equations and denoting \(p=p_{n-1}=p_{n+1}\), \[ 2 = (1 - p)e^{-\Delta t/\tau_n} + (1 + p)e^{\Delta t/\tau_{n+1}}. \] At the blocking, \(\Delta t/\tau_n, \Delta t/\tau_{n+1} \ll 1\), and hence using the approximation formula, \(e^x \approx 1+x\) (\(|x| \ll 1\)), \[ 2 = (1 - p)(1 - \Delta t/\tau_n) + (1 + p)(1 + \Delta t/\tau_{n+1}), \] and we obtain, \[ p = \frac{\Delta t/\tau_n - \Delta t/\tau_{n+1}}{\Delta t/\tau_n + \Delta t/\tau_{n+1}} = \frac{\tau_{n+1} - \tau_n}{\tau_{n+1} + \tau_n}. \] Substituting (7) and (9) to this equation, \[ p = \frac{\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H_D}{H_K}-\frac{H_{n+1}}{H_K}\right)^2\right] - \exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H_D}{H_K}-\frac{H_n}{H_K}\right)^2\right]} {\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1+\frac{H_D}{H_K}-\frac{H_{n+1}}{H_K}\right)^2\right] + \exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H_D}{H_K}-\frac{H_n}{H_K}\right)^2\right]}. \] Approximating the peak fields as \(H_{n+1} \approx H_n = H_B\), \(p\) is simplified to, \begin{eqnarray} p &=& \frac{\exp\left[\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right] - \exp\left[-\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right]} {\exp\left[\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right] + \exp\left[-\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right]}, \nonumber \\ &=& \tanh\left[\frac{\mu_0VM_sH_D}{kT}\left(1-\frac{H_B}{H_K}\right)\right]. \label{eq10} \end{eqnarray} The blocking field \(H_B\) is determined by setting the next relaxation time \(\tau_B\) to be 1 s, \begin{equation} \tau_{n+1} \approx \tau_n = \tau_B= \frac{1}{A}\exp\left[\frac{\mu_0VM_sH_K}{2kT}\left(1-\frac{H_B}{H_K}\right)^2\right] = 1. \label{eq11} \end{equation}
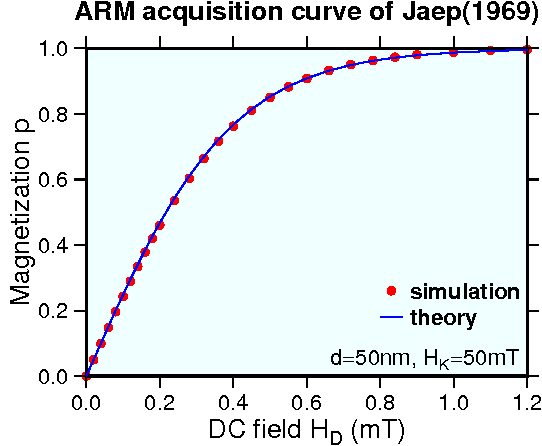
Right figure shows excellent agreement of the ARM acquisition curves between the simulation (red circle) and theory (blue line) for the case of \(d\) = 50 nm and \(H_K\) = 50 mT. However, the model's ARM susceptibility \(\partial p/\partial H_D\) is much larger than experimental observations even if considering the fact that the model is for the uniformly aligned SD grains not for those of random orientation. The discrepancy of the model and observations is caused by the strong magnetic interaction in ARM. Effect of magnetic interaction is stronger in ARM than TRM. This is because ARM blocking occurs at the room temperature in which the interaction field is large due to the large spontaneous magnetization \(M_s\) while TRM blocking occurs with small \(M_s\) at high temperatures. Nevertheless, Jaep's ARM model is superior to the Preisach model because the former gives a finite ARM susceptibility for noninteracting SD grains.
Jaep (1971) presented another ARM model based on the Neel's thermal activation theory, in which SD grains are magnetically interacting. Based on this updated ARM model, Tanaka (1999) discussed the similarity of ARM and TRM in relation to the ARM correction used in the Shaw paleointensity method.
References:
- Jaep, W. F., Anhysteretic magnetization of an assembly of single-domain particles, J. Appl. Phys., 40, 1297-1298, 1969.
- Jaep, W. F., Role of interactions in magnetic tapes, J. Appl. Phys., 42, 2790-2794, 1971.
- Tanaka, H., Theoretical background of ARM correction in the Shaw palaeointensity method, Geophys. J. Int., 137, 261-265, 1999. (→ doi:10.1046/j.1365-246X.1999.00783.x)