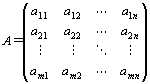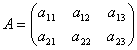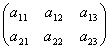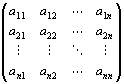|
定義 1 |
「 m行n列行列
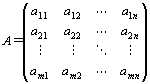
の小行列・部分行列」
とは、
Aのm個の行から選んだs個の行{第i1行, 第i2行,…第is行}
ただし、1≦i1<i2<…<is≦ m(トビがあってよい)
Aのn個の列から選んだt個の列{第j1列, 第j2列,…第jt列}
ただし、1≦j1<j2<…<jt≦n(トビがあってよい)
が交差する成分を並べたs行t列行列

のこと。 |
※ 関連事項:正方小行列/小行列式
[文献-全般]
・『岩波数学辞典』84行列式D (p.224);
[文献-線型代数]
・佐武『線型代数学』Ⅲ§4 (p.106:r次小行列式)
・草場『線形代数』2.12定義2.4(p.66);
・永田『理系のための線型代数の基礎』2.4(p.73):小行列式;
[文献-解析]
*松坂『解析入門4』16.2-E(p.51)フォーマルな定式化。
[文献-数理経済]
・西村『経済数学早わかり』2章§2.3(pp.58-61). k次小行列、5.1(p.86)
*二階堂『経済のための線型代数』I§4-6(p.46)。正方行列でなくてもよい。特に正方小行列については、行列式が定義され、これを小行列式という。 |
|
例 |
2行3列の行列
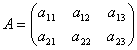
の小行列・部分行列は、
以下の21通り。[→二階堂『経済のための線型代数』I§4-6例6(pp.46-7)。]
(ex1-1) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列{第1列, 第2列,第3列}全てを選択した小行列
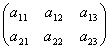
(ex 1-2) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列から{第1列, 第2列}を選択・第3列を排除した小行列
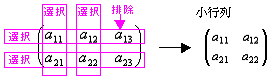
(ex 1-3) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列から{第1列, 第3列}を選択・第2列を排除した小行列
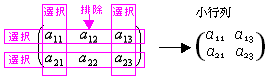
(ex 1-4) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列から{第2列, 第3列}を選択・第1列を排除した小行列
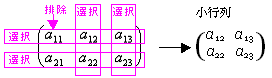
(ex 1-5) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列から{第1列}を選択・{第2列,第3列}を排除した小行列
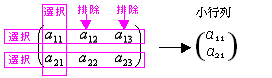
(ex 1-6) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列から{第2列}を選択・{第1列,第3列}を排除した小行列
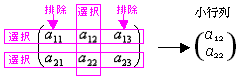
(ex 1-7) Aの2個の行{第1行, 第2行}全てを選択、Aの3個の列から{第3列}を選択・{第1列,第2列}を排除した小行列
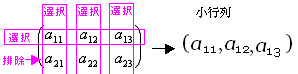
(ex 2-1) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列{第1列, 第2列,第3列}全てを選択した小行列
(ex 2-2) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列から{第1列, 第2列}を選択・第3列を排除した小行列
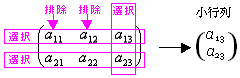
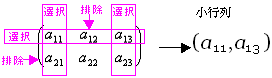
(ex 2-3) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列から{第1列, 第3列}を選択・第2列を排除した小行列
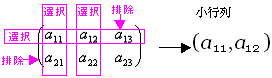
(ex 2-4) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列から{第2列, 第3列}を選択・第1列を排除した小行列
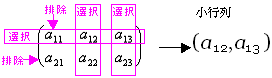
(ex 2-5) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列から{第1列}を選択・{第2列,第3列}を排除した小行列
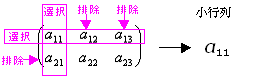
(ex 2-6) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列から{第2列}を選択・{第1列,第3列}を排除した小行列
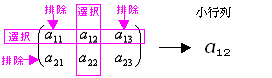
(ex 2-7) Aの2個の行から{第1行}を選択・{第2行}を排除、Aの3個の列から{第3列}を選択・{第1列,第2列}を排除した小行列
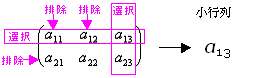
(ex 3-1) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列{第1列, 第2列,第3列}全てを選択した小行列
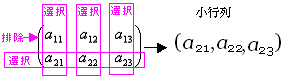
(ex 3-2) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列から{第1列, 第2列}を選択・第3列を排除した小行列
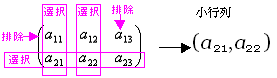
(ex 3-3) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列から{第1列, 第3列}を選択・第2列を排除した小行列
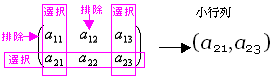
(ex 3-4) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列から{第2列, 第3列}・第1列を排除を選択した小行列
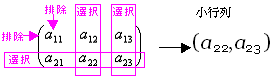
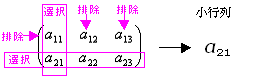
(ex 3-5) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列から{第1列}を選択・{第2列,第3列}を排除した小行列
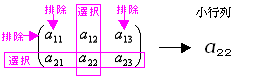
(ex 3-6) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列から{第2列}を選択・{第1列,第3列}を排除した小行列
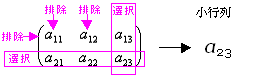
(ex 3-7) Aの2個の行から{第2行}を選択・{第1行}を排除、Aの3個の列から{第3列}を選択・{第1列,第2列}を排除した小行列
|