実ベクトル空間における同型写像：トピック一覧　

・定義：同型写像、同型　　
・定理：同型の反射律･対称律･推移律　
※実ベクトル空間のあいだの一次写像関連ページ：
　　一次写像－定義/ベクトル演算の一次写像/一次写像の代数系/一次写像と線形独立/一次写像―全射･単射　　
　　同型写像/同型写像と線形独立　　

→線形代数目次　
→総目次　
 　

定義：同型写像・同形写像　linear isomorphism　　

　[『岩波数学辞典』210線形空間:B(p.570);砂田『行列と行列式』§5.1C(p.159);斎藤『線形代数入門』４章§2(p.98)
　　永田『理系のための線形代数の基礎』1.3(p.20);ホフマン『線形代数学I』3.3同型(p.86);　
　　佐武『線形代数学』Ⅲ§7(pp.119-120);藤原『線形代数』4.1(pp.93-4);志賀『線形代数30講』16講(p.104);]
【舞台設定】
R：実数体(実数をすべて集めた集合）　　
V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　
V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　
f：V→V'：実ベクトル空間Vから実ベクトル空間V'への写像　
【本題】
同型写像linear isomorphismとは、全単射である一次写像のこと。
つまり、
「写像f が、VからV'への同型写像である」とは、
　写像f が、次の2要件を満たすことをいう。　
　要件1：　写像f が、VからV'への一次写像であること。
　　　論理記号で表すと、すなわち、　
　　　　(1-1)　(∀x,y∈V) ( f ( x+y )=f ( x )+f ( x ) )　　
　　　　(1-2)　(∀x∈V) (∀a∈R) ( f (a x )=af ( x ) )　　
　要件2：　f が全単射であること。[→一次写像が単射・全射となるための必要十分条件]　
　　　論理記号で表すと、すなわち、　
　　　　(2-1) f (V)=V'　　つまり、Imagef=V'　　
　　　　(2-2) 　v,v'∈Vかつf ( v )=f ( v' )　⇒　v =v' 　
※代数系一般における同形写像の定義、線形独立と同型写像、計量同型写像　
→[トピック一覧：同型写像]
→線形代数目次・総目次


→トピック一覧：同型写像
→線形代数目次・総目次

定義：同型・同形　　　

　[『岩波数学辞典』210線形空間:B(p.570);砂田『行列と行列式』§5.1C(p.159);斎藤『線形代数入門』４章§2(p.98)
　　永田『理系のための線形代数の基礎』1.3(p.20);ホフマン『線形代数学I』3.3同型(p.86);　
　　佐武『線形代数学』Ⅲ§7(pp.119-120);藤原『線形代数』4.1(pp.93-4);志賀『線形代数30講』16講(p.104);]
【舞台設定】
R：実数体(実数をすべて集めた集合）　　
V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　
V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　
【本題】
・「VはV'に同型である」とは、VからV'への同型写像が存在することをいう。
・「VはV'に同型である」を次の記号で表す。
　　　　　

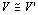
定理：同型の性質　　　

　　[砂田『行列と行列式』§5.1C(p.159);藤原『線形代数』4.1(p.94);斎藤『線形代数入門』４章§2(p.98);　　
　　　ホフマン『線形代数学I』3.3同型(p.86);志賀『線形代数30講』16講(p.104);]　　
【舞台設定】
R：実数体(実数をすべて集めた集合）　　
V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　
V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　
V'' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　
【本題】
(1)反射律　
　　　
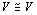
　　　つまり、VからVへの写像は、同型写像
(2)対称律　
　　　⇒
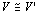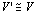
　　　つまり、同型写像の逆写像も同型写像
(3)推移律　
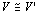　　　かつ⇒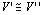
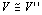
　　　つまり、同型写像の合成写像は同型写像

→トピック一覧：同型写像
→線形代数目次・総目次

定義：正則な写像　regular, nonsingular　

　[志賀『線形代数30講』16講(p.102;104);『岩波数学辞典』210線形空間:B線形写像(p.570);
　　ホフマン『線形代数学I』3.2基底と次元(p.82);　
【舞台設定】
R：実数体(実数をすべて集めた集合）　　
【本題】
・ホフマン『線形代数学I』3.2基底と次元(p.82)は、単射（Ⅰ対１写像）である一次写像（これは、そのKernelが{0}であることと同値）を正則な写像と呼ぶ。
・志賀『線形代数30講』16講(p.102;104)は、一次写像f :V→V'が、単射（Ⅰ対１写像）であり、かつ、dimV=dimV'であるものを正則写像と呼んでいる。

　
　

(reference)

日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、16講線形写像(pp.100-105)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.3基底と次元(pp.41-50)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§7底の変換・直交変換(pp.119-120)。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、4.1線形空間と写像(p.91)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第４章§2線形空間(p.98)。
砂田利一『現代数学への入門：行列と行列式』2003年、§5.1(p.159).

数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。