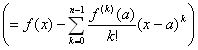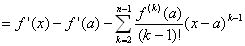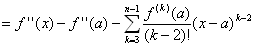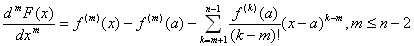テイラーの定理 (本格版)
f (x)を区間Iでn階微分可能な関数とする。 a∈Iを定点、x∈I を任意の点とするとき、
以下の式を満たす点cがxとaの間に存在する (つまり c = a +θ( x−a ), 0<θ<1 )。
f(x)=f(a)+f ' (a) (x−a) /(1! )+ f '' (a) (x−a)2/(2! )+…+f (n-1) (a) (x−a)n-1/(n-1)!+Rn 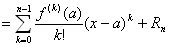
Rn= f (n) (c) (x−a)n /(n! )
証明 : テイラーの定理 (本格版)
[参照:高木『解析概論』61. 小平『解析入門I』132. 高橋『経済学とファイナンスのための数学』62.]
仮定: ・f(x)は区間Iでn回微分可能な関数 …(1)
・a, x∈I …(2)
F(x) = Rn= f(x)−f(a)−f ' (a) (x−a) /(1! ) −f '' (a) (x−a)2/(2! ) −f ''' (a) (x−a)3/(3! )…−f (n-1) (a) (x−a)n-1/(n-1)!
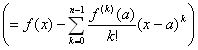
と置く。
すると、
F(a)=F' (a) = F''(a)=…=F(n-1)(a)=0 …(3)
F(n)(x)= f (n) (x) …(4)
なぜなら、 F (x)を順次微分してゆくと、
dF (x)/dx = f ' (x)−{ f ' (a) /(1! )}{(x−a)}’−{ f '' (a)/(2! )}{(x−a) 2}’−{ f ''' (a)/(3! )}{(x−a)3}’…
…−{ f (n-1) (a)/(n-1)!}{(x−a)n-1}’
∵定数の微分、関数の和の微分、関数の定数倍の微分、
f(a)=f ' (a) =f '' (a) =…=f (n-1) (a) は定数なので注意。
= f ' (x)−{ f ' (a) /(1! )}−{ f '' (a)/(2! )}{2(x−a)}−{ f ''' (a)/(3! )}{3(x−a)2}…
…−{ f (n-1) (a)/(n-1)!}{ (n-1) (x−a)n-2}
∵合成関数の微分
= f ' (x)−f ' (a)−{ f '' (a)/(1! )}(x−a)−{ f ''' (a)/(2! )}(x−a)2…−{ f (n-1) (a)/(n-2)!}(x−a)n-2
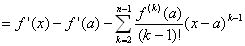
d2F(x) /dx2 = f '' (x)−{ f '' (a)/(1!)}{(x−a)}’−{ f ''' (a)/(2! )}{(x−a)2}’…−{ f (n-1) (a)/(n-2)!}{ (x−a)n-2}’
∵定数の微分、関数の和の微分、関数の定数倍の微分、
f(a)=f ' (a) =f '' (a) =…=f (n-1) (a) は定数なので注意。
= f '' (x)−f '' (a)/(1!)−2f ''' (a)(x−a)/(2! )−3f '''' (a)(x−a)2/(3! )…−(n-2)f (n-1) (a)(x−a)n-3/(n-2)!
∵合成関数の微分
= f '' (x)−f '' (a)−f ''' (a)(x−a)/(1! )−f '''' (a)(x−a)2/(2! )…−f (n-1) (a)(x−a)n-3/(n-3)!
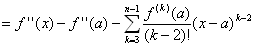
・
・
・
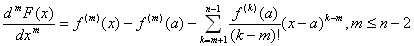
・
・
・
dn-2F(x)/dxn-2=f (n-2) (x)−f (n-2) (a)−f (n-1) (a)(x−a)
dn-1F(x)/dxn-1=f (n-1) (x)−f (n-1) (a)
dnF(x)/dxn=f (n) (x)
※関数の和の高階導関数、ベキ関数の高階導関数などの公式を使うと、
もっとスッキリ展開できるはず。
G(x)=(x−a) n と置く。G(a)=0 …(5) x≠aで、G(x)≠0. …(6)
G(a)=G'(a)=G''(a)=…=G ( n-1 ) (a)=0 …(7)
なぜなら、
G'(x)= n(x−a) n−1 ∵合成関数の微分
G''(x)= n (n−1)(x−a) n−2 ∵合成関数の微分
G(3)(x)= n (n−1) (n−2) (x−a) n−3 ∵合成関数の微分
・
・
・
G(n-1)(x)= n (n−1) (n−2) …(n−(n-1-1)) (x−a) n−(n-1)= n (n−1) (n−2) …2 (x−a)
G(n)(x)= n (n−1) (n−2) … (n−(n-1)) (x−a) n−n= n (n−1) (n−2) …・1・1=n! …(7')
(i) a<xの場合
(step1)
F(x)/G(x) = (F(x)−F(a)) / (G(x)−G(a)) ∵(3)よりF(a)=0、(5)よりG(a)=0
(1) (2)より閉区間[a,x]で連続微分可能。(6)より開区間(a,x)でG(x)≠0。
したがって、コーシーの平均値定理を適用して、
F(x)/G(x) = (F(x)−F(a)) / (G(x)−G(a)) = F' ( c1 ) / G' ( c1 )
を満たすc1が、開区間 (a,x)に存在する。
(step2)
同様に、(3) (7)よりF' (a)=0、G' (a) =0、コーシーの平均値定理より、
F' ( c1 ) / G' ( c1 ) = ( F' (c1)−F' (a) ) / (G' (c1)−G' (a)) = F''( c2 ) / G''( c2 )
を満たすc2が、開区間 (a, c1)に存在する。
・
・
・
(stepN)
同様に、(3) (7)よりF(n-1)(a) =0、G(n-1)(a) =0、コーシーの平均値定理より、
F(n-1)(cn-1)/G(n-1)(cn-1)= (F(n-1)(cn-1)−F(n-1)(a))/(G(n-1)(cn-1)−G(n-1)(a))=F(n)(cn)/G(n)(cn)
= f (n) ( cn )/n! (∵(4), (7'))
を満たすcnが、開区間 (a, cn−1 )に存在する。
つまり、
F(x)/G(x) =F' ( c1 ) / G' ( c1 ) = F''( c2 ) / G''( c2 )=…=F(n-1)(cn-1)/G(n-1)(cn-1)=F(n)(cn)/G(n)(cn)= f (n) ( cn )/n!
を満たすci (1≦i≦n、i∈N)が
a<cn <cn−1 <…<c2< c1<x
に存在する。
これを簡単にして、G(x)を(x−a) n に戻すと、
F(x)/(x−a) n=f (n) ( cn )/n! すなわち、F(x) =f (n) ( cn )(x−a) n/n!
を満たすcnが開区間(a,x)に存在する。
との結論に至る。
(ii) x< aの場合
(step1)
F(x)/G(x) = (F(x)−F(a)) / (G(x)−G(a)) ∵(3)よりF(a)=0、(5)よりG(a)=0
(1) (2)より閉区間[a,x]で連続微分可能。(6)より開区間(a,x)でG(x)≠0。
したがって、コーシーの平均値定理を適用して、
F(x)/G(x)=(F(x)−F(a))/(G(x)−G(a))=−(F(a)−F(x))/−(G(a)−G(x))= (F(a)−F(x))/(G(a)−G(x))
= F' ( c1 ) / G' ( c1 )
を満たすc1が、開区間(x, a)に存在する。
(step2)
同様に、 (3) (7)より F'(a)=0、G'(a)=0、コーシーの平均値定理より、
F' ( c1 ) / G' ( c1 ) = ( F' (a)−F' (c1)) / (G' (a)−G' (c1)) = F''( c2 ) / G''( c2 )
を満たすc2が、開区間 (c1, a)に存在する。
・
・
・
(stepN)
同様に、(3) (7)よりF(n-1)(a) =0、G(n-1)(a) =0、コーシーの平均値定理より、
F(n-1)(cn-1)/G(n-1)(cn-1)= (F(n-1)(a)−F(n-1)(cn-1))/(G(n-1)(a)−G(n-1)(cn-1))=F(n)(cn)/G(n)(cn)
= f (n) ( cn )/n! (∵(4), (7'))
を満たすcnが、開区間 (cn−1 , a)に存在する。
つまり、
F(x)/G(x) =F' ( c1 ) / G' ( c1 ) = F''( c2 ) / G''( c2 )=…=F(n-1)(cn-1)/G(n-1)(cn-1)=F(n)(cn)/G(n)(cn)= f (n) ( cn )/n!
を満たすci (1≦i≦n、i∈N)が
x < c1 < c2<…< cn−1 < cn < a
に存在する。
これを簡単にして、G(x)を(x−a) n に戻すと、
F(x)/(x−a) n=f (n) ( cn )/n! すなわち、F(x) = f (n) ( cn )(x−a) n/n!
を満たすcnが開区間(x,a)に存在する。
との結論に至る。