→戻る 　

定理：指数関数の微分公式

・( a x ) ' = a x  log a　 ( ただし a >0 )　
・( e x ) ' = e x　　

【文献】

　・高木『解析概論』pp.45-46
　・吹田・新保『理工系の微分積分学』p.38
　・矢野・田代『社会科学者のための基礎数学』p.84
　・高橋『経済学とファイナンスのための数学』p.51
　・『微分積分』p.61;


→戻る　

証明1　：　微分係数の定義までもどる証明　　　

　【文献】
　　　・吹田・新保『理工系の微分積分学』p.38
　　　・高橋『経済学とファイナンスのための数学』p.51
　　　・高木『解析概論』pp.45-46.

　　 f (x) = a x 　とおく。
　　x =x0における微分係数 f ' (x0)：
　　　f ' (x0)　　　　∵微分係数の定義　
　　　　　　　　　　　　　　　
　　ここで、t = a h −１　とおく。　h→０で、 t→０　。　
　　また、a h = t ＋１　となって、すなわち、
　　　h = log a ( t ＋１)　　　　　　∵対数の定義　
　　　　＝ loge( t ＋１)／log e a 　　∵底の変換公式　　
　　　　　　　（a >0、t>−１より、(t＋１)＞０なので、対数をとるにあたって問題なし）
　　したがって、x =x0における微分係数 f ' (x0) は、t を用いて以下のように書ける。
　　　f ' (x0)　　　　　 　　…※　　　
　　 ところで、
　　　　　∵対数の性質　
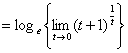　　　　　　　　　　　　　　　　　　　∵定理　、定理　　

　　　　　　　　　　＝log e e　＝１
　t→0で、log(t+1)とtの比が1なので、分子と分母を入れ替えても同じこと。
　よって、
　この結果を※に代入して、
　　　　　f ' (x0) 　= ax0 log a　　
　なお、a=eのとき、すなわち、f(x0) = ex0 　　では、　f ' (x0)＝ex0 log e ＝ex0　




　→戻る　　

(証明2：対数微分法を用いた証明)

　　[『微分積分』p.61, 矢野田代『社会科学者のための基礎数学』p.84]

　　　　手順1. 両辺の絶対値の対数をとる。　　
　　　　　　　　　　　　log| f (x)|　＝　log | ax |　
　　　　　　　　　　　　log f (x) 　＝　log ax　　　　∵指数関数の値域は正の実数全体。
　　　　　　　　　　　　log f (x) 　＝　x log a　　　　∵対数の性質　　　
　　　　手順2. 両辺をそれぞれxで微分する。左辺には関数の対数の微分を適用。
　　　　　　　　　(　log f (x)　)’＝　(　x log a　)’
　　　　　　　　　　　　f ' (x)／f(x)＝　log a　
　　　　手順3. 整理　　f ' (x)＝ f(x)・log a　　＝ a x・log a　　

　→戻る