(
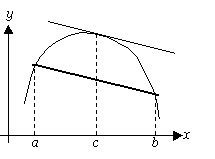
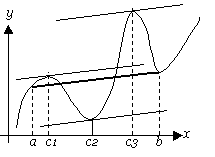
解釈) 閉区間[a,b]で連続、開区間(a,b)で微分可能な関数y=f(x)を考えると、区間の両端を結んだ直線と平行な接線ををひける点が、
(a,b)内に少なくとも一つ存在する。
→
戻る 平均値定理 mean value theorem, law of the mean関数
y=f(x)は閉区間[a,b]で連続、開区間(a,b)で微分可能ならば、(区間の端点では微分可能でなくてもよい)|
( 解釈) 閉区間[a,b]で連続、開区間(a,b)で微分可能な関数y=f(x)を考えると、区間の両端を結んだ直線と平行な接線ををひける点が、 (a,b)内に少なくとも一つ存在する。 |
|
|
|
|
→
戻る(
平均値定理の証明)[
矢野田代『社会科学者のための…』p.77;吹田新保『理工系の…』pp.44-45;和達『微分積分』pp.59-60.](仮定)
y=f(x)は閉区間[a,b]で連続、開区間(a,b)で微分可能…(1)
![]()
h(x)= f(x)−g(x)
とおく。
y=g(x)は、y=f(x)の区間の両端を結んだ直線、
h(x)は、y=f(x)とこのような直線との差を表すと解釈できる。
(本題)
[h(x)はロールの定理を適用する条件が整っている。]
g(x)が一次関数なので連続かつ微分可能であることと(1)より、
h(x)も閉区間[a,b]で連続、開区間(a,b)で微分可能。…(2)
∵
関数の和差積商の連続性、関数の和差の微分h(a)= f(a)−g(a)= f(a)−f(a) =0
h(b)= f(b)−g(b)= f(b)−g(b) =0
( そもそも、
x=a,bでy=f(x)と交わるように直線y=g(x)を決めたのだから、x=a,bでy=f(x)とy=g(x)の差がゼロになるのはあたりまえ。)
よって、
h(a)= h(b) …(3)(2)、(3)より、h(x)についてロールの定理が成り立つ。
[h(x)にロールの定理を適用]
ゆえに、
ロールの定理より、h' (c)=0
を満たす
cが開区間(a,b)内に少なくとも一つ存在する。 …(4)[h(x)の導関数を求める]
ところで
h(x)の導関数は、h'(x)= f ' (x)−g' (x)
![]() …
…
[結論]
(5)を用いて(4)を言い直すと、
![]()
すなわち、
![]()
を満たす
cが開区間(a,b)内に少なくとも一つ存在する、となる。|
→ 戻る |