リーマン・スチルチェス積分 Riemann-Stieltjes integral
前:有界変動、スチルチェス積分の定義
続:スチルチェス可積分条件、スチルチェス積分の性質(2)
→総目次
III. リーマン・スチルチェス積分の性質(その1)
定理:スチルチェス積分の線形性(1)
[杉浦『解析入門I』352.; ルディン『現代解析学』項目6-10;高橋『経済学とファイナンスのための数学』96.]
関数f(x), g(x)が閉区間I [a,b]上で単調増加関数t(x)に関しスチルチェス積分可能ならば、
f(x)+g(x)、c f(x) (c:定数)も、閉区間I [a,b]上で単調増加関数t(x)に関しスチルチェス積分可能となり、
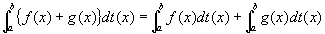
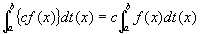
証明:
杉浦『解析入門I』353. は、リーマン積分の線形性とまったく同じとしている。
定理:スチルチェス積分の線形性(2)
[杉浦『解析入門I』352.; Lang, Real and Functional Analysis282; ルディン『現代解析学』項目6-10;高橋『経済学とファイナンスのための数学』96.]
関数f(x)が閉区間I [a,b]上で関数t(x), s(x)に関しスチルチェス積分可能ならば、
関数f(x)は、閉区間I [a,b]上で関数t(x)+s(x),t(x)-s(x) ,ct(x)(c:定数)に関しスチルチェス積分可能となり、
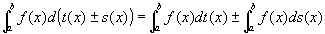
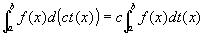
証明:[杉浦『解析入門I』353. ]
関数f(x)の関数t(x)+s(x)に関する(分割⊿・代表点{ζk}とした際の)スチルチェス和は、

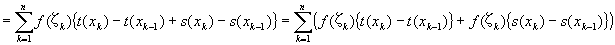
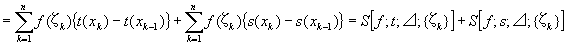
というふうに、
(分割⊿・代表点{ζk}とした際の) f(x)のt(x)に関するスチルチェス和と、
(分割⊿・代表点{ζk}とした際の) f(x)のs(x)に関するスチルチェス和との、和になっている。
つまり、 S [ f ; t+s ;⊿;{ζk}]=S [ f ; t ;⊿;{ζk}]+ S [ f ; s ;⊿;{ζk}] …①
f(x)が閉区間 [a,b]上でt(x), s(x)に関しスチルチェス積分可能ならば、
分割の幅|⊿|→0で、①の右辺は、
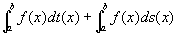
に収束するので、①の左辺も、これに収束する。
よって、f(x)が閉区間 [a,b]上で関数t(x), s(x)に関しスチルチェス積分可能ならば、
関数f(x)は、閉区間I [a,b]上で関数t(x)+s(x) に関しスチルチェス積分可能となり、
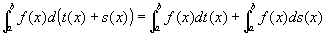
定理:スチルチェス積分の部分積分公式
[杉浦『解析入門I』353. Lang, Real and Functional Analysis282 ;高橋『経済学とファイナンスのための数学』97.]
関数f(x)が閉区間[a,b]上で関数t(x) に関しスチルチェス積分可能ならば、
関数t(x)は閉区間[a,b]上で関数f(x) に関しスチルチェス積分可能となり、
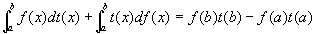
証明:
杉浦『解析入門』353、Lang, Real and Functional Analysis282 -3を見よ。
定理:スチルチェス積分の単調性
[杉浦『解析入門I』357.; ルディン『現代解析学』項目6-10;高橋『経済学とファイナンスのための数学』96.]
cf. リーマン積分の単調性
関数t(x)が閉区間[a,b]上で単調増加、
かつ、
関数f(x), g(x)が閉区間[a,b]上で関数t(x)に関しスチルチェス積分可能、
かつ、
閉区間[a,b]上でつねに、f(x)≦g(x)となるならば、
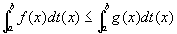
証明:
杉浦『解析入門I』353 は、リーマン積分の単調性とまったく同じとしている。
定理:スチルチェス積分の三角不等式
[杉浦『解析入門I』357;]
cf. リーマン積分の三角不等式
関数t(x)が閉区間[a,b]上で単調増加、
かつ、
関数f(x)が閉区間[a,b]上で関数t(x)に関しスチルチェス積分可能であるならば、
| f(x)|も関数t(x)に関しスチルチェス積分可能となって
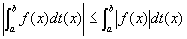
証明:
杉浦『解析入門I』353 は、リーマン積分の三角不等式とまったく同じとしている。
定理:スチルチェス積分の第1平均値定理
[杉浦『解析入門I』357;]
cf.リーマン積分の第1平均値定理、
関数t(x)が閉区間[a,b]上で単調増加 (仮定1)、
かつ、
関数f(x)が閉区間[a,b]上で関数t(x)に関しスチルチェス積分可能であり(仮定2)、
かつ、
閉区間[a,b]における関数f(x)の上限がM、下限がmである(仮定3)
ならば、
(結論1)
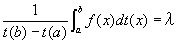
m≦λ≦M
を満たすλが存在する。
(結論2) 仮定1~3に加えて、関数f(x)が閉区間[a,b]上連続であるならば(仮定4)、
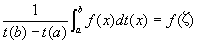
a≦ζ≦b
を満たすζが存在する。
証明:
杉浦『解析入門I』358.はリーマン積分の第1平均値定理とまったく同じとしている。
( reference )
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.93-99;104-106.
高木貞治『解析概論:改訂第3版』岩波書店、1983年、pp. 129-132;443-445.
杉浦光夫『解析入門I』東京大学出版会、1980年、p.345;pp.349-361.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ-ルタ-・ルディン『現代解析学』共立出版、1971年、第6章。
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.224-5:Exercisesとして。
Lang,Serge.Real and Functional Analysis(Graduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1993,pp.278-287.
Ross,Kenneth A.Elementary Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1980,pp.203-221.