リーマン・スチルチェス積分 Riemann-Stieltjes integral
続:スチルチェス積分の定義・性質(1)、スチルチェス可積分条件、スチルチェス積分の性質(2)
→総目次
有界変動の定義
定義:変動量 variation
[高木『解析概論』pp. 129-131; 杉浦『解析入門』345; Lang, Real and Functional Analysis278-9;
高橋『経済学とファイナンスのための数学』104-105.]
閉区間[a,b]における分割⊿に対する関数f(x)の変動量とは、分割⊿でつくった各小区間の左端と右端とでf(x)の値にどれだけひらきがあるのかを、全ての小区間について足し合わせたもの。
つまり、
閉区間[a,b]をI1=[a, x1], I2=[x1 , x2],…,In=[xn‐1 , b] (a=x0<x1<x2<…<xn=b)に分ける分割⊿
に対する関数f(x)の変動量v⊿は、
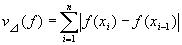
で定義される。
絶対値の和であるから、v⊿≧0であることに注意。
定義:有界変動bounded variation、総変動量
[高木『解析概論』p.129; 杉浦『解析入門』345; Lang, Real and Functional Analysis278-9; 高橋『経済学とファイナンスのための数学』104-105.]
→利用例:スチルチェス積分可能であることの十分条件
閉区間[a,b]における分割⊿に対する関数f(x)の変動量v⊿は、分割⊿のとり方をいじることで、小さくなったり、大きくなったりする。
変動量v⊿がとりうる値の範囲 ―分割⊿の全てのとり方に対応した変動量v⊿の範囲― が有界であるならば、
関数f(x)は閉区間[a,b]において有界変動であるといい、
変動量v⊿がとりうる値の範囲の上限(最小上界)supを、総変動量とよぶ。
(→実数の集合が、上に有界ならば、supをもつ)
すなわち、閉区間[a,b]における関数f(x)の総変動量V(f)は、
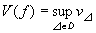
で、定義される。
定理:総変動量の区間加法性
[高木『解析概論』p.130;杉浦『解析入門』350.]
(1)
関数f(x)が閉区間[a,b]において有界変動ならば、
任意のc∈[a,b]に対し、f(x)は閉区間[ a , c ]、[ c , b ]において有界変動であり、逆も成り立つ。
(2)
関数f(x)が閉区間[a,b]において有界変動ならば、
任意のc∈[a,b]に対し、
[a,b]におけるf(x)の総変動量=[a,c]におけるf(x)の総変動量+[c,b]におけるf(x)の総変動量
(1)の証明:
[f(x)が閉区間[a,b]において有界変動⇒f(x)は閉区間[ a , c ]、[ c , b ] (∀c∈[a,b]) において有界変動]
設定:
・[a,c]についての任意の分割を⊿a、[c,b] についての任意の分割を⊿bで表すことにする。
・[a,c]については⊿aで分割し[c,b]については⊿bで分割する[a,c]の分割を⊿1で表すことにする。
仮定:f(x)が閉区間[a,b]において有界変動で、閉区間[a,b]における関数f(x)の変動量v⊿には、上限(最小上界)V(f;a,b)が存在する。
本論:
変動量v⊿の定義から、 v⊿a(f;a,c)+ v⊿b(f;c,b)= v⊿1(f;a,b) …(1)
(1)式左辺の⊿a、⊿bについての上限をとると、←?ここですでに、結論の有界変動が、仮定されていないか?
Sup v⊿a(f;a,c)+ Sup v⊿b(f;c,b)=sup(v⊿a(f;a,c)+ v⊿b(f;c,b))
∵上限の和の定理より、v⊿a(f;a,c)、v⊿b(f;c,b)が上に有界であるならば。
右辺に(1)式右辺を代入して、
Sup v⊿a(f;a,c)+ Sup v⊿b(f;c,b)=sup v⊿1(f;a,b)
また、仮定より、v⊿1(f;a,b)≦V(f;a,b)
V (f;a,c)+V(f;c,b) ≦V(f;a,b)
[f(x)は閉区間[ a , c ]、[ c , b ] (∀c∈[a,b]) において有界変動⇒f(x)が閉区間[a,b]において有界変動]
定義:正の変動 positive variation
定義:負の変動 negative variation
定義: 全変動 total variation
[高木『解析概論』p.129; 高橋『経済学とファイナンスのための数学』104-105.]
(1) p⊿ 、-n⊿ 、 n⊿
閉区間[a,b]をn個の小区間I1=[a, x1], I2=[x1 , x2],…,In=[xn‐1 , b] (a=x0<x1<x2<…<xn=b)に分ける分割⊿を考えよう。
各小区間の左端の右端のf(x)の差:f(xi)-f(xi-1)は、小区間によって、プラスだったりマイナスだったりする。
ここで、f(xi)-f(xi-1)がプラスになる小区間とマイナスになる小区間とをよりわけて、足し合せたものを考えてみよう。
つまり、
プラスになる小区間でのf(xi)-f(xi-1)のみを、すべてのプラスになる小区間について足し合せた和を、p⊿
マイナスになる小区間でのf(xi)-f(xi-1)のみを足し合せた和(これはマイナスの値となる)を、すべてのマイナスになる小区間について足し合せた和を、-n⊿
マイナスになる小区間でのf(xi)-f(xi-1)を、すべてのマイナスになる小区間について足し合せた和の符号を反転させてプラスの値にしたものを、n⊿
で表すことにする。
すると、
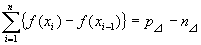
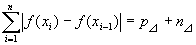
よって、
閉区間[a,b]における分割⊿に対する関数f(x)の変動量v⊿=p⊿+n⊿
また、
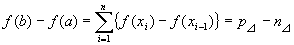
(2) P、N、-N
閉区間[a,b]における分割⊿に対する関数f(x)の変動量v⊿ 、p⊿、n⊿、-n⊿は、分割⊿のとり方をいじることで、小さくなったり、大きくなったりする。
f(x)が有界変動ならば、f(x)の変動量v⊿=p⊿+n⊿は有界で、上限(最小上界)Vをもつ。
ゆえに、f(x)が有界変動ならば、v⊿ のみならず、p⊿、n⊿、-n⊿も有界となり、上限(最小上界)Vをもつ。
これらの上限を、P、N、-Nで表す。
すると、f(x)の変動量v⊿が上限(最小上界)Vとなるような分割⊿をおこなった場合、
二つの等式v⊿=p⊿+n⊿、f(b)-f(a)= p⊿-n⊿は、
V=P+N、
f(b)-f(a)=P-N
と書ける。
(3)正の変動P(x)、負の変動N(x)、全変動V(x)
閉区間[a,b]内の一点をxとおく。すると、総変動量の区間加法性より、関数f(x)が閉区間[a,b]において有界変動となるならば、閉区間[a,x]においてもf(x)も有界変動となり、閉区間[a,x]におけるf(x)の変動量v⊿の上限(最小上界):V、p⊿、n⊿、-n⊿の上限(最小上界):P、N、-Nが存在する。
このとき、xを閉区間[a,b]内で動かせば、V,P,Nはxの関数となるので、
V(x)、P(x),N(x)と書く。
V(x)を、閉区間[a,b]におけるf(x)の全変動
P(x) を、閉区間[a,b]におけるf(x)の正の変動、
N(x) を、閉区間[a,b]におけるf(x)の負の変動
と呼ぶ。
また、(2)より、
V(x)=P(x)+N(x)、
f(x)-f(a)=P(x)-N(x)
が成り立つ。
有界変動関数の性質
[高木『解析概論』p.131; 杉浦『解析入門』349-351;高橋『経済学とファイナンスのための数学』105.]
定理:有界変動関数は有界
[高木『解析概論』p.129;杉浦『解析入門I』349.]
関数f(x)が閉区間[a,b]において有界変動ならば、関数fは閉区間[a,b]において有界 [杉浦『解析入門I 』349.]
[証明 『解析入門I 』349.]
設定:閉区間[a,b]を点x∈[a,b]で二つに分ける分割を、⊿1で表すことにする。…(1)
仮定:関数f(x)が閉区間[a,b]において有界変動であるとする。
これは、すなわち、
閉区間[a,b]における分割⊿に対する関数f(x)の変動量v⊿(f)は、
分割⊿のとり方を変えると様々な値をとりうるが、 、
変動量v⊿(f)がとる値の範囲の上限(最小上界)=総変動量V(f)は有界である、…(2)
という意味である。
本論:
総変動量の定義より、任意の分割⊿に対して、変動量v⊿( f )≦総変動量V( f )
よって、(1)の分割⊿1に対する関数f(x)の変動量v⊿ 1 ( f )≦総変動量V( f ) …(3)
変動量の定義から、v⊿ 1 ( f )=|f(x)-f(a)|+|f(b)-f(x)|
よって、|f(x)-f(a)|≦v⊿ 1 ( f ) …(4)
(3)(4)を合せて、|f(x)-f(a)|≦v⊿ 1 ( f ) ≦V( f )
つまり、|f(x)-f(a)|≦V( f )
だから、|f(x)|≦|f(a)| +V( f ) ←なんで?!
(2)より、V( f ) は有界だから、fは閉区間[a,b]において有界となる。 ←でも、|f(a)|が有界でなかったら?
|f(x)-f(a)|≦|f(x)|+|-f(a)|
定理:有界変動関数の和差積も有界変動
[高木『解析概論』p.130;杉浦『解析入門I』350.]
関数f(x) , g(x)が閉区間[a,b]において有界変動ならば、
和f(x)+g(x) 、差f(x)-g(x) 、積f(x) g(x) も閉区間[a,b]において有界変動である。
定理:単調関数は有界変動
[杉浦『解析入門I』345.]
閉区間[a,b]上の実数値の単調関数f(x)は有界変動。
(証明)
閉区間[a,b]の任意の分割⊿に対応する変動量v⊿(f)は
v⊿(f)=|f(b)-f(a)|
になるから。
定理:有界変動関数は二つの単調増加関数の差に等しい。
[高木『解析概論』p.130;杉浦『解析入門I 』351;高橋『経済学とファイナンスのための数学』105.]
以下の命題Aと命題Bは同値。
A: 関数f(x)が閉区間[a,b]において有界変動である
B: 閉区間[a,b]において、関数f(x)は二つの単調増加関数の差として表される。
証明:B⇒A
定理「単調関数は有界変動」と、定理「有界変動関数の和差積は有界変動」から。
証明: A⇒ B
定理:ある関数が有界変動となるための十分条件
[高木『解析概論』p.131; 杉浦『解析入門I』345;高橋『経済学とファイナンスのための数学』105-106.]
1.
絶対連続ならば、有界変動[高橋]
微分可能ならば、絶対連続であって、有界変動
2.
リプシッツ連続(→杉浦p.226File123)ならば、[杉浦]
微分可能で導関数が有界ならば、リプシッツ連続で有界変動[杉浦]
連続微分可能(C1級)ならば、リプシッツ連続で有界変動[杉浦]
※積分関数は有界変動[高木『解析概論』p.131;.]。
(reference)
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.93-99;104-106.
高木貞治『解析概論改訂第3版』岩波書店、1983年、pp. 129-132.
杉浦光夫『解析入門I』東京大学出版会、1980年、p.345;pp.349-361.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ-ルタ-・ルディン『現代解析学』共立出版、1971年、第6章[6.21-6.27]。
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.224-5:Exercisesとして。
Lang,Serge.Real and Functional Analysis(Graduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1993,pp.278-287.
Ross,Kenneth A.Elementary Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1980,pp.203-221.