◎反射率：
　散乱光の強さを考える場合，光線密度だけでなく，光線の雨滴内での屈折・反射に伴う光エネルギーの減衰も考慮する必要があります。以下では，この点について吟味してみましょう。
　光は横波であり，互いに独立な２つの直線偏光成分に分解できます。

　上図のように，屈折率 $n_1$ の媒質 $\mathrm{I}$ と屈折率 $n_2$ の媒質 $\mathrm{II}$ との境界面に，光波が入射角 $\theta_1$ で入射し，屈折角 $\theta_2$ で屈折している場合を考える。このとき光波の２偏光成分を，入射光と反射光とを含む面（入射面。上図の面）内の成分（平行成分） $\phi_\para$ と，入射面に垂直な方向の成分（垂直成分） $\phi_\prep$ とすると，電磁波の理論により，それぞれの成分の反射波の振幅反射率 $r_\para$ ， $r_\prep$ はそれぞれ，\[r_\para = \bun{n_2 \cos\theta_1 - n_1\cos\theta_2}{n_2 \cos\theta_1 + n_1 \cos\theta_2} \quad \cdots\cdots\maru{6} \\ r_\prep = \bun{n_1 \cos\theta_1 - n_2\cos\theta_2}{n_1 \cos\theta_1 + n_2 \cos\theta_2} \quad \cdots\cdots\maru{7} \]で与えられます（フレネルの式)。

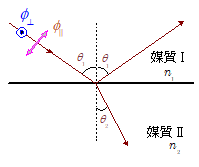
（参考）　 $\maru{6}$式，$\maru{7}$ 式は，入射角 $\theta_1$ ，屈折角 $\theta_2$ のみを使って，以下の $\maru{6}'$ ， $\maru{7}'$ のように表すこともできます。
　まず，屈折の法則より，\[n_1 \sin\theta_1 = n_2 \sin\theta_2 \\ \kern-1em \therefore \bun{n_1}{n_2} = \bun{\sin\theta_2}{\sin\theta_1} \\[1.5em] \kern -2em \therefore r_\para = \bun{n_2 \cos\theta_1 - n_1\cos\theta_2}{n_2 \cos\theta_1 + n_1 \cos\theta_2} \\[1.5em] = \bun{\,\, \cos\theta_1 - \bun{n_1}{n_2}\cos\theta_2 \,\,}{ \cos\theta_1 + \bun{n_1}{n_2} \cos\theta_2} \\[1.5em] = \bun{\,\, \sin\theta_1 \, \cos\theta_1 - \sin\theta_2 \, \cos\theta_2 \,\,}{ \sin\theta_1 \, \cos\theta_1 + \sin\theta_2 \, \cos\theta_2} \\[1.5em] = \bun{ \,\, \uchikesi{\bun{1}{2}} \sin(2\theta_1) - \uchikesi{\bun{1}{2}}\sin(2\theta_2) \,\,}{\uchikesi{\bun{1}{2}}\sin(2\theta_1) + \uchikesi{\bun{1}{2}}\sin(2\theta_2)} \\[1.5em] = \bun{\,\,\uchikesi{2}\, \cos(\theta_1 + \theta_2) \times \sin(\theta_1 - \theta_2)\,\,}{\uchikesi{2}\, \sin(\theta_1 + \theta_2) \times \cos(\theta_1 - \theta_2)} \\[1.5em] = \bun{\tan(\theta_1 - \theta_2)}{\tan(\theta_1 + \theta_2) } \quad \cdots\cdots\maru{6}{}' \\ \kern-1em r_\prep = \bun{n_1 \cos\theta_1 - n_2\cos\theta_2}{n_1 \cos\theta_1 + n_2 \cos\theta_2} \\[1.5em] = \bun{\,\, \bun{n_1}{n_2}\cos\theta_1 - \cos\theta_2 \,\,}{\bun{n_1}{n_2}\cos\theta_1 + \cos\theta_2} \\[1.5em] = \bun{\,\, \sin\theta_2 \, \cos\theta_1 - \cos\theta_2 \, \sin\theta_1 \,\,}{\sin\theta_2 \, \cos\theta_1 + \cos\theta_2 \, \sin\theta_1} \\[1.5em] = - \bun{\sin(\theta_1 - \theta_2)}{\sin(\theta_1 + \theta_2) } \quad \cdot\cdots\maru{7}{}'\]

　光の強さ（＝エネルギー）は振幅の２乗に比例するので，入射光に対する反射光のエネルギーの比（エネルギー反射率） $R$ は，それぞれの偏光成分について，\[ \kern -1em R_\para = r_\para{}^2 = \color{red}{\bigg(\bun{n_2 \cos\theta_1 - n_1\cos\theta_2}{n_2 \cos\theta_1 + n_1 \cos\theta_2} \bigg)^2 } \quad \cdots\cdots\maru{8} \\ \kern -1em R_\prep = r_\prep{}^2 = \color{red}{\bigg(\bun{n_1 \cos\theta_1 - n_2\cos\theta_2}{n_1 \cos\theta_1 + n_2 \cos\theta_2} \bigg)^2} \quad \cdots\cdots\maru{9} \]　また，エネルギー保存より，入射光のエネルギー＝反射光のエネルギー＋透過光のエネルギー　であるから，光のエネルギー透過率は $T$ は，それぞれの偏光成分について，\[ \kern -1em T_\para = 1 - R_\para \\ = \color{red}{\bun{4 n_1n_2\, \cos\theta_1 \, \cos\theta_2}{(n_2 \cos\theta_1 + n_1 \cos\theta_2)^2 } } \quad \cdots\cdots\Maru{10} \\ \kern -1em T_\prep = 1 - R_\prep \\ = \color{red}{ \bun{4 n_1n_2\, \cos\theta_1 \, \cos\theta_2}{(n_1 \cos\theta_1 + n_2 \cos\theta_2)^2 } } \quad \cdots\cdots\Maru{11}\]で与えられる。 $\maru{8} \sim \Maru{11}$ 式に屈折の法則より得られる\[n_1 \sin\theta_1 = n_2 \sin\theta_2 \quad \therefore \theta_2 = \arcsin\bigg(\bun{n_1}{n_2}\sin\theta_1 \bigg) \]を代入すれば， $R_\para$ ， $R_\prep$ ， $T_\para$ ， $T_\prep$ を入射角 $\theta_１$ の関数として求めることができる。
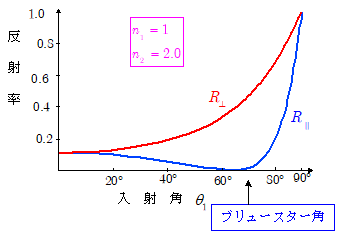
　下図は，屈折率 $n_1=1.0$ ， $n_2=2.0$ の場合のエネルギー反射率のグラフである。
　このとき，反射光の平行成分 $\phi_\para$ の反射率が $0$ になる入射角がある。これは $\maru{6}'$ 式で分母が $\tan(\theta_1 + \theta_2) = \infty$ となる場合で， $\color{blue}{\theta_1 + \theta_2 = \pi/2 }$ 　となるときである。これをブリュースターの法則という。

　次は，　　解説５（虹散乱での反射率と偏光）　をクリック

---

　　虹の話 　　概要
　　解説１（解説１：雨滴による虹散乱）
　　解説２（虹の色と散乱角）
　　解説３（散乱角の詳細計算）
　　解説４（反射率）
　　解説５（虹散乱での反射率と偏光）
　　　＊＊＊　以下，過剰虹　関連　＊＊＊　
　　解説６（波動光学）
　　解説７（過剰虹成因の概要）
　　解説８（波面の式）
　　解説９（虹の光強度の式）
　　解説１０（波動光学による虹）