◎強い散乱光が射出される方向：

　雨滴に太陽光線が当たると，その衝突係数 $y$ （＝光線の入射位置 $b$ ÷雨滴半径 $a$ ）の値によって前ページで求めた $\maru{4}$ 式， $\maru{5}$ 式で与えられる角度の方向に散乱されます。 $0 \le b \le a$ ゆえ $0 \le y \le 1$ であり，観測者の目には雨滴の一滴々々から様々な値の衝突係数 $y$ に基づく様々な色の散乱光が様々な角度で届くことになります。

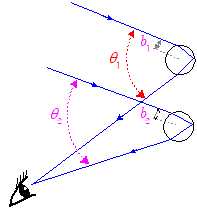
　ではなぜ，虹では特定の方向に特定の色が付いて見えるのでしょうか？

　ある方向からくる光の中に特に強い光の色（波長）があれば，我々は，その方向の光はその色に見えます。

　では光の強さは何で決まるか？　それは光のエネルギー密度……ということになりますが，これを光線の本数の多い少ないでイメージするならば，光線の詰まり具合，すなわち光線密度の大小で決まる……といえます。

　太陽光線は雨滴に満遍なく均等に入射してきます。この段階では，光線密度に差はありません。しかし雨滴で散乱されると，散乱角によって光線密度にばらつきが出てきます。一定の射出角に含まれる光線数が多ければ明るい，少なければ暗い……というわけです。

　上図のように，衝突係数 $\varDelta y$ の幅に入射した光線が散乱角 $\Delta \theta$ の角度幅に散乱されたとすれば，同じ $\varDelta \theta$ に対して $\varDelta y$ が大きいほど $\varDelta \theta$ 内に多くの光線が含まれていることになり，光線密度は大きい。つまり，光線密度は $\varDelta y/\varDelta \theta$ に比例するといえます。

　上図は，前ページ $\maru{4}$ 式， $\maru{5}$ 式に基づく衝突係数 $y$ －散乱角 $\theta$ の関係図です（詳細は解説３参照）。
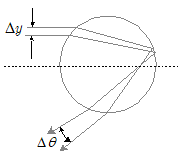
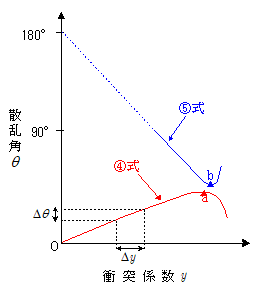
　ここで$\varDelta y/\varDelta \theta$ は，グラフの勾配 $\varDelta \theta/\varDelta y$ の逆数になっていることに注意してください。
　上図において，散乱角 $\theta$ は極値を持っており， $\maru{4}$ 式は点ａで極大値， $\maru{5}$ 式は点ｂで極小値をとります。すなわちこの部分では，衝突係数 $y$ の値が少しずれても散乱角 $\theta$ にほとんど変化がなく，光線が小さい散乱角の間に密集していることになります。数学的には，この位置で $\varDelta \theta/\varDelta y=0$ ，よってその逆数である $\varDelta y/\varDelta \theta$ の値は無限大に発散しており，光線密度は他の部分より極端に大きく，光強度が極めて強くなっていると言えます。すなわち，散乱角が極大値，極小値をとる角度方向で光が最も強いということが言えます。
　この散乱角の極大値，極小値が屈折率の関数になっていて，値が波長（色）によってわずかずつずれているために，角度によって違った色の光が目に入ることになり，これが虹として見える……というわけです。

次の解説，「解説３（散乱角の詳細計算）」　で，散乱角の極大値，極小値を求めます。

---

　　虹の話 　　概要
　　解説１（解説１：雨滴による虹散乱）
　　解説２（虹の色と散乱角）
　　解説３（散乱角の詳細計算）
　　解説４（反射率）
　　解説５（虹散乱での反射率）
　　　＊＊＊　以下，過剰虹　関連　＊＊＊　
　　解説６（波動光学）
　　解説７（過剰虹成因の概要）
　　解説８（波面の式）
　　解説９（虹の光強度の式）
　　解説１０（波動光学による虹）