過剰虹の詳細を求めることは簡単ではありませんが,いくつかの仮定のもとに近似な解析はできます。『光の気象学』(柴田清孝著。1999年 朝倉書店)に,詳細が紹介されています。本稿も,主に本書を参考にさせていただきました。
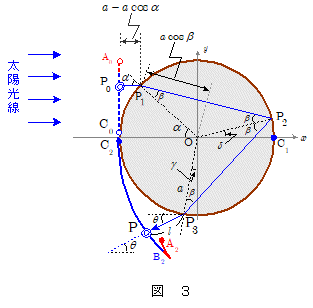
上の図3は,雨滴球の上半分に入射した波面 $\mathrm{A_0C_0}$ が雨滴内を通過後,波面全体が雨滴の外に出てきたときの波面 $\mathrm{A_2B_2C_2}$ となった瞬間の図です。その波面 $\mathrm{A_2B_2C_2}$ の式がどのようなものになるかについて考えていきます。
波面とは同位相面のことですから, $\mathrm{A_2B_2C_2}$ 上ではすべての点の位相が同じになっています。入射波面 $\mathrm{A_0C_0}$ 上でもすべての点で同位相でしたから,波面 $\mathrm{A_0C_0}$ から波面 $\mathrm{A_2B_2C_2}$ に至るまでの光学的距離(=屈折率×幾何距離)はどの点でも等しいことになります。まず,このことを立式してみましょう。
雨滴の半径を $a$ ,雨滴の屈折率を $n$ とすると,雨滴の中心線に沿って入射した光波が $\mathrm{C_0}\rightarrow \mathrm{C_1}\rightarrow \mathrm{C_2}$ と進んだときの往復距離は $2a \times 2 = 4a$ ,よってその光学的距離は $n \times 4a$ です。
また,入射波面 $\mathrm{A_0C_0}$ 上の1点 $\mathrm{P_0}$ (図3の◎印の点)から発し,雨滴球に入射角 $\alpha$ ,屈折角 $\beta$ で入射した光波が波面 $\mathrm{A_2B_2C_2}$ 上の点P(◎印)に達したとすると,その光学的距離 は,図の $\mathrm{P_3P}$ 間の距離を $l$ , 空気の屈折率を $1$ として,
\[ 1 \times \overline{\mathrm{P_0P_1}} + n \times ( \overline{\mathrm{P_1P_2}} + \overline{\mathrm{P_2P_3}}) + 1 \times \overline{\mathrm{P_3P}} \\ \kern-1em = 1 \times a(1 - \cos\alpha) + n \times a \cos\beta \times 4 + 1 \times l \]
となります。この光学距離が雨滴中心線に沿って入射した光線の光学的距離 $4na$ に等しいとおいて,
\[ 1 \times a(1 - \cos\alpha) + 4 n a \cos\beta + 1 \times l = 4 n a \\ \therefore l = a \{4 n ( 1 - \cos\beta) - (1- \cos\alpha ) \} \quad\cdots\maru{1} \]

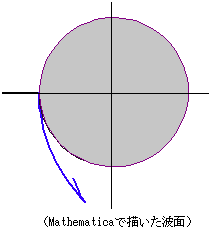
点Pを通る光線の 散乱角 $\theta$ ( 解説1の $\maru{1}$ 式参照)は, \[\color{red}{\theta = 4\beta -2\alpha } \] また図3における角度 $\gamma$ は,△ $\mathrm{OP_2P_3}$ において, \[ \gamma = \angle \mathrm{P_2OP_3} - \angle \mathrm{P_2OC_1} - \pi/2 \\ \quad\quad = (\pi - 2\beta) - \delta - \pi/2 \\ \quad\quad = (\pi - 2\beta) - \{ \pi -\alpha-(\pi-2\beta) \, \} - \pi/2 \\ \quad\quad = \pi/2 + \alpha - 4\beta \] したがって点Pの $x$ 座標, $y$ 座標は, \[x = -a \sin\gamma -l \cos\theta \\ \quad = -a \sin( \bun{\pi}{2} + \alpha -4\beta) -l \cos \theta \\ \quad = -a \cos( \alpha - 4\beta) -l \cos \theta \\ \quad = -a \cos( 4\beta - \alpha ) -l \cos \theta\quad\quad (\leftarrow ここで \theta を代入 )\\ \quad = - a \cos( \theta + \alpha) -l \cos \theta \quad\cdots\maru{2}\\ y = -a \cos\gamma - l \sin\theta \\ \quad = -a \cos ( \bun{\pi}{2} + \alpha -4\beta) - l \sin\theta \\ \quad = - a \sin (4\beta - \alpha) - l \sin\theta \\ \quad = - a \sin (\theta + \alpha) - l \sin\theta \quad\cdots\maru{3} \] 衝突係数(=光線の入射の高さ/雨滴球の半径)を $\eta$ とすると,入射角 $\alpha$ ,散乱角 $\theta$ は次式で与えられました(解説2 $\maru{4}$ 式 を参照)。(解説2では,衝突係数として $y$ の文字を用いたが,本項では $y$ の文字は座標として使用した。) \[\alpha = \arcsin(\eta) \\ \theta = 4\arcsin\bigg ( \bun{\eta}{n}\bigg) - 2\arcsin(\eta) \] $\maru{1}$ 式の $l$ を $\maru{2}$ 式, $\maru{3}$ 式に代入し,さらにこれに上記の $\alpha$ , $\theta$ を代入することによって, $x$ , $y$ を衝突係数 $\eta$ の関数として表すことができます。その $x$ , $y$ で表される面が,波面 $\mathrm{A_2B_2C_2}$ の式,ということになります。ちなみに下図は,上記 $x$ , $y$ で表される面を数学ソフト(Mathematica)で描図したもので,折れ曲がった部分まで含めて波面が完全に再現されています。
◎波面の式の書き換え:
しかし,光の強さの方向による違い-光強度分布-を求めようとするとき, $\maru{2}$ 式, $\maru{3}$ 式で与えられる $x$ , $y$ をこのまま使って計算するのには式があまりに複雑すぎて,扱いづらい。
そこで $\maru{2}$ 式, $\maru{3}$ 式に対して,デカルト光近傍の光線に限定した場合に成り立つくつかの近似を適用したり,座標軸の回転や原点移動,…といった処理を行うことによって, $\maru{2}$ 式, $\maru{3}$ 式に比べればはるかに単純な形の代替式を導き,この式を使って光の強度計算をすることが可能となります。この間の式変形等の詳細は,前述の書籍等を参照してください。
下図4において,破線で示した波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ は,上記の処理によって導かれる代替式によって示される波面を表します。この波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ は,光波の強度を計算する上で波面 $\mathrm{A_2B_2C_2}$ と等価の内容を持つ便宜上の波面であって,実際にこのような形の波面となる瞬間があるわけではありません。
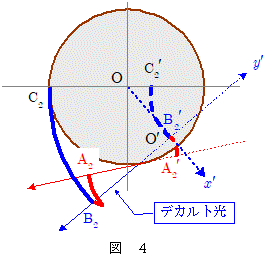
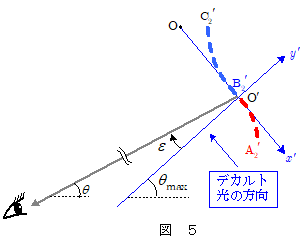
ここで図4のように,雨滴球の中心Oからデカルト光に垂線を下した交点 $\mathrm{O}{}'$ を原点とし, $\mathrm{OO{}'}$ の方向を $x'$ 軸に,デカルト光の方向を $y'$ 軸に選ぶと,便宜上の波面 $\mathrm{A_2{}'B_2{}'C_2{}'}$ は,原点 $\mathrm{O'}$ の近傍においては $x'$ の3次曲線として近似でき,以下の $\maru{4}$ 式のように簡単化できます(前述の書籍等を参照)。 \[ y' = -\bun{h}{3a^2}x{}'{}^3 \quad\quad\cdots\maru{4} \\ \kern-1em ただし,\quad h=\bun{9}{4(n^2 - 1)}\kon{\bun{4 - n^2}{n^2 - 1}} \] 以下の項で,この簡単化された $\maru{4}$ 式をもとに,デカルト光の方向と角 $\varepsilon$ をなす方向に進む光の強さを求めていきます。
解説9(過剰虹の方向と強さ)
虹の話
概要
解説1(解説1:雨滴による虹散乱)
解説2(虹の色と散乱角)
解説3(散乱角の詳細計算)
解説4(反射率)
解説5(虹散乱での反射率)
*** 以下,過剰虹 関連 ***
解説6(波動光学)
解説7(過剰虹成因の概要)
解説8(波面の式)
解説9(虹の光強度の式)
解説10(波動光学による虹)