平面波としての入射波,反射波,屈折波を数式化することを考えます。
( 注:『 2次元平面波について 』 を参照してください。)
◎入射波,反射波,屈折波の式:
再び図1のように,媒質 $\mathrm{I}$ から振動数が $f$ の平面波が入射角 $\theta_1$ で入射した場合を考えます。
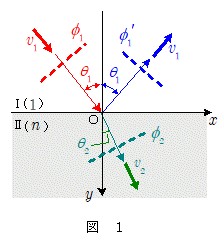
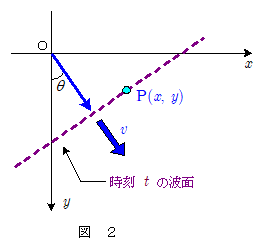
原点Oの時刻 $t$ における入射波による変位 $\phi_1(0,\,0,\,t)$ が,振幅を $A\,(\, > \, 0\,)$ として,\[\phi_1(0, \, 0,\, t)=A\sin(2\pi \, f \,t ) \]であるとすれば,点 $\mathrm{P}(x,\,y)$ での入射波,反射波,屈折波の時刻 $t$ における変位,$\phi_1(x, \, y, \, t)$ ,$\phi_1{}'(x, \, y, \, t)$ ,$\phi_2(x, \, y, \, t)$ は,反射波,屈折波の振幅を $B$ , $C$ として,次のように表されます。ただし,位相が $\pi$ ずれる可能性があることも考慮して, $B$ , $C$ は負の値もとり得るとします。\[\kern-2em \phi_1(x, \, y, \, t) = A\sin 2\pi \, f \,\bigg(t -\bun{x\sin\theta_1 + y\cos\theta_1}{v_1} \bigg ) \quad\cdots\cdots\maru{6} \\ \kern-2em \phi_1{}'(x, \, y, \, t) = B\sin 2\pi \, f \,\bigg(t -\bun{x\sin\theta_1 - y\cos\theta_1}{v_1} \bigg ) \quad\cdots\cdots\maru{7} \\ \kern-2em \phi_2(x, \, y, \, t) = C\sin 2\pi \, f \,\bigg(t -\bun{x\sin\theta_2 + y\cos\theta_2}{v_2} \bigg ) \quad\cdots\cdots\maru{8} \] 反射波 $\maru{7}$ については,入射波と比べて $y$ 軸方向の進行方向だけが逆になっていることから,前 $\maru{5}$ 式において $w_y$ の符号を替えて, $w_y = - \,\bun{v}{\cos\theta}$ を適用したものと考えれば理解できるでしょう。
◎振幅反射率,振幅透過率:
波が屈折率の異なる媒質の境界に入射したとき,物理的には,境界面上において次の2点が満たされているはずです。
$\mathrm{i}$ . 入射側と屈折側で変位が同じになっていること。
$\mathrm{ii}$ . 波が伝播していく方向について,入射側と屈折側で変位の傾きが同じになっていること。
の2点です。
その理由は,弦のような1次元の媒質で考えるとわかりやすいでしょう。
太さの異なる2本の弦が「つなぎ目」で接続されて,水平に張られているとします。その一方の端を上下にゆすって振動させたとき,2本の弦のつなぎ目では,左の弦と右の弦とで変位は常に同じになっています。なぜなら,もし等しくないとすれば,2本の弦はつなぎ目で切れていることになるからです。これが条件( $\mathrm{i}$ )です。
さらにつなぎ目において,弦の曲がり具合,つまり変位の傾きも左と右で同じになっています。もしそうでないとすると,2本の弦はそのつなぎ目でカックンと不連続に折れ曲がっていることとになり,つなぎ目という1点にかかる弦方向の力の大きさがつなぎ目の左側と右側とで一致しないことになるからです。これが条件( $\mathrm{ii}$ )です。
平面波の場合も同様です。媒質 $\mathrm{I}$ には入射波と反射波が存在し,媒質 $\mathrm{II}$ には屈折波が存在しますので,媒質 $\mathrm{I}$ 側では入射波と反射波の合成波 $\phi_1 + \phi_1{}'$ について,媒質 $\mathrm{II}$ では屈折波 $\phi_2$ について,境界線上,つまり $x$ 軸上のすべての点において常に条件 ( $\mathrm{i}$ ) と ( $\mathrm{ii}$ ) が満たされていなければなりません。
$x$ 軸上のすべての点において…ということですから,原点について考えていきましょう。
まず,条件 ($\mathrm{i}$ ) について考えます。 $\maru{6} \sim \maru{8}$ 式に $x = 0$ , $y = 0$ を代入して,\[\phi_1(0, \, 0,\, t) + \phi_1{}'(0, \, 0,\, t) = \phi_2(0, \, 0,\, t) \\ \kern-1em \therefore A\sin 2\pi \, f \,\bigg(t -\bun{ 0}{v_1} \bigg ) + B\sin 2\pi \, f \,\bigg(t -\bun{0}{v_1} \bigg ) = C\sin 2\pi \, f \,\bigg(t -\bun{0 }{v_2} \bigg ) \\ \kern-1em \therefore A + B = C \quad\cdots\cdots\maru{9} \] つぎに条件 ($\mathrm{ii}$ ) について考えます。 波は媒質 $\mathrm{I}$ から媒質 $\mathrm{II}$ の方に $y$ 軸方向に伝播していきますので,変位の傾きは $y$ 軸方向に連続していなければなりません。
変位の $y$ 軸方向の傾きは $\bun{\partial \phi}{\partial y}$ で与えられます。ここで $\bun{\partial \phi}{\partial y}$ は $ \phi$ を $y$ で微分するという意味の記号です。例えば $\maru{6}$ 式を $y$ で微分すると,\[\kern-2em \bun{\partial }{\partial y}\big\{\phi_1(x, \, y,\, t)\big\} = - \bun{2\pi \, f \cos\theta_1}{v_1}A \cos 2\pi \, f \,\bigg(t -\bun{x\sin\theta_1 + y\cos\theta_1}{v_1} \bigg ) \] のようになります。よって原点において条件 ($\mathrm{ii}$ ) を立式すると,\[\bun{\partial}{\partial y}\big\{\phi_1(0, \, 0,\, t) + \phi_1{}'(0, \, 0,\, t)\big\} = \bun{\partial}{\partial y}\big\{\phi_2(0, \, 0,\, t) \big\} \\ \kern-1em \therefore \bun{2 \pi f}{v_1} \cos\theta_1\cdot ( - A + B )\cdot \cos 2\pi \, f \,\bigg(t -\bun{0}{v_1} \bigg ) \\ \kern 10em = -\bun{2 \pi f}{v_2} \cos\theta_2 \cdot C\cdot \cos 2\pi \, f \,\bigg(t -\bun{ 0}{v_2} \bigg ) \\ \kern-1em \therefore \bun{\cos\theta_1}{v_1}\cdot ( - A + B ) = - \bun{\cos\theta_2}{v_2}\cdot C \\ \kern-1em \therefore ( A - B ) \cos\theta_1 = \bun{v_1}{v_2} \cos\theta_2 \cdot C \\ \kern-1em \therefore ( A - B ) \cos\theta_1 = n \cdot C\cdot \cos\theta_2 \quad\cdots\cdots\Maru{10} \] ただし屈折の法則の $\maru{2}$ 式 $n=v_1/v_2$ を適用した。$\maru{9}$ 式と $\Maru{10}$ 式とを連立させると,\[B = \bun{\cos\theta_1 - n\cdot \cos\theta_2}{\cos\theta_1 + n\cdot\cos\theta_2} \, A \\ C = \bun{2 \cos\theta_1 }{\cos\theta_1 + n\cdot\cos\theta_2} \, A \] となります。ここで $r = \bun{B}{A}$ を振幅反射率, $t = \bun{C}{A}$ を振幅透過率と定義し,さらに屈折の法則 $\maru{1}$ 式 $\sin\theta_2 = \bun{\sin\theta_1}{n}$ を適用すると,\[ r = \bun{B}{A} \\ \quad = \color{red}{\bun{\cos\theta_1 - n\cdot \cos\theta_2}{\cos\theta_1 + n\cdot\cos\theta_2} \quad \cdots\cdots\Maru{11}} \\ \quad = \bun{\cos\theta_1 - n\kon{1 - \bigg(\bun{\sin\theta_1}{n}\bigg)^2}}{\cos\theta_1 + n\kon{1 - \bigg(\bun{\sin\theta_1}{n}\bigg)^2}} \\ \quad = \color{red}{\bun{\cos\theta_1 - \kon{n^2 - \sin^2\theta_1}}{\cos\theta_1 + \kon{n^2 - \sin^2\theta_1}} \quad \cdots\cdots\Maru{11}' }\\ t = \bun{C}{A} \\ \quad = \color{red}{\bun{2 \cos\theta_1 }{\cos\theta_1 + n\cdot\cos\theta_2} \quad \cdots\cdots\Maru{12}} \\ \quad = \bun{2 \cos\theta_1 }{\cos\theta_1 + n\kon{1 - \bigg(\bun{\sin\theta_1}{n}\bigg)^2}} \\ \quad = \color{red}{ \bun{2 \cos\theta_1 }{\cos\theta_1 + \kon{n^2 - \sin^2\theta_1}} \cdots\cdots\Maru{12}'} \] もちろんこの場合,屈折波が生じる条件 $\maru{3}$ 式 $\sin\theta_1 \le n$ が満たされている必要があります。
(参考.上記の関係式は,光波(電磁波)のs波(振動方向が入射面に垂直方向の光波)に関するフレネルの式 $\maru{7} $ 式と同じになっています。)
$\Maru{12}'$ 式より,振幅透過率 $t$ は入射角 $\theta_1$ によらず $t \gt 0$ であり,透過波は常に入射波と同位相であることを意味します。
これに対して$\Maru{11}'$ 式より,振幅反射率 $r$ は,屈折率 $n$ および入射角 $\theta_1$ の値によって正の場合も負の場合もあります
・ $n \gt 1$ の場合 $r \lt 0$ となり,反射波の位相は入射波に対して $\pi$ ずれる のに対し,
・ $n \lt 1$ の場合 $r \gt 0$ となり,反射波は入射波と同位相 となります(もちろんこの場合,臨界角以上の入射角では屈折波は存在しない)。
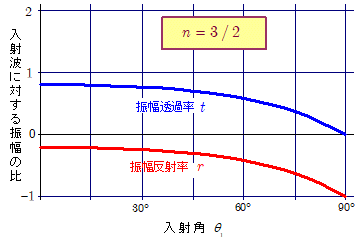
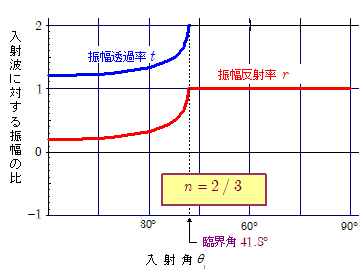
下図は, $n \gt 1$ の場合と $n \lt 1$ の場合について,それぞれ入射角 $\theta_1$ に対する振幅反射率 $r$ と振幅透過率 $t$ の関係を表すグラフです。
<参考> エネルギー反射率・エネルギー透過率 に続く。
シミュレーションへ戻る
解説 1(平面波の反射)
解説 2(全反射)
解説 4(エネルギー反射率・エネルギー透過率)
参 考 (数式による平面波の干渉)